26 Вынужденные колебания. Резонанс.

Вынужденные колебания затухающего осциллятора описываются уравнением

,

где  — периодическая внешняя (вынуждающая) сила. В простейшем случае синусоидальная сила

.

Подставим эту формулу в уравнение и разделим обе части на

,

где .

Решение этого дифференциального уравнения состоит из двух частей: решения уравнения без правой части, то есть уравнения затухающих колебаний и частного установившегося решения с частотой вынуждающей силы. Второй член выглядит следующим образом

.

Подстановка этого решения в уравнение позволяет найти формулы для амплитуды и фазы:

,

.

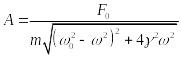То есть при изменении частоты вынуждающей силы меняется установившаяся амплитуда и сдвиг фаз между колебаниями  и . График амплитуды

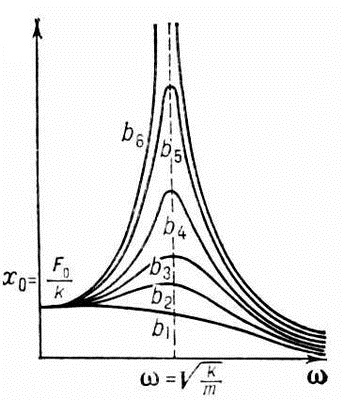
представлен на рисунке. Разные кривые соответствуют разным значениям  (на рисунке ). Очевидно, что кривые имеют максимум. Положение максимума при резонансной частоте .

 

27 Волновые процессы. Уравнение плоской волны. Дифференциальное уравнение плоской волны.

Процесс распространения в пространстве колебаний любой физической величины называется волновым движением или волной.

Если направление распространения и направление колебаний совпадают, то волна называется продольной. Если эти направления взаимно перпендикулярны, то волна называется поперечной.

Существует много типов волн. Мы рассмотрим только гармонические волны. Колеблющаяся величина в случае плоской волны вдоль оси  представляется в виде:

,

где  — волновое число. Остальные уже известны. Если продифференцировать частным образом по времени и координате эту формулу и сравнить полученные результаты, то можно вывести дифференциальное уравнение плоской бегущей волны

,

где  — скорость распространения волны. В случае трехмерного волнового движения уравнение следующее:

.

Скорость распространения волны разная для разных волновых процессов. В случае электромагнитных волн она равна скорости света, для упругих колебаний в различных средах — скорости звука в данной среде.

 

 

28 Макроскопическая система большого количества молекул. Ее параметры. Равновесная система.

 

29 Массы и размеры молекул. Атомная масса. Молярная масса.

Так как массы атомов и молекул очень малы, то обычно они измеряются не в кг, а с помощью специальной единицы, называемой относительной атомной массой (сокращенно — атомной массой).

Атомной массой называется отношение массы атома к атомной единице массы, равной 1/12 массы атома изотопа углерода (углерода-12) (Атомная единица масс равна ). Аналогично определяется и молекулярная масса.

Для характеристики количества вещества используют понятие моля. Моль — это такое количество вещества, которое содержит столько же структурных элементов (частиц), сколько атомов содержится в 12 г углерода-12. Это число называется числом Авогадро и равно .Масса одного моля  называется молярной массой и измеряется г/моль или кг/кмоль. Масса 1 молекулы вещества равна

.

Экспериментальная оценка поперечных размеров молекулы для неорганических веществ имеет порядок .