1 Кинематика материальной точки. Тело отсчета. Прямолинейное движение. Движение тела в пространстве. Декартова система координат. Система отсчета.

      Тело отсчета — тело, относительно которого задается система отсчета.

Простейшим объектом в механике является материальная точка – макроскопическое тело, размерами которого можно пренебречь при рассмотрении данного движения. Математически материальная точка эквивалентна математической точке, у которой есть одно физическое свойство – масса. Но тело должно оставаться макроскопическим. Иначе материальная точка может стать меньше молекулы. А движение  молекул классической механикой не описывается.

Если тело не может быть рассмотрено как материальная точка, то можно рассмотреть два случая. Более простой – когда расстояния между материальными точками, составляющими тело, не меняются во времени. Тогда тело называют абсолютно твердым телом, или просто твердым телом. Движения материальной точки и твердого тела могут быть рассмотрены в классической механике.

Начнем с материальной точки (МТ). Описание движения МТ сводится к нахождению трех координат как функций времени:

или к нахождению одной векторной функции

Для того, чтобы сформулировать законы механики, необходимо ввести два новых понятия: понятие скорости и понятие ускорения.

Прямолинейное движение

 

Рассмотрим частный случай, когда материальная точка движется по прямой линии. Примем эту прямую за координатную ось , поместив начало координат  в произвольной ее точке. Положение МТ определяется одной координатой . Пусть в какой-то момент времени  координата МТ равна . В более поздний момент ее координата равна . За время  МТ испытывает перемещение . Отношение  к   называется средней скоростью МТ  за время между  и :

 

Начнем уменьшать величину , и соответственно будет уменьшаться . Тогда их отношение будет стремится к величине называемой мгновенной скоростью МТ в момент времени .

В математике такая величина называется производной функции  по аргументу .

 

Скорость МТ является функцией времени . Производная скорости по времени называется ускорением МТ. Ускорение обозначается через .

Ускорение также является второй производной координаты по времени и обозначается

Декартова система координат

В качестве пространственной системы отсчета можно взять произвольное твердое тело и связать с ним координатные оси, например, декартовой прямоугольной системы координат. Положение каждой точки в избранной системе отсчета можно задавать тремя числами: , представляющие собой расстояния от этой точки до координатных плоскостей  соответственно (рис. 1).  Координаты можно объединить в радиус-вектор , проведенный из начала координат в рассматриваемую точку:

где — координатные орты, т.е. единичные векторы вдоль координатных осей

 

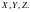
2 Радиус-вектор, скорость и ускорение материальной точки, их связь с декартовыми координатами.

 

Перейдем к криволинейному движению МТ. Положение движущейся точки на траектории задается радиус-вектором , проведенным в эту точку из начала координат . (остальное смотреть выше)