3. Расчет нагрузок цепной передачи.

1. Натяжение от провисания ведомой ветви от собственной массы (2. см. с. 41)

F_f= K_fqga = 4 * 1,0 * 9,81 * 0,635 = 2 Н,

где Kf= 4 — коэффициент провисания (2. см. с. 41);

a=60t=60*15.875= 952мм.

2.Натяжение от центробежных сил при скорости цепи у с 12 м/с не учитывается (2. см. с. 41).

3.Окружное усилие Ft= 2881.82 Н (вычислено выше).

4.Суммарное натяжение ведущей ветви (2. формула 2.47),

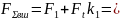25 + 2881.82 =2906.82 Н.

5.Нагрузка, действующая на валы (2. формула 2.50)

Проверяем цепь по запасу прочности (2. формула 2.54):

.

что меньше допускаемого [n] = 13,2 (2. табл. 2.30).

4. Геометрический расчет передачи.

1. Межосевое расстояние

а = 952 мм (вычислено выше).

2.Число зубьев ведомой звездочки

z₂= z₁u = 25 * 3 = 75.

3.Длина цепи, выраженная в шагах (2. формула 2.40),

.

Количество звеньев цепи округляем до четного числа Lt = 172, чтобы избежать применения переходного соединительного звена.

4. Действительное межосевое расстояние, соответствующее округленной длине Lt, не вычисляем, так как электродвигатель установлен на салазках.

5. Делительные окружности звездочек определяем по табл. 2.32:

ведущей

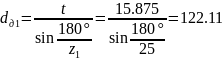мм.

ведомой

.

5. Расчёт зубчатой передачи:

N₁=3кВт.(номинальная мощность, передаваемая шестерней)

n1=955 мин^-1(частота вращения шестерни)

u=6.37(передаточное число редуктора)

t=10000 ч.(срок службы передачи)

передача нереверсивная

1.Выбор материала и допускаемых напряжений для шестерни и колеса. 1. По табл. 3.12 назначаем материал для шестерни и колеса — сталь 40ХН (поковка); термообработка — улучшение. Для шестерни при радиусе заготовки до 100 мм.

= 850 МПа; 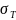= 600 МПа; 230 ... 300 НВ₁

для колеса при радиусе заготовки до 300 мм.

= 800 МПа; = 580 МПа; 24НВ₂.

2. Определяем допускаемое напряжение изгиба для шестерни (2. формула 3.51):

Предварительно находим предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений (2. формула 3.52):

где предел выносливости при изгибе, соответствующий базовому числу циклов перемены напряжений (2. табл. 3.19).

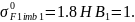8 * 265 = 477 МПа.

Коэффициент, учитывающий влияние двухстороннего приложения нагрузки (2. табл. 3.20), при одностороннем приложении нагрузки K_FC= 1,0; коэффициент долговечности (2. формула 3.53)

При HВ < 350 (см. с. 77) m_F= 6; базовое число циклов перемены напряжений (см, 2. с. 77)

N_FO = 4* 10⁶,

эквивалентное (суммарное) число циклов перемены напряжений (2. формула 3.54)

N_FE1=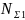 =60n₁t_Ч=60*955*10000=5.73*10⁸

Соответственно

но так как = > N_F0 = (2. см. с. 77), принимаем 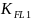=1.0 Соответственно 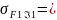477 *1,0* 1,0 = 477 МПа. Коэффициент безопасности (2. формула 3.56)

S_F=S^ᶦ_F* S^ᶦᶦ_F=

где S^ᶦ_F = 1,75 (2. табл. 3.19), S^ᶦᶦ_F = 1,0 (2. табл. 3.21). Коэффициент, учитывающий чувствительность материала к концентрации напряжений (2. формула 3.57), Y_S .== 1. Коэффициент, учитывающий шероховатость переходной поверхности зуба (2. формула 3.58), Y_R— 1,0.

Допускаемое напряжение изгиба для зубьев шестерни

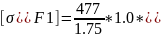1,0 = 272 МПа.

3. Допускаемое напряжение изгиба для зубьев колеса

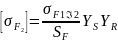
Предварительно находим предел выносливости зубьев при изгибе, соответствующий эквивалентному числу циклов перемены напряжений (2. формула 3.52):

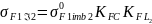
где предел выносливости при изгибе, соответствующий базовому числу циклов перемены напряжений (2. табл. 3.19),

= 1,8НВ₂ = 1,8 * 241 = 434 МПа.

Коэффициент, учитывающий влияние двухстороннего приложения нагрузки (2. табл. 3.20), K_FC= 1,0; коэффициент долговечности (2. формула 3.53)

При HB< 350 (см. с. 77) mF = 6; базовое число циклов перемены напряжений (2. см. с. 77) N_FO = 4 *10⁶; эквивалентное (суммарное) число циклов перемены напряжений (2. формула 3.54)

N_FE2= =60n₂t_Ч=60* *10000=0.9*10⁸

Соответственно

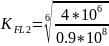
но так как N_FE2= 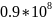>N_F0= (2. см. с. 77), принимаем = 1.0. Предел выносливости

= 434 * 1,0 * 1,0 = 434 МПа.

Коэффициент безопасности (2. формула 3.56) S_F =1,75.

Коэффициент, учитывающий чувствительность материала к концентрации напряжений (формула 3.57), Y_s= 1,0. Коэффициент, учитывающий шероховатость переходной поверхности зуба (формула 3.58), Y_R= 1,0. Допускаемое напряжение изгиба для колеса

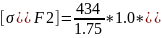1,0 = 248 МПа.

4. Допускаемое напряжение изгиба при расчете на действие максимальной нагрузки (2. формула 3.62) для шестерни

Предварительно находим предельное напряжение, не вызывающее остаточных деформаций или хрупкого излома зуба (2. табл. 3.19):

= 4,8 HB₁ = 4,8*265 = 1272 МПа;

коэффициент безопасности (2.см. с. 76)

S_FM1=S'_FM1S''_FM1=1,75*1,0=1,75,

здесьS'_FM1= 1,75 (2. см. с. 80); S``<sub>FM1</sub> = S``_F1= 1,0 (2. табл. 3.21). Коэффициент, учитывающий чувствительность материала к концентрации напряжений (2. формула 3.57), 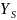= 1,0. Следовательно,

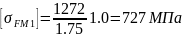
5.Допускаемое напряжение изгиба при действии максимальной нагрузки для колеса

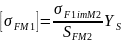
где предельное напряжение, не вызывающее остаточных деформаций или хрупкого излома зуба (табл. 3.19),

= 4,8H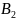 =4,8* 241 = 1157 МПа.

Коэффициент безопасности (см. с. 80)

SF М2 = S'F M2S''F М2 = 1,75 * 1,0 = 1,75,

здесь S'FM2= 1,75 (см. с. 80), S''FM2= S'F2= 1,0 (2. табл. 3.21).

Коэффициент, учитывающий чувствительность материала к концентрации напряжений, YS= 1,0. Следовательно,

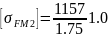= 661 МПа.

6.Допускаемое контактное напряжение для шестерни (2. формула 3.33)

Предварительно находим предел контактной выносливости поверхностей зубьев, соответствующий эквивалентному числу циклов перемены напряжений (формула 3.34):

= *

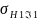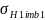здесь предел контактной выносливости, соответствующий базовому числу циклов перемены напряжений (2. табл. 3.17),

2Н + 70 = 2 * 265 + 70 = 600 МПа.

Коэффициент долговечности (2. формула 3.35)

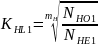
где базовое число циклов перемены напряжений (2. рис. 3.16)

N HOI = 1,8 * ;

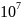эквивалентное (суммарное) число циклов перемены напряжений

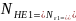60 =60 * 1000 * 10 000 =6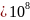

Отношение

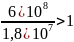= , поэтому коэффициент долговечности определяем по формуле (3.38):

0,9 т.е.,

=0,86

принимаем K_HLI = 0,9.

Предел контактной выносливости = 600 * 0,9 = 540 МПа.. Коэффициент безопасности для зубьев с однородной структурой материала (см. с. 75) SH1= 1,1. Коэффициент, учитывающий шероховатость сопряженных поверхностей (табл. 3.18), ZR= 0,95. Коэффициент, учитывающий окружную скорость (см. с. 75), ZV= 1,0. Допускаемое контактное напряжение для шестерни

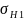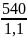[ ] = * 0,95 * 1,0= 466 МПа.

7. Допускаемое контактное напряжение для колеса

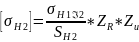
Предварительно находим предел контактной выносливости поверхностей зубьев, соответствующий эквивалентному числу циклов перемены напряжений:

=

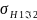где предел контактной выносливости, соответ­ствующий базовому числу циклов перемены напряжений (2. табл. 3.17),

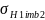= 2НВ₂ + 70 = 2 * 241 + 70 = 552 МПа;

коэффициент долговечности (формула 3.35)

здесь базовое число циклов перемены напряжений (рис.3.16) 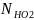=1,7*107; эквивалентное (суммарное) число циклов перемены напряжения

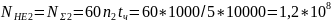
Отношение = 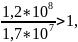коэффициент долговечности определяем по формуле (3.38)

,

.

Следовательно,

Коэффициент безопасности для зубьев с однородной структурой материала (см. с. 75) S_H2= 1,1. Коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев (табл. 3.18), ZR=0,95. Коэффициент учитывающий окружную скорость (см. с. 75),Z_R=1,0.

Допускаемое контактное напряжение для колеса

[ ] = 0,95 * 1,0 = 438 МПа.

8.Допускаемое контактное напряжение пе­редачи (2. формула 3.41)

[ ] = 0,45 ([ ] + [ ]) = 0,45 (466 + 438) = 408 МПа.

Проверяем условие (2. формула 3.42)

[ ] = 408 МПа < 1,23 [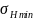 ] = 1,23* 438 = 539 МПа,

т. е. условие выполнено, поэтому принимаем допускаемое контактное напряжение передачи

[ ] = 408 МПа.

9. Допускаемое контактное напряжение при расчете на действие максимальной нагрузки (см. с. 80) для шестерни

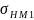[ ] = 2,8 = 2,8 * 600 = 1680 Мпа

Для колеса

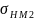[ ] = 2,8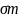 = 2,8 * 580 = 1624 Мпа

10. Расчет передачи на контактную вынос­ливость. Вычисляем начальный диаметр шес­терни (2. табл. 3.13, формула 3.16)

.

Предварительно определяем величины, необхо­димые для расчета. Номинальный крутящий момент на шестерне (формула 3.12)

Т_H1=9550*10³*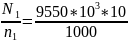 = 95 500 Н * мм.

Ориентировочная окружная скорость (форму­ла 3.27)

,

При данной скорости требуемая степень точ­ности зубчатых колес (табл. 3.33) — 9-я. Коэф­фициент, учитывающий распределение нагрузки между зубьями (рис. 3.13),Кнα= 1,13. Коэф­фициент ширины зубчатого венца при симмет­ричном расположении опор (2. табл. 3.15)

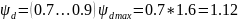
Проверяем условие (3.26) 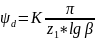. При­нимаем (см. с. 71) К = 2; угол наклона (см. с. 60)

β= 16°; минимальное число зубьев шес­терни (2. табл. 3.3) z_1min— 16; расчетное число зубьев шестерни (см. с. 58) z₁= z_1min+2 =16+2=18.

Соответственно

.

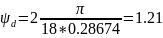Коэффициент, учитывающий распределение на­грузки по ширине венца (рис. 3.14, б), К_Hβ =1,07. Коэффициент, учитывающий динамиче­скую нагрузку (табл. 3.16),K_Hυ= 1,038 (опре­деляется интерполированием). Коэффициент, учитывающий форму сопряженных поверхностей (формула 3.28'),

Z_H= 1,76cosβ = 1,76 cos16° = 1,69.

Коэффициент, учитывающий механические свой­ства материалов сопряженных колес (формула 3.29), Z_M= 275 . Коэффициент, учиты­вающий суммарную длину контактных линий (2. формула 3.31),

,

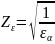где коэффициент торцового перекрытия (формула 3.3)

Соответственно

.

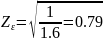Начальный диаметр шестерни

.

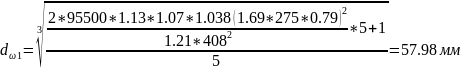Модуль зацепления (формула 3.46)

.

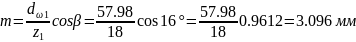Полученный модуль округляем до стандартного значения (см. приложение, табл. 9) m = 3 мм. По стандартному модулю m= 3 мм пересчитываем начальный диаметр

мм.

11. Проверочный расчет передачи на контактную выносливость. Определяем расчетную окружную скорость (2. формула 3.47) при начальном диаметре шестерни d_ω1=56,179 мм.

.

При данной скорости требуемая степень точности передачи (2. табл. 3.33) — 9-я, что соответствует принятой ранее степени точности. Уточняем по скорости υ = 2,94 м/с коэффициенты, входящие в формулу (3.48): К'_Hυ= 1,039 (табл. 3.16), К'_Hα = 1,15 (рис. 3.13), Z'_υ = 1,01 (2. рис. 3.17)

Уточняем начальный диаметр шестерни (2. формула 3.48):

.

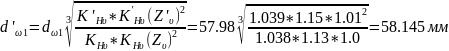По уточненному начальному диаметру d_ω1 находим модуль зацепления

.

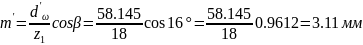Полученный модуль вновь округляем до стандартного значения m= 3 мм, что совпадает с ранее принятой величиной модуля; следовательно, диаметр начальной окружности шестерни d_ω1 = 56,179 мм. Ширина зубчатого венца при .

.

принимаем b_ω=70 мм.

12. Проверочный расчет зубьев на контактную прочность при действии максимальной нагрузки. Расчетное напряжение от максимальной нагрузки (2. формула 3.60)

,

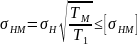где действующее напряжение при расчете на контактную выносливость (табл. 3.13, формула 3.15)

=

.

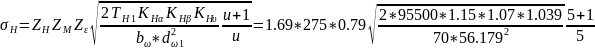Отклонение действующих контактных напряжений от допускаемых составляет 0,3 %, что допустимо. Расчетное контактное напряжение от максимальной нагрузки

.

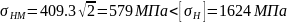где 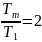задано в исходных данных расчета.

13. Проверочный расчет зубьев на выносливость по напряжениям изгиба. Расчетное напряжение изгиба (2. табл. 3.13, формула 3.17)

.

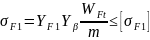Предварительно определяем величины, необходимые для расчета. Эквивалентное число зубьев шестерни и колеса (см. с. 76)

;

.

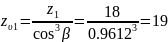Коэффициенты, учитывающие форму зуба шестерни и колеса (рис. 3.18), Y_F1= 4,13; Y_F2 = 3,6. Коэффициент, учитывающий влияние наклона зуба на его напряженное состояние (формула 3.50),

.

Расчетная удельная нагрузка (2. формула 3.25')

,

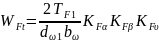где коэффициент, учитывающий распределение нагрузки между зубьям (2. формула 3,49),

.

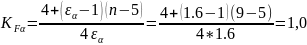Коэффициент, учитывающий распределение нагрузки по ширине венца (рис. 3.14, г), K_Fβ= 1,16; коэффициент, учитывающий динамическую нагрузку (табл. 3.16), K_Fυ= 1,1 (определяется интерполированием). Соответственно

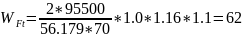Н/мм.

Напряжение изгиба в зубьях шестерни

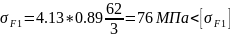=272 МПа,

в зубьях колеса (табл. 3.13, формула 3.17')

=248 МПа.

14. Проверочный расчет при изгибе максимальной нагрузкой. Расчетное напряжение от максимальной нагрузки (2. формула 3.61)

.

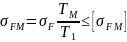Напряжения изгиба при расчете на выносливость:

для зубьев шестерни σ_F1=76 МПа.

для зубьев колеса σ_F2= 66 МПа.

Расчетное напряжение изгиба от максимальной нагрузки:

для зубьев шестерни

=727 МПа;

для зубьев колеса

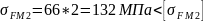=661 МПа.

15. Принимаем окончательно параметры передачи:

.

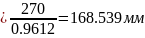Определяем межосевое расстояние

.

Проверяем межосевое расстояние

.

16. При необходимости округления межосевого расстояний до целого числа пересчитываем угол наклона β (формула 3.2'). Принимаем мёжосевое расстояние a_ω= 168 мм; соответственно угол наклона

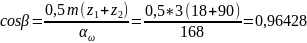
и β= .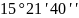

Пересчитываем начальные диаметры шестерни

,

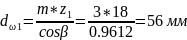колеса

.

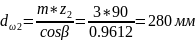Проверяем межосевое расстояние

.