5.2. Логарифмические частотные характеристики сау

При всей информативности АФХ, которая одновременно определяет изменения и амплитуды и фазы выходного сигнала САУ относительно входного для разных значений частот, пользоваться ею не всегда удобно. Для определения частотных характеристик САУ по отношению к сигналу заданной частоты  необходимо найти соответствующую этой частоте точку на графике АФХ и далее рассчитать А() и (). Удобнее анализировать отдельно зависимость усиления (ослабления) амплитуды на выходе САУ и сдвига фазы, вносимого САУ, от частоты входного сигнала.

Прологарифмируем левую и правую части выражения частотной передаточной функции :

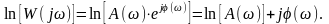
Логарифм частотной передаточной функции равен комплексному выражению, действительной частью которого является логарифм модуля (амплитуды), а мнимой – фаза.

Для практических целей удобнее пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудно-частотную L(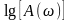) =  и логарифмическую фазочастотную () характеристики САУ или звена.

Поскольку логарифмическая амплитудно-частотная характеристика (ЛАЧХ) показывает усиление амплитуды выходного сигнала САУ относительно входного, ее величину принято измерять в децибелах – стандартная единица оценки соотношения двух величин. Бел представляет собой логарифмическую единицу, соответствующую десятикратному увеличению мощности. Один бел соответствует увеличению мощности в 10 раз, 2 бела – в 100 раз и т.д. Децибел равен одной десятой части бела. Если бы A(w) было отношением мощностей, то перед логарифмом в правой части формулы для перевода белов в децибелы должен был бы стоять множитель 10. Но А(w) представляет собой отношение не мощностей, а амплитуд выходной и входной величин. Увеличение этого отношения в десять раз будет соответствовать увеличению мощностей в сто раз, что соответствует двадцати децибелам. Поэтому в правой части формулы перевода L(w) в децибелы стоит множитель 20. Т.о., выражение для расчета ЛАЧХ в децибелах имеет вид:

.

(12)

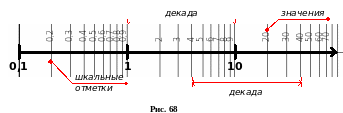
При построения ЛАЧХ и логарифмической фазочастотной характеристики (ЛФЧХ) по оси абсцисс откладывается частота в логарифмическом масштабе, т.е. нанесенные шкальные отметки соответствуют lg(), но около отметок записывается собственное значение частоты . Отрезок логарифмической шкалы, соответствующий увеличению частоты в десять раз (от 1 до 10; от 20 до 200 и т.д.), а значения ее логарифма – на единицу, называется декадой (Error: Reference source not found). По оси ординат откладывается значения ЛАЧХ в децибелах или значения ЛФЧХ в радианах или градусах. Для этой цели на ось ординат наносится равномерный масштаб.

Рассмотрим логарифмические частотные характеристики САУ, для которой ранее был рассмотрен пример построения АФХ. ЛАЧХ для этой САУ, рассчитанная по формуле (12), имеет вид, приведенный на Error: Reference source not found.

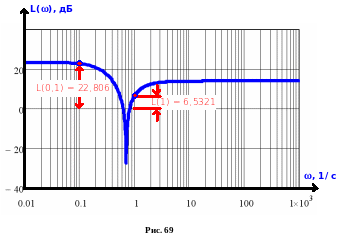
На графике (см. Error: Reference source not found) отмечены точки, соответствующие значениям частоты  = 0,1 и 1, для которых значения ЛАЧХ равны, соответственно:

L(0,1) = 22,806 дБ; L(1) = 6,5321 дБ.

Определим по значению ЛАЧХ с использованием формулы (12) усиление сигнала частоты 0,1:

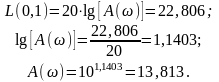
Полученное значение А() практически равно величине, определенной по результатам анализа АФХ рассматриваемой САУ (см. Error: Reference source not found), т.е. значение L(w) = 22,806 дБ соответствует усилению амплитуды входного сигнала на выходе САУ в 13,813 раз.

Аналогично, для частоты равной 1 (см. для сравнения Error: Reference source not found):

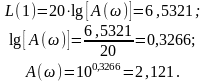
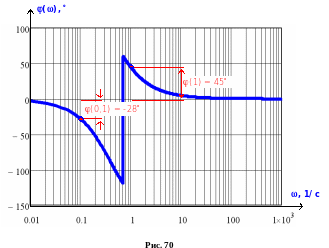
ЛФЧХ рассматриваемой САУ, рассчитанная с применением (11) и построенная с использованием логарифмического масштаба для оси частот, имеет вид, приведенный на Error: Reference source not found. Как видно, значения (w) для  = 0,1 и 1 совпадают со значениями, полученными ранее по результатам анализа АФХ (см. Error: Reference source not found и Error: Reference source not found).
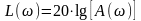