4.5. Дифференцирующие звенья

Идеальное дифференцирующее дает на выходе величину, пропорциональную производной входного сигнала, т.е. скорости изменения входного воздействия (см. Приложение 1):

,

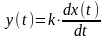где k – коэффициент статического преобразования (коэффициент усиления) идеального дифференцирующего звена. Передаточная функция звена имеет вид: .

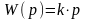Дифференцирующее звено реагирует не на изменение самой входной величины, а на изменение ее производной, то есть на тенденцию развития событий. Поэтому говорят, что дифференцирующее звено обладает упреждающим, прогнозирующим действием. С его помощью можно ускорить реакцию САУ на изменяющиеся входные воздействия.

Проанализируем форму переходной характеристики идеального дифференцирующего звена (см. Приложение 1). При подаче на вход звена единичной ступеньки x(t) = 0 для t < 0 и x(t) = 1 для t > 0. Производная постоянной величины равна нулю, следовательно, y(t) = 0 для t < 0 и для t > 0. И только в момент непосредственного изменения входного воздействия с нуля на единицу, т.е. в момент времени t = 0, производная входного сигнала dx(t)/dt не равна нулю:

.

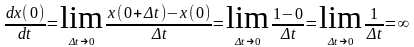В результате переходная характеристика идеального дифференцирующего звена в момент времени t = 0 теоретически имеет форму импульса с бесконечно большой амплитудой и бесконечно малой длительностью. Понятно, что такую переходную характеристику невозможно получить с использованием реального устройства САУ. Поэтому идеальное дифференцирующие звено, а также звенья этого типа первого и второго порядков (см. Приложение 1) являются модельными и относятся к физически нереализуемым звеньям.

Приближенно в качестве идеального дифференцирующего звена может рассматриваться операционный усилитель, включенный в режиме дифференцирования (Error: Reference source not found–а), и тахогенератор постоянного тока, если в качестве входной величины рассматривать угол поворота его ротора (t), а в качестве выходной – напряжение якоря U_я(t) (Error: Reference source not found–б).

ПРИМЕР переходной характеристики операционного усилителя в режиме дифференцирования.

В тахогенераторе постоянного тока при неизменном потоке возбуждения напряжение якоря можно считать пропорциональным угловой скорости вращения. В свою очередь скорость вращения есть производная от угла поворота:

,

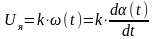что соответствует дифференциальному уравнению идеального дифференцирующего звена с коэффициентом статического преобразования k, y(t) = U_я(t); x(t) = (t).

Практически дифференцирующие устройства САУ вносят некоторое замедление в работу (обладают инерционностью), поэтому более точной моделью реальных устройств является дифференцирующее звено с замедлением, передаточная функция которого имеет вид:

,

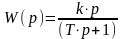т.е. представляет собой произведение передаточных функций идеального дифференцирующего звена и апериодического звена первого порядка. Т.о., дифференцирующее звено с замедлением можно представить последовательным соединением этих двух разновидностей типовых звеньев. Примерами дифференцирующего звена с замедлением могут служить трансформатор, емкостной дифференцирующий контур (Error: Reference source not found–а) и механическое дифференцирующее устройство, состоящее из пружины и демпфера (Error: Reference source not found–б).

Получим модель динамики емкостного дифференцирующего контура (см. Error: Reference source not found–а). Запишем уравнения входной и выходной цепей по закону Кирхгофа:

.

Продифференцируем уравнение входной цепи:

,

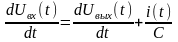и подставим в него ток i(t), выразив его из уравнения выходной цепи:

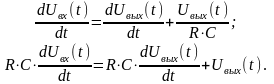
Выведем передаточную функцию емкостного дифференцирующего контура:

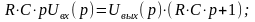
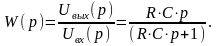
Полученная W(p) соответствует передаточной функции дифференцирующего звена с замедлением, у которого k = T = RC.

Получим модель динамики механического дифференцирующего устройства (см. Error: Reference source not found–б) для y(t) = s_вых(t); x(t) = s_вх(t) в предположении, что элемент трения (демпфер) и упругости (пружина) имеют нулевую массу. Уравнение движение демпфера для данного случая имеет вид:

,

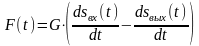где G – коэффициент сопротивления (демпфирования). Для пружины с коэффициентом упругости H уравнение движения имеет вид:

,

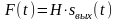следовательно, после подстановки:

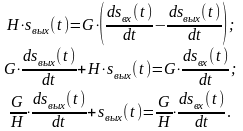
Выведем передаточную функцию механического дифференцирующего устройства:

Полученная W(p) соответствует передаточной функции дифференцирующего звена с замедлением, у которого k = T = G/H [1, 2, 7, 15].

ПРИМЕР переходной характеристики дифференцирующего звена с замедлением.