
- •Содержание
- •Конспект лекций
- •1. Введение в автоматическое управление технологическими системами
- •2. Основы автоматического управления
- •2.1. Принципы автоматического управления
- •2.1.1. Принцип разомкнутого управления (управление по задающему воздействию)
- •2.1.2. Принцип обратной связи (управление по отклонению)
- •2.1.3. Принцип компенсации (управление по возмущению)
- •2.1.4. Комбинированное управление
- •2.2. Классификация систем автоматического управления
- •2.2.1. По характеру изменения задающего воздействия (цели управления)
- •2.2.2. По принципу формирования сигналов управления
- •2.2.3. По числу контуров управления
- •2.2.4. По характеру зависимости управляемых переменных от входных воздействий
- •2.2.5. По характеру изменения ошибки управления
- •2.3. Моделирование и анализ систем автоматического управления
- •2.3.1. Модели статики и динамики сау
- •2.3.2. Модельные режимы анализа сау. Качество процесса управления
- •4. Типовые элементарные звенья систем автоматического управления
- •4.1. Усилительное безынерционное звено
- •4.2. Апериодическое звено первого порядка
- •4.3. Апериодическое звено второго порядка и колебательное устойчивое
- •4.4. Интегрирующие звенья
- •4.5. Дифференцирующие звенья
- •4.6. Безынерционное звено с чистым запаздыванием
- •4.7. Передаточные функции соединений звеньев. Преобразования структурных схем сау
- •5. Частотные характеристики систем автоматического управления
- •5.1. Частотная передаточная функция и амплитудно-фазовая характеристика сау
- •5.2. Логарифмические частотные характеристики сау
- •5.3. Асимптотическая лачх сау
- •6. Устойчивость систем автоматического управления
- •6.1. Теорема Ляпунова
- •6.2. Критерии устойчивости сау
- •6.2.1. Критерий Гурвица
- •6.2.2. Критерий Михайлова
- •6.2.3. Критерий Найквиста для афх
- •6.2.4. Критерий Найквиста для лачх и лфчх
- •6.3. Запасы устойчивости сау
- •Литература
- •Приложение 1. Типовые элементарные звенья
- •Приложение 2. Правила эквивалентных преобразований структурных схем
4.4. Интегрирующие звенья
Идеальным интегрирующим звеном называется такое звено, выходная величина которого пропорциональна интегралу по времени от входной величины (см. Приложение 1):
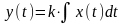
или
 ,
,
где k – коэффициент статического преобразования (коэффициент усиления) идеального интегрирующего звена, равный отношению скорости изменения выходной величины к входной.
Передаточная функция звена имеет вид:
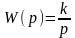 .
.
Переходная характеристика идеального интегрирующего звена имеет вид наклонной прямой, так как интеграл геометрически представляет собой площадь, ограничиваемую графиком ступенчатого входного воздействия x(t), которая возрастает с течением времени t. Решение дифференциального уравнения идеального интегрирующего звена имеет вид:
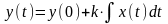 ,
,
откуда для единичной ступеньки (x(t) = 1 при t 0) при нулевых начальных условиях y(0) = 0 получаем линейно возрастающую переходную характеристику y(t) = kt. На Error: Reference source not found показаны переходные характеристики идеальных интегрирующих звеньев с различными значениями k.
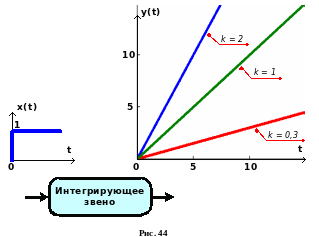
Простейший бытовой пример идеального интегрирующего звена – ванна, в которую набирается вода. Входное воздействие x(t) для этого объекта это приток (расход) воды через кран, а выходная величина y(t) – уровень воды в ванне. При поступлении воды уровень растет, т.е. система «накапливает» (интегрирует) входной сигнал.
Примерами идеальных интегрирующих звеньев являются такие устройства САУ, как операционный усилитель, используемый в режиме интегрирования (Error: Reference source not found–а) и гидравлический демпфер (Error: Reference source not found–б).
Уравнение операционного усилителя, используемого в режиме интегрирования, имеет вид:
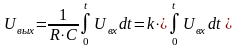 ,
,
что соответствует уравнению идеального интегрирующего звена, для которого k = 1/RC, Uвх = x(t), Uвых = y(t).
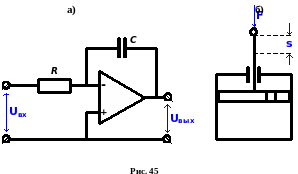
Для гидравлического демпфера входным воздействием является сила F, действующая на поршень, а выходной величиной – перемещение поршня s. Так как скорость движения поршня пропорциональна приложенной силе:
,
где G – коэффициент сопротивления (демпфирования), то перемещение поршня будет пропорционально интегралу от приложенной силы:
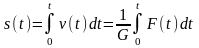 .
.
Полученное уравнение соответствует уравнению идеального интегрирующего звена, для которого k = 1/G, F(t) = x(t), s(t) = y(t).
Рассмотренная разновидность интегрирующих звеньев называется идеальной, т.к. его уравнение не учитывает инерционность описываемого звеном устройства САУ. В литературе этот тип звена иногда называют астатическим звеном.
Все реальные устройства вносят некоторое замедление в работу, поэтому более точной моделью реальных интегрирующих устройств является интегрирующее звено с замедлением, передаточная функция которого имеет вид:
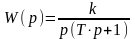 ,
,
т.е. представляет собой произведение передаточных функций идеального интегрирующего звена и апериодического звена первого порядка. Т.о., интегрирующее звено с замедлением можно представить последовательным соединением этих двух разновидностей типовых звеньев. Таким звеном может быть описан двигатель, если в качестве выходной величины рассматривать не угловую скорость, а угол поворота, являющийся интегралом от угловой скорости, а также демпфер, если более точно рассматривать его уравнение движения [1, 2, 7].
-
ПРИМЕР переходной характеристики интегрирующего звена
с замедлением.
