Свойства операций над множествами

(1) ) –

свойства коммутативности;

(2) ; (2') – свойства ассоциативности;

(3) ; (3) – свойства дистрибутивности;

( 4) ; (4) –

свойства идемпотентности;

( 5) ; (5') = –

законы де Моргана;

(6) ; (б') –

законы поглощения;

(7) = U; (7)  ;

( 8) AU=U; (8') А   ;

(9) А U = А; (9) А   А;

(7), (8), (9) – свойства пустого и универсального множеств;

(10) = – закон двойного отрицания;

(11) А\ (А\В) =А В – правило исключения разности.

Задачи.

1. Дайте словесное описание каждого из следующих множеств:

а) {x | х  R, x² +3x = 0}, б) {x | х  R, 5  x < 9}, в) {x | x  Z , x делится на 2 и х делится на 3}, г) {x | x  A или x  B}, д) {x | x  A и x  B},

е) {x³ | x — простое число}, ж) {x | x  A и x  B}.

2. Опишите каждое из следующих множеств, используя подходящее характеристическое свойство:

а) {1, 2, 3, 4, 5, 6, 7}; б) {4, 8, 12, 16, 20, 24}; в) {1, 4, 9, 16, 25, 36, …}; г) ;

д) {5, 8, 11, 14, 17}; е) {2, 3, 5, 7, 11, 13, 17, 19}.

3. Задайте перечислением элементов множества, определенные указанием характеристических свойств:

а) А = {x | x  N, x  7}; б) Б = {x | x  N, x < 0}; в) В = {x | x  Z, |x|  2}.

4. Какие из следующих множеств равны:

A = {1, 3, 5}, B = {1, 3, 3, 5}, C = {{1, 3}, 5}, D = {5, 3, 1}?

5. Найдите все подмножества

а) множества А = {а, в};

б) множества В = {5, 6, 7};

Ответьте на следующие вопросы:

в) сколько подмножеств имеет множество, состоящее из n элементов?

г) сколько подмножеств, содержащих нечетное число элементов, имеет множество, состоящее из n элементов?

6. а) Укажите виды правонарушений по степени общественной опасности и представьте множество правонарушений с помощью операций над выделенными подмножествами. Объединением каких подмножеств является множество проступков?

в) Опишите виды правонарушений по сферам общественной жизни и представьте множество всех правонарушений с помощью операций над его подмножествами еще одним способом.

7. Найдите объединение и пересечение двух множеств:

а) А = {x | x (4, 8)} и В = {x | x (1, 4]};

б) А = {x | x (3, 8)} и В = {x | x [5, 6]}.

8. Найдите следующие множества АВ, AB, А\В, В\А, если:

А = {1, 2, 4, 6, 9}, В = {3, 4, 5, 8, 9}.

9. Даны множества А = {0, 1, 2, 3, 4, 5, 6, 7}, B = {3, 4, 5, 6, 7, 8, 9},

C = { 3, 2, 1, 0, 1, 2, 3, 4}, D = {2, 3, 4, 5, 6}.

Найдите множества: 1) A  B  C  D; 2) A  B  C  D;

3) (А  В)  ( С  D); 4) (A  B)  (C  D).

10. В терминах теории множеств объясните загадку: два отца и два сына, а всего трое — как такое может быть?

11. Пусть А = {2n / n }, B = {2n + 1/ n }. Найдите множества: АВ, АВ, А \ В.

12. Пусть А – множество четных натуральных чисел, В – множество натуральных чисел, делящихся на 3, и С – множество натуральных чисел, делящихся на 5. Из каких чисел состоят множества А  В, В  С и А  В  С?

13. С помощью диаграмм Эйлера-Венна изобразите следующие множества:

а) , б) , в) , г) , д) , е) ,

ж) , з) , и) , к) .

Решение.

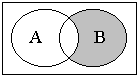
На диаграммах Эйлера-Венна будем изображать требуемое множество серым цветом, а множества, помогающие придти к ответу, – светло-серым цветом.

а) Сначала покажем множество (1), тогда искомым множеством (2) будет пересечение выделенного множества и множества В.

( 1) (2)

б ) Искомое множество выглядит следующим образом:

в) Вначале изобразим множества (), (), а затем ответ

( ) ()

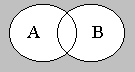
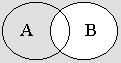14. С помощью диаграмм Эйлера-Венна изобразите следующие множества:

а) ; б) ; в) ;

г) ; д) ; е) .

15.С помощью диаграмм Эйлера – Венна изобразите следующие множества:

1. ; 17. ;

2. ; 18.

3. ; 19. ;

4. ; 20. ;

5. ; 21. ;

6. ; 22. ;

7. ; 23. ;

8. ; 24. ;

9. ; 25. ;

10. ; 26. ;

11. ; 27. ;

12. ; 28. ;

13. ; 29. ;

14. ; 30. ;

15. ; 31. ;

16. ; 32. .

16. Дано: . С помощью диаграмм Эйлера - Венна изобразите случаи, когда D и D

17. По данным диаграмм Эйлера-Венна определите, какое множество задано:

1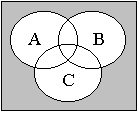 ) 2) 3)

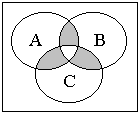
4) 5) 6)

18. Упростите следующие выражения:

1) А  (А  В); 2) (P  Q) (  P);

3) (А  В  )  ( А  В)  (В  С  );

4) (А  В)  ((А  В)  (  B)).

19. Докажите следующие тождества:

а) A  (B  C) = (A  B)  C; б) A  (B  C) = (A  B)  C;

в) A  (B  C) = (A  B)  (А  C); г) A  (B  C) = (A  B)  (А  C);

д) А \ ( B  C) = (А \ B)  (А \ C); e) А \ ( B  C) = (А \ B)  (А \ C);

ж) А \ (A\ B) = A  B; з) A  (B \ C) = (A  B) \ C.

Решение.

Обозначим множество, стоящее слева от знака равенства, через М, а стоящее справа от знака равенства, через N.

Для того, чтобы доказать тождество, нужно доказать, что каждый элемент множества М принадлежит множеству N, и наоборот.

а) Пусть произвольный элемент х  М , тогда х  А и х  В  С.

Следовательно, х  А и х  В, x  С. Тогда х  А  В и также x  С. Значит

x (A  B)  C, то есть x  N. Итак, мы показали, что множество М включается во множество N.

Покажем обратное.

Пусть х N, тогда х  А  В и x  С. Так как х  А  В, то х А и х  В. Так как x  С и х  В, то х  В  С, но х  А, и следовательно, х  A  (B  C), то есть х  М. Таким образом, множество N включается во множество М. Из включений следует равенство .

20. Верно ли, что

а) {1, 2}  {{1, 2, 3}, {1, 3}, 1, 2};

б) {1, 2}  {{1, 2, 3}, {1, 3}, 1, 2}?

21.Привести примеры таких множеств А, В, С, что

1) А  В, В  С и А  С ; 2) А  В, В  С, А  С;

3) А  В, А  В.

22. Для каких из следующих пар множеств имеет место одно из отношений А  В,

В  А, А = В, А  В, В  А?

1) А={a, b, c, d}, B={a, c, d}; 2) A=, B=;

3) A=, B = {a, b, c}; 4) A={a, b, c}, B = {b, c, a};

5) A=, B = {}; 6) A={{a}, a, }, B = {a};

7) A={{a, b}, {c, d}, c, d}, B = {{a, b}, c};

8) A= {{a}, a, 0}, B = .

23. Существуют ли множества А, В, и С, одновременно удовлетворяющие следующим условиям А  В  , А  С = , (А  В) \ С = ?