1.3 Кездейсоқ шаманың сандық сипаттамалары

Дискретті кездейсоқ шаманың математикалық үміті деп оның барлық мүмкін мәндерінің сәйкес ықтималдықтарына көбейтіндісінің қосындысын атайды.

, (5)

мұнда - кездейсоқ шама -тің мәндерінің саны.

Үздіксіз кездейсоқ шама үшін

. (6)

1 мысалдағы кездейсоқ шама үшін

.

Математикалық үміттің қасиеттері:

1) , мұнда С- тұрақты шама;

2)

3)

4) , мұнда - тұрақты шамалар;

5) Тәуелсіз кездейсоқ шамалар үшін .

кездейсоқ шаманың дисперсиясы деп кездейсоқ шаманың математикалық үміттен ауытқуының квадратының математикалық үмітін атайды.

Ықшамдалған формула

. (7)

Дискретті кездейсоқ шама үшін

. (8)

Үздіксіз кездейсоқ шама үшін

(9)

1 мысалдағы кездейсоқ шама үшін

Дисперсияның қасиеттері:

1)

2) тәуелсіз кездейсоқ шамалар болса,

3)

4) кез келген кездейсоқ шамалар болса,

Орташа квадраттық (сандартты) ауытқу деп, дисперсияның квадрат түбірінің арифметикалық мәнін атайды және былай белгілейді

(10)

1.4 Кездейсоқ шамалардың үлестіру заңдары

Көптеген кездейсоқ шамалардың үлестіру заңдарын білу арқылы олардың анықталған интервалда мән қабылдау ықтималдығын болжауға болады. Үлестіру заңдары өте көп. Біз тек қана экономикалық талдауда жиі кездесетін үлестіру заңдарын қарастырамыз. Оларға жататын: қалыпты үлестіру заңы, (хи - квадрат), Стьюдент, Фишер үлестірулері.

Қалыпты үлестіру. Үлестіру тығыздығы

(11)

түрінде берілген кездейсоқ шама қалыпты үлестірілген кездейсоқ шама деп аталады. Қалыпты үлестірудің үлестіру функциясы

(12)

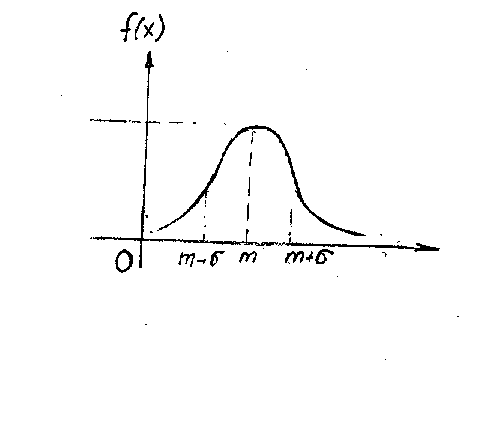Қалыпты үлестірілген кездейсоқ шаманың тығыздығы және үлестіру функциясының графиктері 4 және 5 суреттерде көрсетілген.

Сурет 4

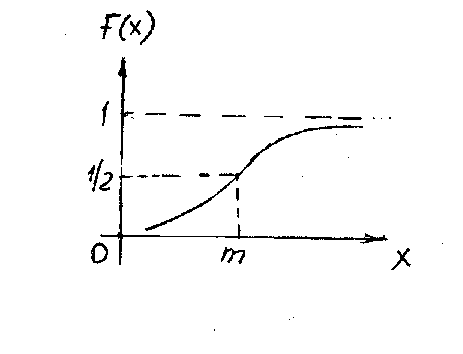
Сурет 5

(11) және (12) формулаларынан қалыпты үлестіру және σ параметрлерімен анықталады және олардан тәуелді

Егер қалыпты үлестірілген кездейсоқ шама болса, онда келесі символмен ~ , ~ деп жазуға болады. Қалыпты үлестірудің маңызды дербес жағдайы , стандартты қалыпты үлестіру деп аталады. Стандартты қалыпты үлестірілген кездейсоқ шама ~ деп белгіленеді.

(13)

Көп жағдайда практикалық есептеулерде мәндері кестемен берілген Лаплас функциясы қолданылады.

(14)

Бұл кестені кез келген қалыпты үлестірілген кездейсоқ шамалар үшін келесі ықтималдықтарды есептеуге пайдалануға болады

(15)

Егер

(хи - квадрат) үлестіруі. - тәуелсіз қалыпты үлестірілген кездейсоқ шамалар. және сәйкесінше математикалық үміттер, орташа квадраттық ауытқулар, яғни Онда , тәуелсіз қалыпты үлестірілген стандартты кездейсоқ шамалар болады, . Кездейсоқ шама , n еркіндік дәрежелі хи – квадрат үлестіруі болады, егер

(16)

Еркіндік дәрежесін деп белгілейміз, қосындылар құрамына кіретін кездейсоқ шамалар саны, ал кездейсоқ шамаларды байланыстыратын сызықтық теңдеулер саны. ( хи – квадрат) кездейсоқ шаманың еркіндік дәрежесі санымен анықталады. Олай болса, Хи – квадрат үлестіруінің математикалық үміті және дисперсиясы:

Егер және тәуелсіз үлестірілген еркіндік дәрежелері және кездейсоқ шамалар болса , онда олардың қосындысы да еркіндік дәрежесі -ға тең үлестірілген кездейсоқ шама болады. үлестіруі статистикалық болжамдарды тексеруде интервалдық бағаларды табу үшін қолданылады.

Стьюдент үлестіруі. Айталық кездейсоқ шама, ал V- еркіндік дәрежесі , - дан тәуелсіз үлестірілген кездейсоқ шама болсын. Онда

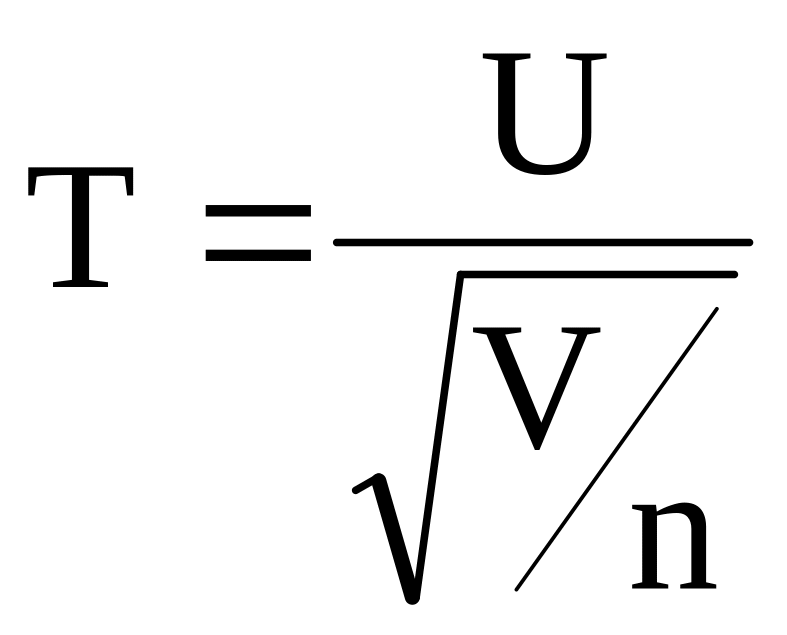(17)

еркіндік дәрежелі Стьюдент үлестіруі ( -үлестіруі ) деп аталады, яғни ( ~ ). (17) формуладан Стьюдент үлестіруі тек қана бір параметр, яғни еркіндік дәрежесімен анықталатынын көруге болады. Стьюдент үлестіруінің математикалық үміті және дисперсиясы:

Фишер үлестіруі. еркіндік дәрежелері және тәуелсіз үлестірілген кездейсоқ шамалар болса, онда шама

(18)

еркіндік дәрежелері және Фишер үлестіруі деп аталады. Олай болса, Фишер үлестіруі екі параметрмен анықталады, яғни және еркіндік дәрежелерімен. Стьюдент үлестіруінің математикалық үміті және дисперсиясы:

және нің үлкен мәндерінде Фишер үлестіруі қалыпты үлестіруге ұқсайды. Фишер үлестіруі дисперсиялық және регрессиялық талдауда статистикалық болжамдарды тексеруге пайдаланылады.