Относительная погрешность измерения - отношение абсолютной погрешности измерения к истинному значению измеряемой величины:

. (2)

Относительная погрешность – безразмерная величина. Часто относительную погрешность выражают в процентах, принимая за 100 % истинное значение измеряемой величины.

Относительная погрешность измерений характеризует качество измерений: чем она меньше, тем качество выше. Для оценки качества измерений в метрологии пользуются поняти­ем точность измерений. Точность измерений (см. ф. (3)) – это качество измерений, отражающее близость их результатов к истинному значению измеряемой величины. Количест­венно точность может быть выражена обратной величиной модуля отно­сительной погрешности. Если, например, относительная погрешность измерений равна 0,1%= 0,001, то точность равна 1000.

, (3)

Приведенная погрешность измерения - это отношение абсолютной

погрешности к нормирующему значению измеряемой величины:

(4)

где X_N – нормирующее значение измеряемой величины.

Нормирующее значение - это установленное значение ширины диапазона или определенное значение, к которому относится выражение значения характеристики.

Нормирующее значение ХN принимается равным:

1) - конечному значению диапазона измерений - для приборов с односторонней шкалой;

2) - сумме конечных значений диапазона измерений - для приборов с двухсторонней шкалой;

3) - разности конечного и начального значений диапазона - для приборов с безнулевой шкалой.

При логарифмическом, гиперболическом и степенном характере шкалы прибора приведенную погрешность выражают в процентах от длины шкалы.

Класс точности – это максимально допустимая приведенная погрешность (в процентах) при нормальных условиях эксплуатации.

Погрешность в каждом отдельном измерении может быть и меньше максимальной. Поэтому класс точности не может служить непосредственным показателем точности прибора, он лишь определяет предельное возможное значение приведенной погрешности. ГОСТом установлены стандартные классы точности: 0,005, 0,002, 0,05, 0,1, 0,25, 0,5, 1,0, 1,5, 2,5, 4,0.

Класс точности, как правило, указывается непосредственно на лицевой панели прибора. Расшифровка обозначения класса точности в виде рисских цифр или букв раскрывается в нормативно-технической информации. Обозначение в виде арабских цифр непосредственно указывает класс точности.

Отметка снизу у обозначения класса точности, говорит о том, что у приборов данного типа имеющих существенно неравномерную шкалу погрешность не превосходит величину указанную в процентах, относительно 100 % шкалы или диапазона измерения.

Заключение класса точности в окружность говорит о том, что проценты вычисляются непосредственно от значения, указываемого указателем.

Иногда значение класса точности дается в виде дроби, в этом случае величина не может отличаться от значения x показываемого указателем более чем на величину 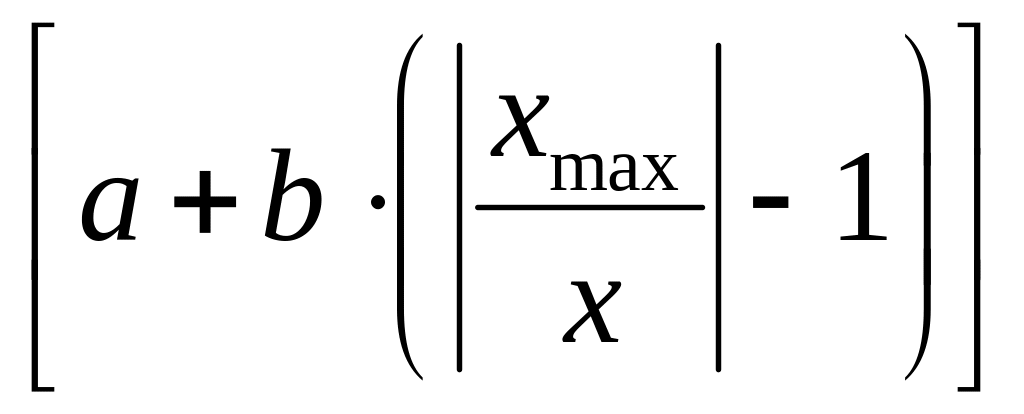, где a и b – числитель и знаменатель дроби.

Лекция № 4. Основные характеристики средств измерения.

Характеристики свойств средств измерений, оказывающих влияние на результаты измерений и их точность, называются метрологическими характеристиками средств измерений.

Их можно разбить на группы:

1. Характеристики, предназначенные для определения показаний средств измерений.

К ним относятся: функция преобразования; значения однозначной или многозначной меры; цена деления шкалы прибора; вид выходного кода, число разрядов кода, цена единицы наименьшего разряда кода для цифровых приборов.

2. Характеристики качества показаний - точности и правильности.

Точность показания определяется его средним квадратическим отклоне­нием или его аналогом. Правильность обеспечивается внесением поправ­ки, устанавливаемой при метрологической аттестации средства измере­ний.

3. Характеристики чувствительности средств измерений к влияющим величинам.

К ним относятся функции влияния и учет изменений метроло­гических характеристик средств измерений, вызванных изменениями влияющих величин в установленных пределах.

4. Динамические характеристики средств измерений, учитывающие их быстродействие (инерционность).

5. Характеристики взаимодействия с объектами или устройствами на входе и выходе средств измерений. Примерами характеристик этой группы являются входной и выходной импедансы линейного измерительного пре­образователя.

6. Неинформативные параметры выходного сигнала, обеспечивающие нормальную работу устройств, подключенных к средству измерений.

Отдельные виды средств измерений обладают своими специфи­ческими свойствами (параметрами). Вместе с тем они характеризуют­ся некоторыми общими свойствами, которые позволяют оценивать от­дельные средства измерений, а также сопоставлять их между собой.

7. Характеристики надежности и безотказности измерительного прибора.

Типовые метрологические характеристики первой группы нормируют как номинальные характеристики средств измерений данного типа. Номинальную функцию преобразования измерительного преобразователя представляют в виде формулы, таблицы, графика. Номинальные значения однозначной или многозначной меры представляют именованными числа­ми.

Дня конкретных экземпляров средств измерений нормируются преде­лы (граничные характеристики), в которых должна находиться индиви­дуальная метрологическая характеристика первой группы при предусмот­ренных условиях применения средства измерений.

Нормальные и рабочие условия применения средств измерений уста­навливаются в нормативно-технических документах на средства измере­ний. Нормальными считаются условия, при которых зависимостью метро­логических характеристик от изменения значений влияющих величин можно пренебречь. Так, для многих типов средств измерений нормальны­ми условиями являются: температура — (293 ± 5) К, относительная влаж­ность (65 ± 15) %, напряжение в сети питания 220 В ± 10 %. Рабочие условия отличаются от нормальных более широким диапазоном измене­ния значений влияющих величин,

При нормировании метрологических характеристик второй группы исходят из того, что правильность показаний средств измерений обеспечивается поправкой, точное значение которой для каждого конкретного эк­земпляра средств измерений неизвестно. Поэтому устанавливают пределы в которых должна находиться поправка у всех средств измерений данного типа.

Нормированные метрологические характеристики второй группы представляются либо одним числом, либо функцией (формулой, таблицей, графиком) информативного параметра входного или выходного сигна­ла.

Нормирование метрологических характеристик второй группы может производиться как для нормальных, так и для рабочих условий. В отли­чие от этого метрологические характеристики третьей группы нормируют­ся только для рабочих условий измерений. В рабочих условиях изменение значений влияющих величин начинает сказываться на точности и правиль­ности показаний. Это учитывается функциями влияния.

Учет всех нормируемых метрологических характеристик средств измерений — сложная и трудоемкая процедура, оправданная только при измерениях очень высокой точности, характерных для метрологической практики. В обиходе и на производстве, как правило, такая точность не нужна. Поэтому для средств измерений, используемых в повседневной практике, принято деление по точности на классы точности (см. предыдущую лекцию).

Одним из основных свойств измерительного прибора является его погрешность измерения, которая рассматривалась в предыдущей лекции.

С погрешностью тесно связана вариация показаний – наибольшая разность показаний измерительного средства при одном и том же значении измеряемой величины и неизменных внешних условиях, определённая при подходе к измеряемой величине сверху и снизу.

Градуировочной характеристикой измерительного преобразователя называется зависимость результата измерений от истинного значения измеряемой величины в установившемся режиме при постоянных значениях возмущений. Понятие градуировочной характеристики аналогично понятию статической характеристики элемента системы автоматики, например, первичного преобразователя или датчика, только вместо входного сигнала используется истинное значение измеряемой величины, а вместо выходного – результат измерения согласно отсчетному устройству измерительного прибора.

Градуировочные характеристики обычно изображаются в виде кривой или семейства кривых (для различных значений возмущений).

Чувствительностью (статическим коэффициентом передачи) измерительного прибора называют отношение приращения результата измерения к вызвавшему его приращению измеряемой величины на линейном участке градуировочной характеристики (см рис. 2)

. (5)

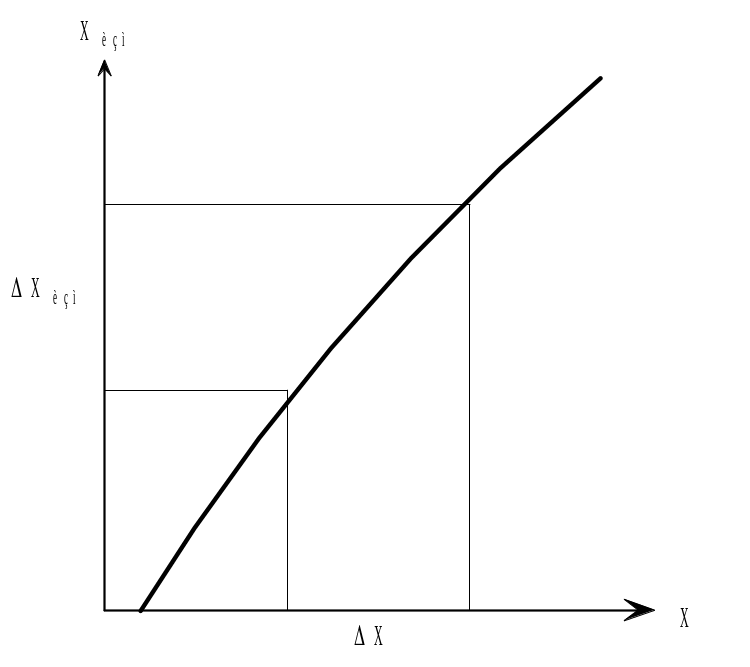
Рис. 2 Определение чувствительности средства измерения по градуировочной характеристике

Единицей измерения чувствительности является отношение размерности результата измерения к размерности истинного значения измеряемой величины, например для первичного преобразователя (датчика) давления с токовым выходом чувствительность будет измеряться в мА/Па.

Понятие чувствительности, как видно из определения, аналогично понятиям коэффициента усиления усилителя или статическому коэффициенту передачи. Динамической чувствительностью называют производную результата измерения по истинному значению измеряемой величины.

.

В идеальном случае, когда градировочная характеристика имеет вид прямолинейной зависимости идущей из точки (0;0), чувствительность будет определяться отношением результата измерений к измеряемой величине.

Порог чувствительности – наименьшее значение измеряемой величины, вызвавшее изменение показаний измерительного средства, обнаруживаемое наблюдателем.

Для цифровых приборов порог чувствительности определяется единицей младшего разряда. Для аналоговых приборов минимальным значением измеряемой величины, обнаруживаемым наблюдателем является значение, соответствующее первой отметке шкалы прибора.

Диапазон измерения - это область значений между нижним и верхним пределами измерений. Нижний и верхний пределы измерений – это min и max значения величины, которые могут быть измерены данным средством измерения с заданной погрешностью.

Динамический диапазон – отношений максимальной измеренной величины к значению минимальной измеренной величины (безразмерная величина).

.

Динамические характеристики характеризуют поведение объекта во времени. При этом выделяют 2 группы характеристик:

- полные динамические характеристики;

- частные динамические характеристик.

Полная динамическая характеристика средств измерения даёт возможность при любом заданном изменении во времени входной величины рассчитать изменение во времени выходной величины, т.е. тем самым позволяет определить погрешность измерения. Примером такой характеристики является дифференциальное уравнение, описывающее данный объект или передаточная функция преобразования (для линейных объектов).

Частная динамическая характеристика представляет собой один из параметров полной динамической характеристики: частотная динамическая характеристика, характеристика быстродействия (время преобразования), полоса пропускания частот.

Под надёжностью средств измерения понимается их способность сохранять нормированные метрологические характеристики в определённых условиях эксплуатации.

Выход хотя бы одного из метрологических параметров за пределы заданного понимается как отказ метрологического средства.

Параметры надёжности (рассматриваются в теории надежности):

1. Время наработки на отказ

2. Вероятность безотказной работы

3. Частота отказов.

Метод измерения – это совокупность приёмов и средств, используемых в измерительном процессе.

Процессы измерения отличаются методами организации сравнения измеряемой величины с мерой (приводимая далее классификация – классификация по признаку способа сравнения измеряемой величины с мерой).

В соответствии с ГОСТом все методы измерения делятся на две группы:

1. Методы прямого преобразования

2. Методы уравновешивания

Методы уравновешивания делятся на следующие группы:

1. Метод противопоставления

2. Дифференциальный метод

3. Нулевой метод

4. Метод замещения

5. Метод совпадений

Метод прямого преобразования

Этот метод характеризуется тем, что все преобразования информации осуществляются только в одном прямом направлении: от измеряемой величины Х через одну цепь измерительных преобразователей к выходной величине У.

Рис. 3

Характеристики метода.

Результирующая чувствительность всего канала измерения характеризуется произведением чувствительности всех включённых в цепь преобразователей, а результирующая погрешность в равной степени зависит от погрешностей каждого измерительного преобразователя, включённого в цепь. Любые изменения коэффициента передачи преобразователей в цепи измерения вызывают дополнительную погрешность.

Для устройств прямого преобразователя характерно отсутствие меры в явном виде, что является их главным недостатком. Процесс сравнения с мерой осуществляется косвенно, путём предварительной градуировки измерительного средства.

Измерительное средство прямого преобразования простое по конструкции и недорогое.

Методы уравновешивания

М етоды уравновешивания характеризуются тем, что измеряемая величина сравнивается с величиной воспроизводимой меры, для формирования которой используется специальная цепь обратного преобразования.

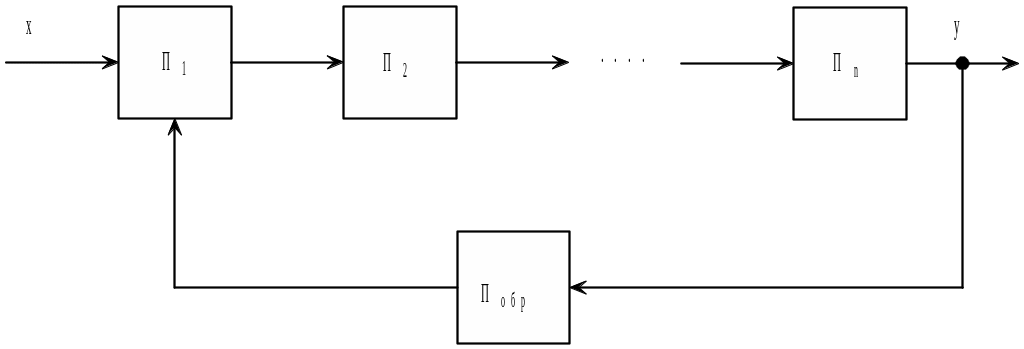
Рис. 5

Измерительная цепь характеризуется наличием двух цепей преобразователей. Первая – цепь прямого преобразования которая служит для преобразования измеряемой величины x в значение числовой оценки y. Вторая – цепь обратного преобразования служит для преобразования числовой оценки в значение физической величины Xk однородной измеряемой величине X, П_обр служит для формирования величины воспроизводимой меры.

Метод противопоставлений использует различные значения меры. Если имеется измеряемая величина x, то на измерительный прибор действуют одновременно две величины (измеряемая и величина из набора меры).

Дифференциальный метод основан на действии величины разности измеряемой величины и величины однозначной меры на измерительный прибор.

В нулевом методе измерения результат сравнения измеряемой величины доводят до нулевого значения, путем выбора соответствующего значения меры.

В методе замещения неизвестную величину поочерёдно замещают величиной воспроизводимой меры.

В методе совпадений разность между измеряемой величиной и величиной воспроизводимой меры определяют, используя совпадения отметок шкал или периодических сигналов.