
- •1.Об’єкт, предмет і методи статистики. Основні категорії статистики.
- •2.Поняття статистичного спостереження. Форми організації статистичного спостереження.
- •3.Види статистичного спостереження (за повнотою охоплення одиниць сукупності та часом реєстрації даних).
- •1.За часом реєстрації даних:
- •2.За повнотою охоплення статистичної сукупності:
- •3.За способом обліку даних.
- •4.Програмно-методологічні та організаційні питання статистичного спостереження.
- •5.Помилки спостереження та способи їх контролю.
- •6.Сутність статистичного зведення. Класифікація статистичних зведень (за складністю побудови, способом організації роботи, ступенем автоматизації обробки даних).
- •7.Поняття статистичного групування. Класифікація статистичних групувань (залежно від поставлених завдань, кількості групувальних ознак, кількості етапів проведення).
- •8.Ряди розподілу. Класифікація рядів розподілу. Зображення рядів розподілу.
- •9.Статистичні таблиці. Макет таблиці. Підмет і присудок статистичних таблиць. Статистичний графік.
- •10.Класифікація статистичних таблиць. Основні правила побудови статистичних таблиць.
- •11.Поняття та види абсолютних величин. Одиниці вимірювання абсолютних величин.
- •12.Поняття відносної величини. Форми та класифікація відносних величин.
- •13.Характеристика відносних показників динаміки, структури і координації.
- •14.Характеристика відносних показників планового завдання, виконання плану та порівняння.
- •15.Характеристика відносних показників інтенсивності та диференціації.
- •16.Суть і призначення середніх величин в статистиці. Класифікація середніх величин. Середня арифметична величина та її властивості.
- •17.Суть і призначення середніх величин в статистиці. Середня гармонічна та середня квадратична величина.
- •18.Суть і призначення середніх величин в статистиці. Середня геометрична, середня хронологічна та середня прогресивна величини.
- •19.Структурна середня: мода для дискретного та інтервального ряду розподілу. Графічний спосіб її визначення.
- •20.Структурна середня: медіана для дискретного та інтервального ряду розподілу. Графічний спосіб її визначення.
- •21.Поняття варіації кількісної ознаки. Абсолютні показники варіації та їх економічний зміст.
- •22.Поняття варіації кількісної ознаки. Відносні показники варіації та їх економічний зміст.
- •23.Види дисперсій та правило їх додавання. Емпіричний коефіцієнт детермінації та кореляційне відношення.
- •24.Основні показники форми розподілу. Асиметрія.
- •25.Основні показники форми розподілу. Ексцес.
- •26.Поняття вибіркового спостереження та види його переваги над іншими формами спостереження.
- •27.Основні завдання вибіркового спостереження. Помилки спостереження.
- •28.Методи формування вибірки (проста випадкова, механічна, типова, серійна, комбінована, багатофазова).
- •29.Середня (стандартна) помилка простої випадкової та механічної вибірки.
- •30.Середня (стандартна) помилка типової вибірки.
- •31.Середня (стандартна) помилка серійної вибірки.
- •32.Гранична помилка вибірки. Ймовірність появи помилки вибірки. Довірчі інтервали для генеральних характеристик вибірки.
- •33.Визначення необхідного об’єму вибірки.
- •34.Мала вибірка та її особливості.
- •35.Поширення результатів вибіркового спостереження на вибіркову сукупність.
- •36.Поняття та класифікація рядів динаміки.
- •37.Основні показники ряду динаміки. Показники динаміки рівнів.
- •38.Основні показники ряду динаміки. Середні показники динамічного ряду.
- •39.Методи виявлення основної тенденції (тренду) в рядах динаміки. Метод укрупнення інтервалів. Метод ковзної (плинної) середньої.
- •40.Методи виявлення основної тенденції (тренду) в рядах динаміки. Метод аналітичного вирівнювання.
- •41.Вимірювання коливань в рядах динаміки.
- •42.Виявлення та вимірювання сезонних коливань в рядах динаміки.
- •43.Автокореляція в рядах динаміки. Автокореляція між рівнями ряду.
- •44.Автокореляція в рядах динаміки. Автокореляція між залишковими величинами.
- •45.Кореляція рядів динаміки.
- •46.Визначення та класифікація індексів.
- •47.Індивідуальні індекси.
- •48.Загальні (зведені) індекси. Агрегатні індекси.
- •49.Загальні (зведені) індекси. Середні з індивідуальних (середньозважені) індекси.
- •50.Загальні (середні) індекси. Індекси середніх величин.
- •Метод паралельного порівняння рядів значень результативної та факторної ознак.
- •Графічний метод.
- •Метод аналітичних групувань і кореляційних таблиць.
- •58. Побудова рівняння парної регресії і перевірка його адекватності.
- •60 . Множинний кореляційно-регресивний аналіз.
Графічний метод.
Виявлення кореляційного зв’язку полягає у побудові на Декартові площині координат так званого кореляційного поля(сукупності точок (х,у), де х – значення факторної ознаки (абсциса), а у – значення результативної ознаки(ордината)). Кожній одиниці досліджуваної сукупності відповідає одна точка кореляційного поля. За характером розміщення точок роблять висновок про наявність чи відсутність зв’язку. А також про його напрям.
Якщо точки сконцентровані навколо певної лінії, спрямованої напрямку зростання х та у, то маємо прямий зв'язок.
Якщо у напрямку зростання х і спадання у – обернений зв'язок.
Якщо точки розкидані хаотично, без будь-якої тенденції, то це свідчить про відсутність кореляційної залежності між змінними х та у.
Метод аналітичних групувань і кореляційних таблиць.
згідно з цим методом, дані статистичного спостереження групуються за факторною ознакою х і для кожної виділеної групи розраховується середнє значення результативної ознаки у, тобто для кожного хі обчислюється відповідне . Якщо існує зв’язок між х та у, то в зміні середнього значення результативної ознаки буде простежуватись певна закономірність.
Статистичні
групування, за допомого яких виявляються
взаємозв’язки між ознаками називаються
аналітичними.
Результати групування часто оформляють
у вигляд таблиці розподілу одиниць
сукупності за двома ознаками. Такі
таблиці називають таблицями взаємної
спряженості, які у випадку двох кількісних
ознак ще називають кореляційними.
Будується кореляційна таблиця за типом
«шахової дошки». У її клітинках на
перетині відповідних значень х
та у
записують число nij
наявність пар (xi,,
yj).
За групованими даними будують також
емпіричну лінію регресії, тобто лінію,
яка проходить через точки (xi,,
).
У випадку, коли значення факторної
ознаки задається інтервалами замість
xi,
беруть
 - середнє значення і-го інтервалу). На
основі лінії емпіричної регресії частіше
всього передбачають наявність лінійного
чи нелінійного (криволінійного) зв’язку.
- середнє значення і-го інтервалу). На
основі лінії емпіричної регресії частіше
всього передбачають наявність лінійного
чи нелінійного (криволінійного) зв’язку.
52. У таких випадках для вивчення зв’язків між двома якісними ознаками будують так звані таблиці комбінаційного розподілу одиниць сукупності (респондентів) за двома досліджуваними ознаками – так звані таблиці взаємної спряженості.
Таблиці
взаємної спряженості можуть мати різну
розмірність. Найпростішою з таких
таблиць є таблиця «чотирьох полів». В
ній за кожною ознакою виділяється лише
дві групи спостережень, частіше всього
за альтернативним принципом («так» -
«ні», «добре» - «погано» і т.д.). Висновок
про наявність чи відсутність зв’язку
потрібно підсилити певним статистичним
критерієм, наприклад, критерієм
Пірсона
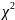 .
.
Він формалізується і з формул:
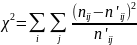 або
або
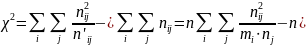 .
.
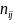 –
емпіричні
частоти
–
емпіричні
частоти
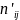 – теоретичні
частоти
– теоретичні
частоти
53. Для вимірювання тісноти зв’язку між кількісними показниками можуть використовувати лінійний коефіцієнт кореляції, емпіричне і теоретичне кореляційне відношення, коефіцієнт Фехнера, коефіцієнти кореляції рангів, коефіцієнт конкордації.
Лінійний коефіцієнт кореляції широко використовується для вимірювання тісноти лінійного зв’язку між двома кількісними ознаками х та у. якщо форма зв’язку ще не визначена, то даний коефіцієнт розраховується з метою відповісти на питання, чи можна залежність вважати лінійною.
Найбільш часто вживана формула для обчислення лінійного коефіцієнта кореляції має вигляд:
Емпіричне кореляційне відношення знаходять за формулою:
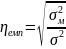
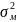 – між
групова дисперсія результативної
ознаки.
– між
групова дисперсія результативної
ознаки.
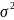 - загальна
дисперсія результативної ознаки.
- загальна
дисперсія результативної ознаки.
Емпіричне кореляційне відношення використовують, як правило, у тому випадку, коли статистичні дані згруповані у кореляційну таблицю.
Теоретичне кореляційне відношення обчислюється за формулою:

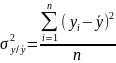
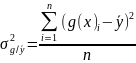
Зауважимо, що інколи кореляційне відношення називають індексом кореляції.
54. Коефіцієнт конкордації використовується для вимірювання тісноти зв’язку між ранжованими ознаками (факторними) у тому випадку, коли їх число більше двох.
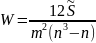
m – число ранжованих ознак;
n – кількість спостережень;
 -
сума квадратів відхилень сум m відповідних
рангів від середньої величини цих сум;
-
сума квадратів відхилень сум m відповідних
рангів від середньої величини цих сум;
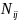 -
ранг і-го значення j-тої ознаки;
-
ранг і-го значення j-тої ознаки;
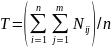 - середня
величина суми відповідних рангів.
- середня
величина суми відповідних рангів.
Якщо деякі ранги повторюються, тобто є зв’язаними, то коефіцієнт конкордації розраховується з урахуванням зв’язаних рангів для кожної ознаки:

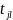 – число
однакових рангів групи
– число
однакових рангів групи
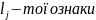 ;
;
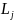 - число
всіх груп однакових рангів для j-тої
ознаки.
- число
всіх груп однакових рангів для j-тої
ознаки.
Даний коефіцієнт може набувати значень від 0 до 1. Значущість коефіцієнта конкордації при відсутності зв’язаних рангів оцінюється за допомогою критерію
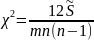
а при наявності зв’язаних рангів – за допомогою критерію
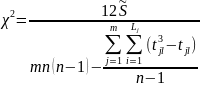
Коефіцієнт
Фехнера
– елементарна характеристика тісноти
зв’язку. Для його обчислення потрібно
визначити знаки («+» або «-») відхилень
індивідуальних значень кожної ознаки
від своєї середньої величини (тобто
знаки(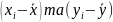 )
і підрахувати число їх збіжностей(
)
і підрахувати число їх збіжностей(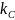 )
та незбіжностей(
)
та незбіжностей(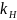 )
для кожного ряду.
)
для кожного ряду.
Формула для обчислення коефіцієнта Фехнера має вигляд:
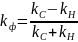
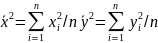
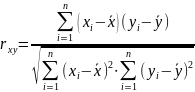
Очевидно,
що
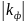 ≤1.
Наближення
до 1 свідчить про зростання тісноти
зв’язку між х
та у.
Однак при
=1
ще не можна стверджувати про наявність
функціонального зв’язку між ознаками.
≤1.
Наближення
до 1 свідчить про зростання тісноти
зв’язку між х
та у.
Однак при
=1
ще не можна стверджувати про наявність
функціонального зв’язку між ознаками.
Коефіцієнт Фехнера доцільно використовувати лише для встановлення факту наявності зв’язку при невеликому обсязі вихідної інформації.
55. Коефіцієнт кореляції рангів Спірмена і Кендела базуються на кореляції не самих значень корелюючих ознак, а їх рангів.
Ранг – це порядковий номер, який присвоюється окремо кожному індивідуальному значенню х та у у ранжованому ряді.
Значення обидвох ознак х та у ранжують(нумерують) у порядку зростання (1;n) або спадання (n;1).
Якщо зустрічаються декілька однакових значень ознаки, то кожному з них присвоюється ранг, рівний частці від ділення суми рангів (місць у ряді), виділених на ці значення на число рівних значень.
Висновок про зв'язок між х та у здійснюють на основі паралельного порівняння рангів обох ознак:
Якщо у кожної пари х та у ранги збігаються, то це характеризує максимально тісний прямий зв'язок:
Якщо у кожному ряді ранги зростають від 1 до n, а в другому – спадають від n до 1, то характеризує максимально тісний обернений зв'язок :
Коефіцієнт Спірмена обчислюється за формулою:
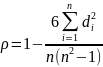
n-число всіх пар значень х та у (число рангів);
di = (Nxi-Nyi) – різниця рангів значень хі та уі.
Якщо
 маємо максимально тісни прямий зв'язок.
маємо максимально тісни прямий зв'язок.
Якщо
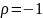 – максимально тісний обернений зв'язок.
– максимально тісний обернений зв'язок.
Якщо
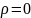 - зв'язок відсутній.
- зв'язок відсутній.
Коефіцієнт кореляції рангів Кендела
Для обчислення спочатку розміщують строго в порядку зростання ранги значень ознаки х, після чого паралельно записують відповідний до рагу Nx ранг Ny. Потім послідовність рангів ознаки у для кожного Ny послідовно визначають число Р наступних рангів, які є більшими від Ny , та число Q наступних рангів, які є меншими від Ny.
Якщо окремі значення ознак х та у не повторюються, то формула для обчислення коефіцієнта кореляції рангів Кендела має вигляд:

S=P-Q
Коефіцієнт
також змінюється в межах від (-1) до (+1),
при чому
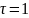 ,
коли ранги Ny
збігаються
з рангами Nx
і
,
коли ранги Ny
збігаються
з рангами Nx
і
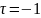 коли прямій послідовності рангів Nx
відповідає обернена послідовності
рангів Ny.
коли прямій послідовності рангів Nx
відповідає обернена послідовності
рангів Ny.
Якщо зустрічаються однакові значення ознаки х (чи) у, тобто ранги повторюються, то коефіцієнт кореляції рангів Кендела обчислюється за формулою:
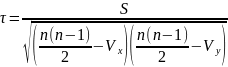
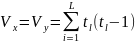
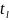 – число
однакових (тих, що повторюються) рангів
групи l
для х
та у;
– число
однакових (тих, що повторюються) рангів
групи l
для х
та у;
L – число всіх гру однакових рангів.
56. Для вимірювання тісноти зв’язку між двома якісним ознаками, розподіл одиниць сукупності яких задається таблицями взаємної спряженості, можуть бути використані такі показники, як коефіцієнти взаємної спряженості Пірсона і Чупрова.
Коефіцієнт асоціації формалізується так:
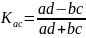 регресії.
регресії.
Числа a,b,c,d є частотами, у відповідних клітинках таблиці взаємної спряженості.
Коефіцієнт контингенції:
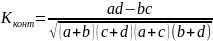
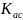 і
і
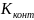 змінюються в межах від (-1) до (+1).
змінюються в межах від (-1) до (+1).
Коефіцієнь Пірсона та Чупрова
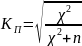
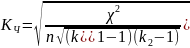
- число одиниць спостережень;
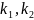 -
відповідне число рядків і стовпчиків
у таблиці.
-
відповідне число рядків і стовпчиків
у таблиці.
Обидва коефіцієнти змінюються в межах від 0 до 1.
