7Исследование влияния изменения шага дискретизации
7.1 Исследование влияния расчетного значения
Для исследования перепишем передаточные функции (3.2) и (3.3) так
(7.1)
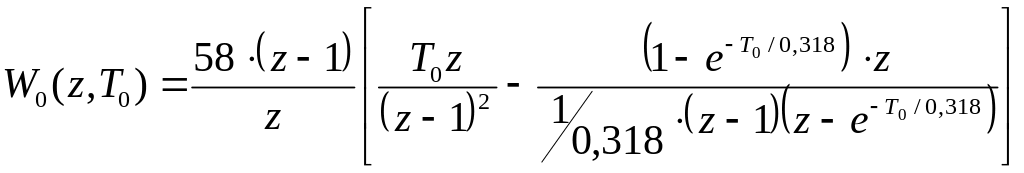(7.2)
Проделаем ту же работу, что в пункте 6, но меняя шаг дискретизации.
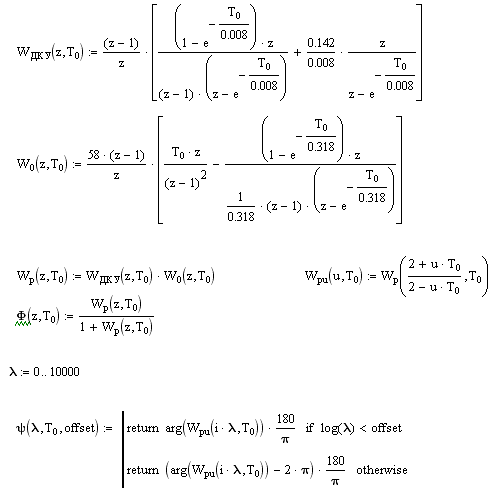
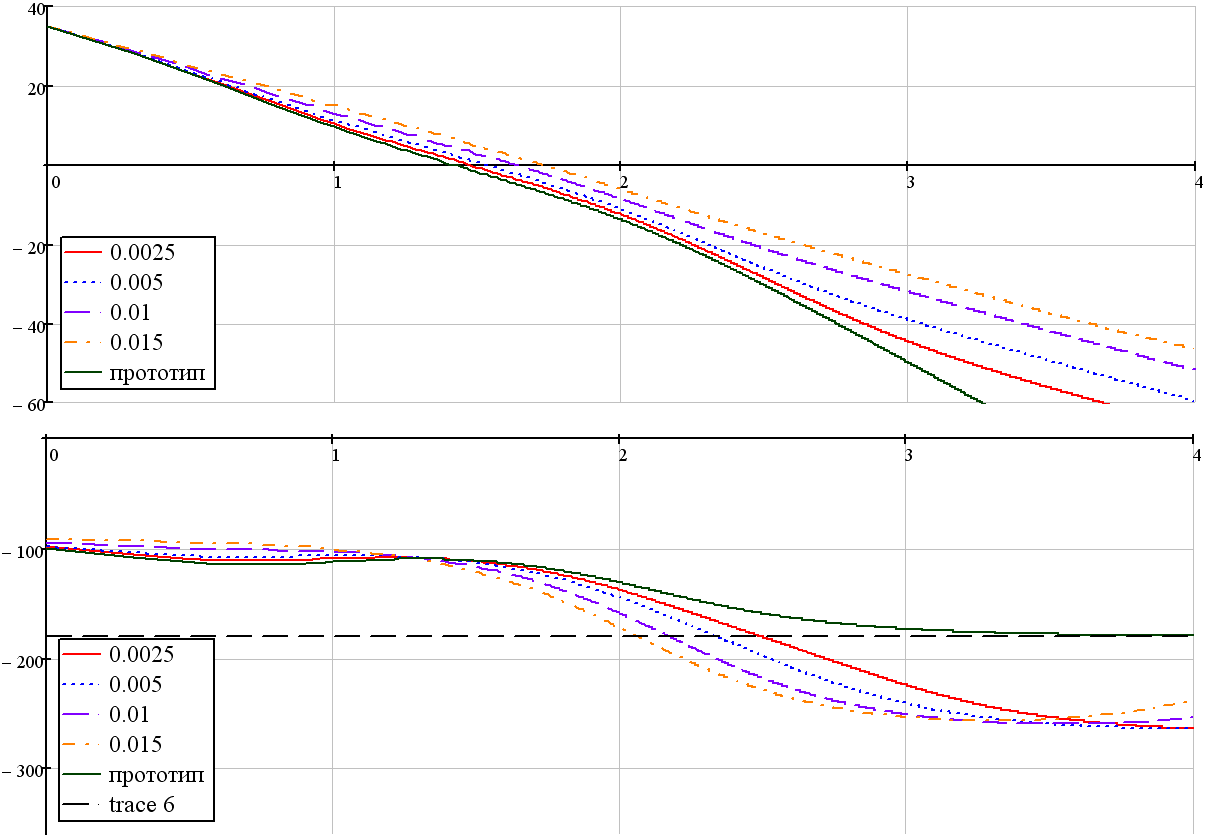
Рисунок 7.1 Влияние шага дискретизации на ПЧЛАХ и ПЧЛФХ
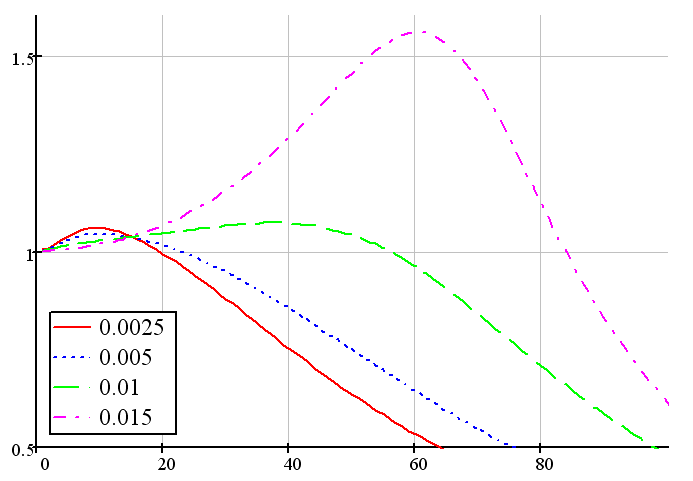
Рисунок 7.2 Влияние шага дискретизации на АЧХ
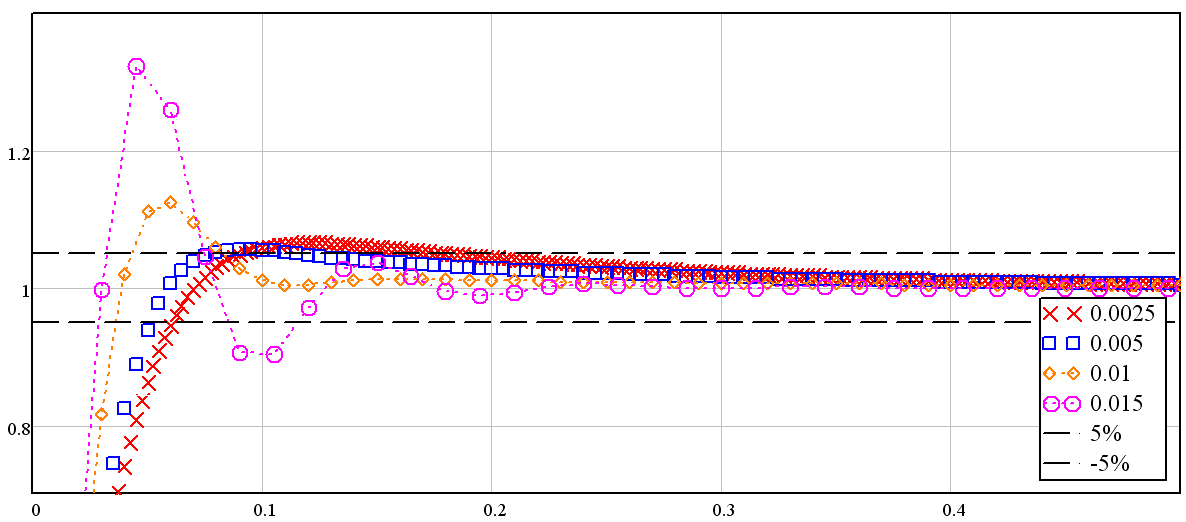
Рисунок 7.3 Влияние шага дискретизации на переходную характеристику
В таблицу 7.1 сведены все показатели в сравнении с системой эталоном.
Таблица 7.1 Сводная таблица
T0, с |
Lзап, дБ |
зап , градусы |
M
|
tp (5 %), c |
% |
0,0025 |
28,34 |
69 |
1,059 |
0,18 |
6,48 |
0,005 |
21,24 |
66 |
1,041 |
0,11 |
5,39 |
0,01 |
13,03 |
56 |
1,072 |
0,09 |
12,37 |
0,015 |
7,73 |
40 |
1,559 |
0,12 |
32,39 |
|
|
|
|
|
|
Система-прототип |
|||||
–– |
–– |
70 |
1,080 |
0,24 |
8,23 |
По таблице 7.1 видно, что с увеличением шага дискретизации увеличивается перерегулирование и уменьшается время регулирования. Чем меньше шаг дискретизации, тем точнее ДСАР повторяет систему-прототип. Нетрудно заметить, что ДСАР обладает лучшими прямыми показателями по сравнению с системой прототипом на малых шагах дискретизации. Увеличение шага дискретизации также негативно сказывается на запасах устойчивости. Дальнейшее увеличение шага дискретизации, в конечном счете, приведет систему к неустойчивому состоянию. Неустойчивое состояние наступает при шаге дискретизации большем или равном 0,025 с.
7.2 Исследование влияния фактического значения
В данном исследовании будем изменять шаг дискретизации только в УВХ 2 и фиксировать прямые показатели системы. За основу возьмем рисунок 1.1, а само исследование будем проводить в моделировщике VisSim.
На рисунке 7.4 показана общая диаграмма VisSim.
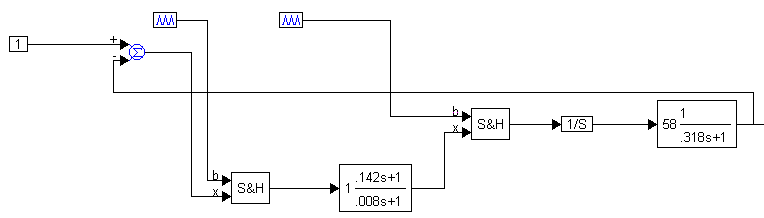
Рисунок 7.4 Общая схема исследования
На рисунке 7.5 показаны переходные характеристики системы для различных шагов дискретизации УВХ 2. В таблицу 7.2 сведены прямые показатели качества.
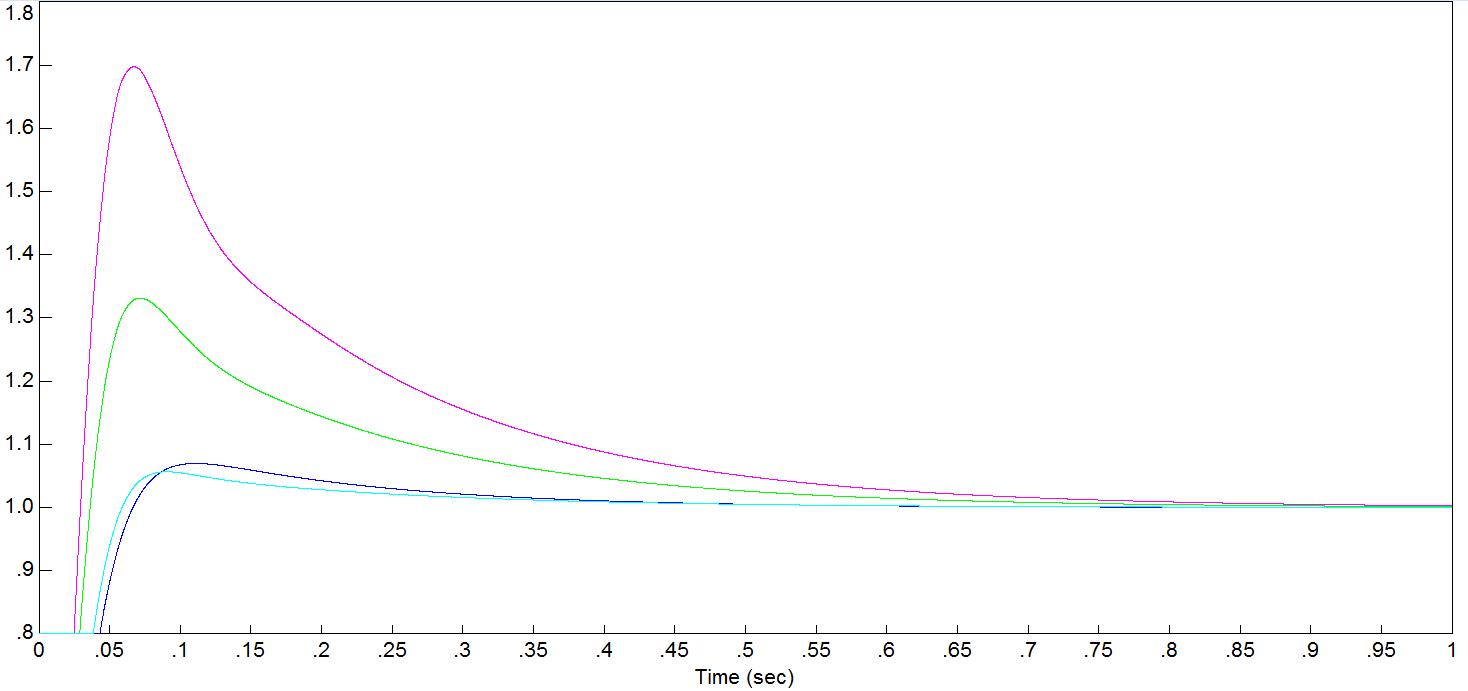
Рисунок 7.5 Переходные характеристики системы при различных шагах дискретизации звена УВХ 2
Таблица 7.2 Сводная таблица
T0, c |
tp (5%), с |
% |
0,0025 |
0,18 |
7 |
0,005 |
0,11 |
5,4 |
0,01 |
0,39 |
33 |
0,015 |
0,50 |
70 |
Из таблицы 7.2 можно очевидно, что изменение шага дискретизации в УВХ 2 негативно влияет на прямые показатели качества системы, как в сторону увеличения показателя, так и в сторону уменьшения.
8Исследование на возможность применения непрерывного прототипа
В качестве непрерывной модели исходной ДСАР будем рассматривать систему рисунка 8.1.
Рисунок 8.1 Непрерывная модель
Модель рисунка 8.1 определяется следующими передаточными функциями
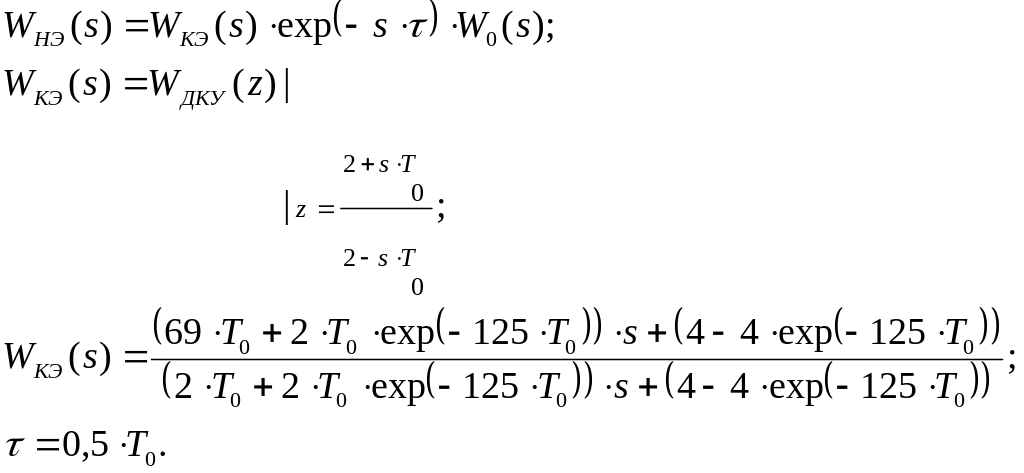
Будем изменять значения параметра T0 в большую сторону от рассчитанного ранее значения, и сравнивать переходную характеристику модели рисунка 8.1 с переходной характеристикой исходной ДСАР (рисунок 1.1).
Ниже в таблице 8.1 представлены передаточные функции элемента КЭ для шагов дискретизации 0,005; 0,01; 0,02.
Так для шага дискретизации 0,005 диаграмма VisSim будет выглядеть, как показано на рисунке 8.2. Для других шагов дискретизации диаграмма будет похожей с разницей на значение шага дискретизации и звена КЭ.
Таблица 8.1 Передаточная функция КЭ при различных шагах дискретизации
T0, c |
WКЭ(s) |
Рисунок |
0,005 |
|
8.3 |
0,01 |
|
8.4 |
0,02 |
|
8.5 |
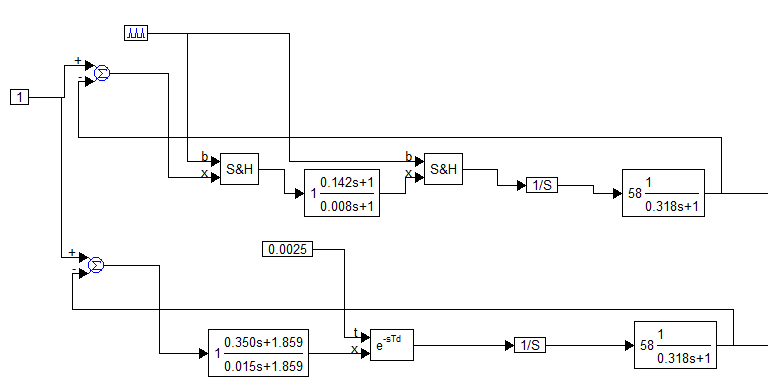
Рисунок 8.2 Диаграмма VisSim на примере шага дискретизации 0,005
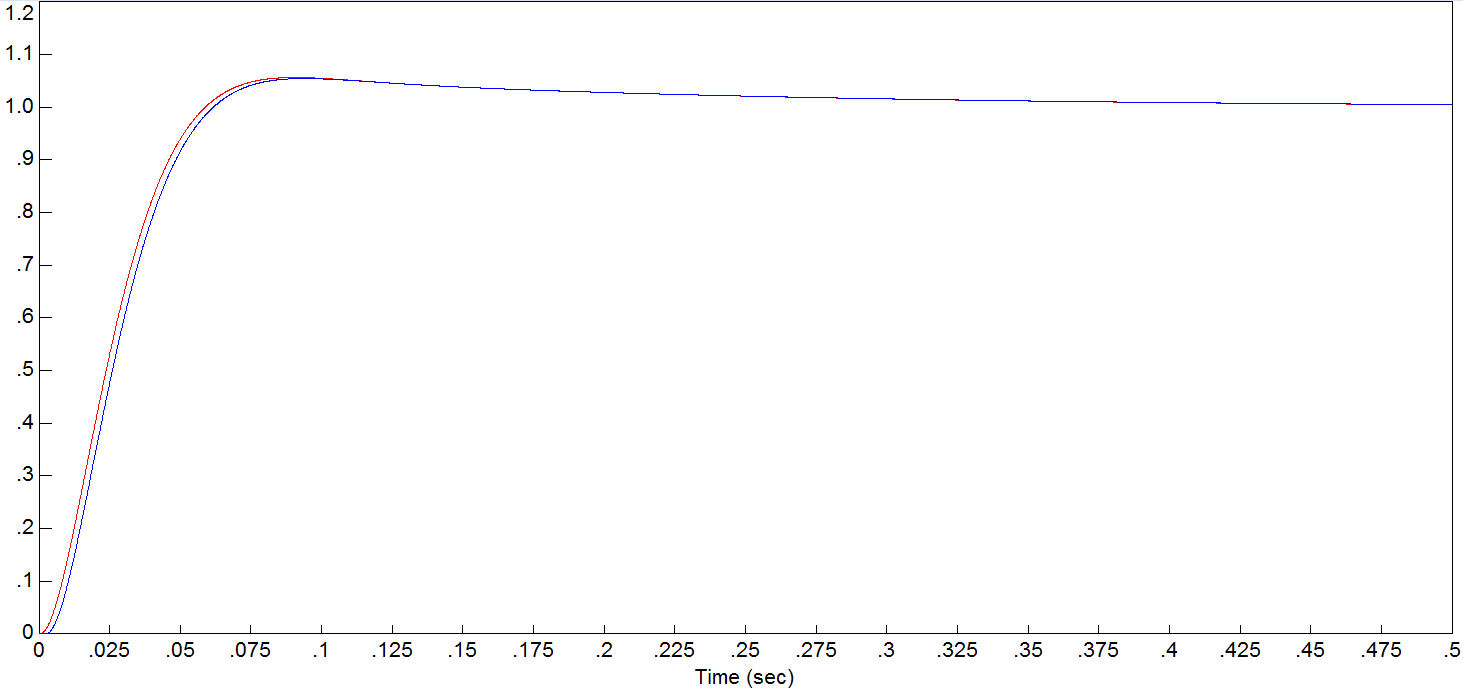
Рисунок 8.3 Графики при шаге дискретизации 0,005
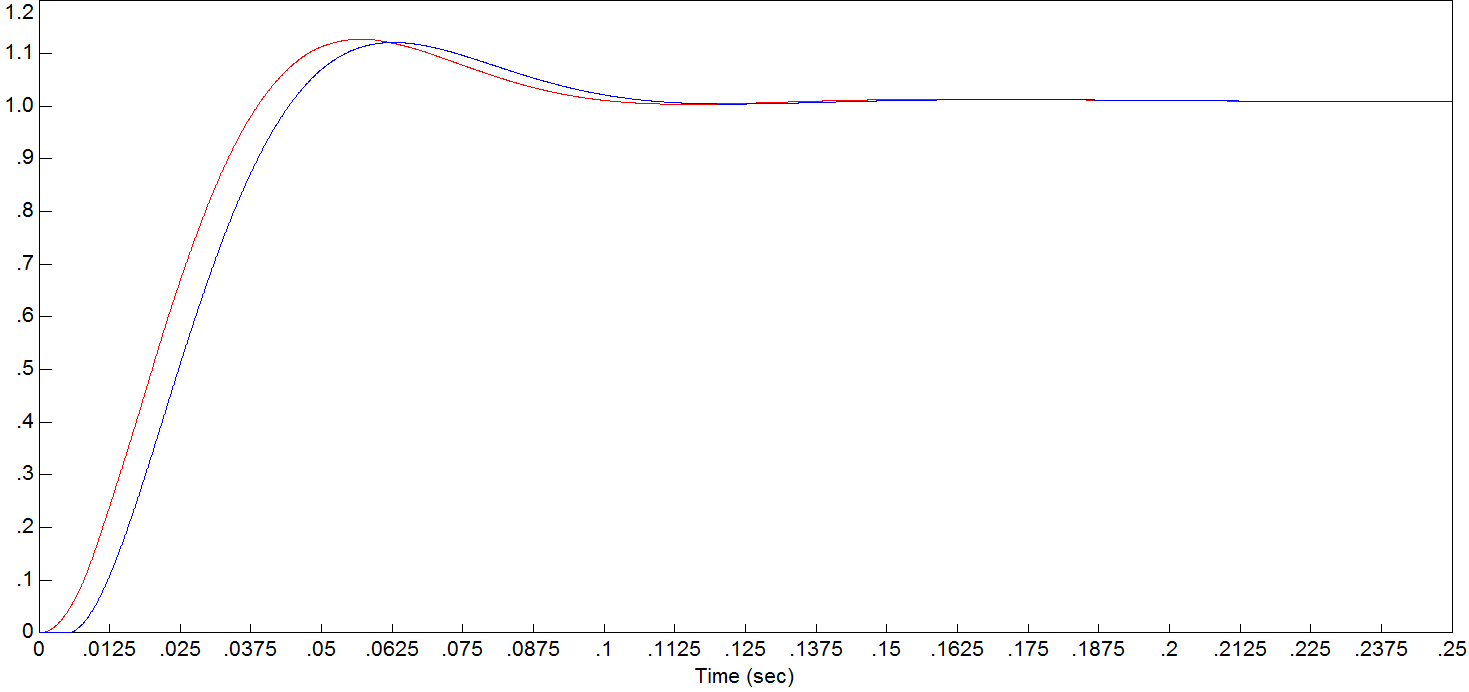
Рисунок 8.4 Графики при шаге дискретизации 0,01
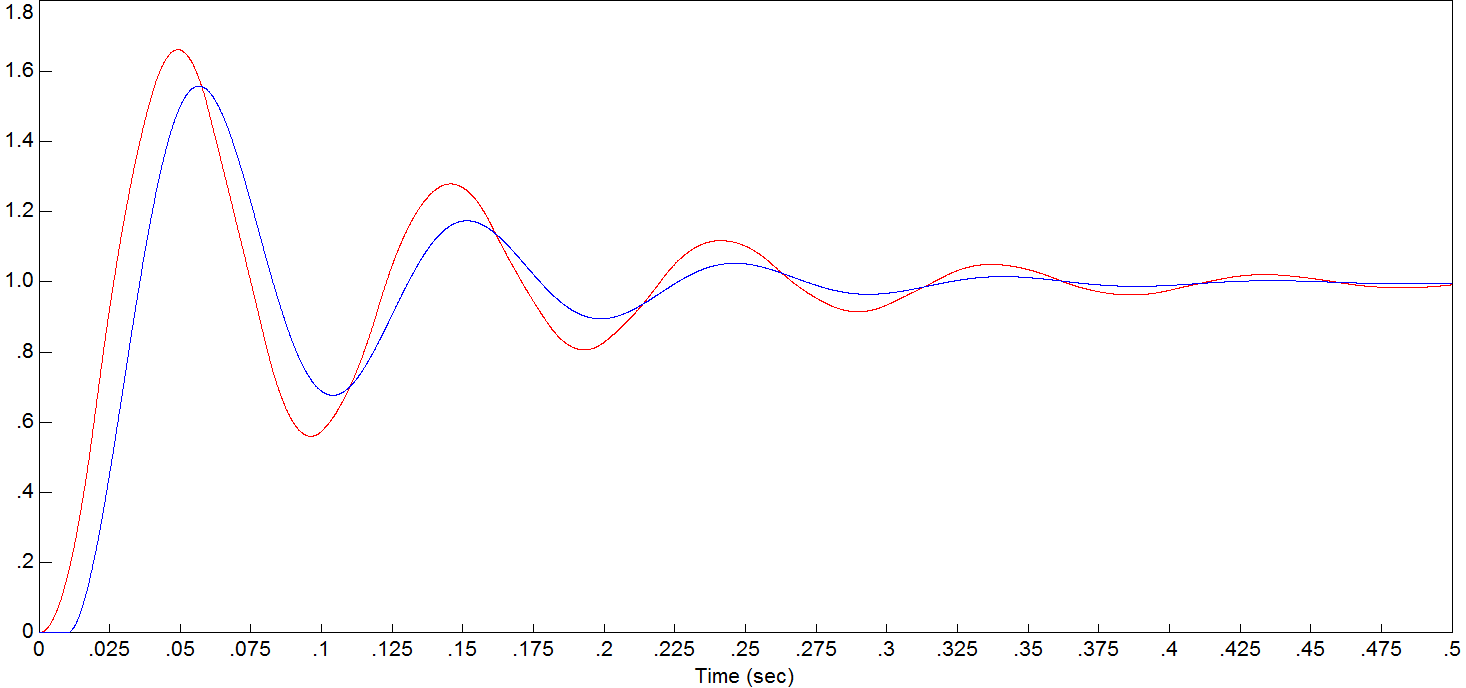
Рисунок 8.5 Графики при шаге дискретизации 0,02
Сравнивая перерегулирование в различных шагах дискретизации, можно сделать вывод, что непрерывный аналог достаточно точно описывает исходную ДСАР при шагах
.