5.2 Описание звена в уравнениях состояния

Описать данное звено можно в дискретных уравнениях состояния вида

Для заполнения матриц и векторов данной системы за основу необходимо снова взять за основу передаточную функцию (3.2).

Таким образом,

5.3 Построение частотных характеристик звена

Построим АЧХ звена, для чего в (3.2) сделаем подстановку

На рисунке 5.1 показана АЧХ звена

Рисунок 5.1 АЧХ ДКУ

Наконец, построим асимптотические ПЧЛАХ и ПЧЛФХ, для этого (3.4) перепишем так

Расчетное выражение для ПЧЛФХ будет следующим

На рисунке 5.2 изображены ЛПЧХ ДКУ.

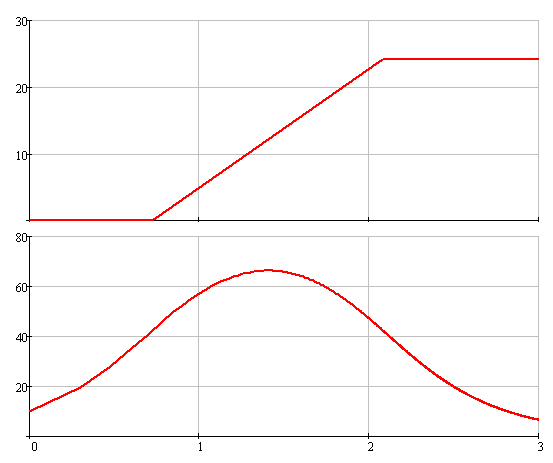
Рисунок 5.2 ЛПЧХ ДКУ

5.4 Построение переходной и весовой функции

Реакция звена на сигнал ₀[k] называется весовой функцией. Математическое описание данного сигнала имеет вид

0[k]=	1, k = 0;
	0, k  0.

График весовой функции можно получить по разностному уравнению 5.1, считая, что

На рисунке 5.3 показаны два способа нахождения весовой функции: через разностное уравнение 5.1 и через обратное z-преобразование произведения z-изображений передаточной функции (3.2) и ₀[k] функции.

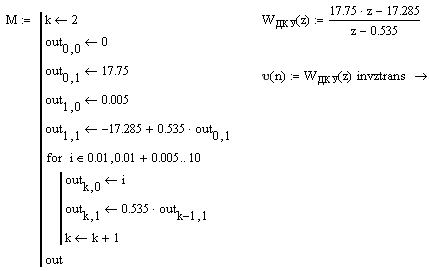
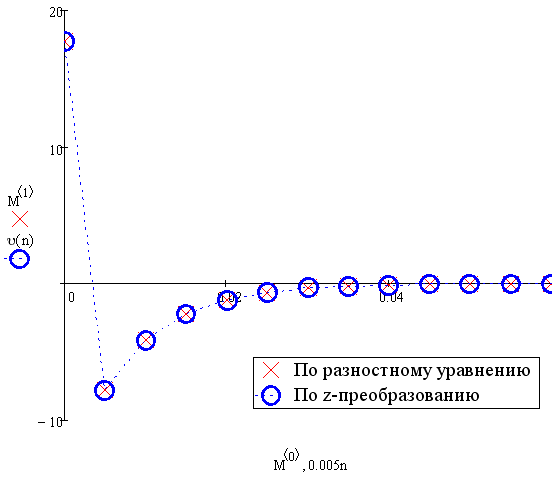
Рисунок 5.3 Весовая функция ДКУ

Переходной функцией называется реакция звена на сигнал 1[k], который принимает значение равное единице при любом k большим или равным нулю. Ее можно получить несколькими способами, но в пределах данного раздела мы воспользуемся следующими двумя: выполнив обратное z-преобразование следующего выражения

воспользовавшись связью переходной и весовой функций

где W[m] – весовая функция.

На рисунке 5.4 показана переходная функция ДКУ. Для построения вторым способом мы воспользовались данными из массива M, в который выше записывали значения весовой функции.

Рисунок 5.4 Переходная функция ДКУ

6Исследование замкнутой и разомкнутой системы

6.1 Исследование разомкнутой системы

Построим ЛПЧХ разомкнутой ДСАР и ЛЧХ системы-прототипа на одной плоскости и замерим необходимые показатели. Всю работу будем проводить в Mathcad.

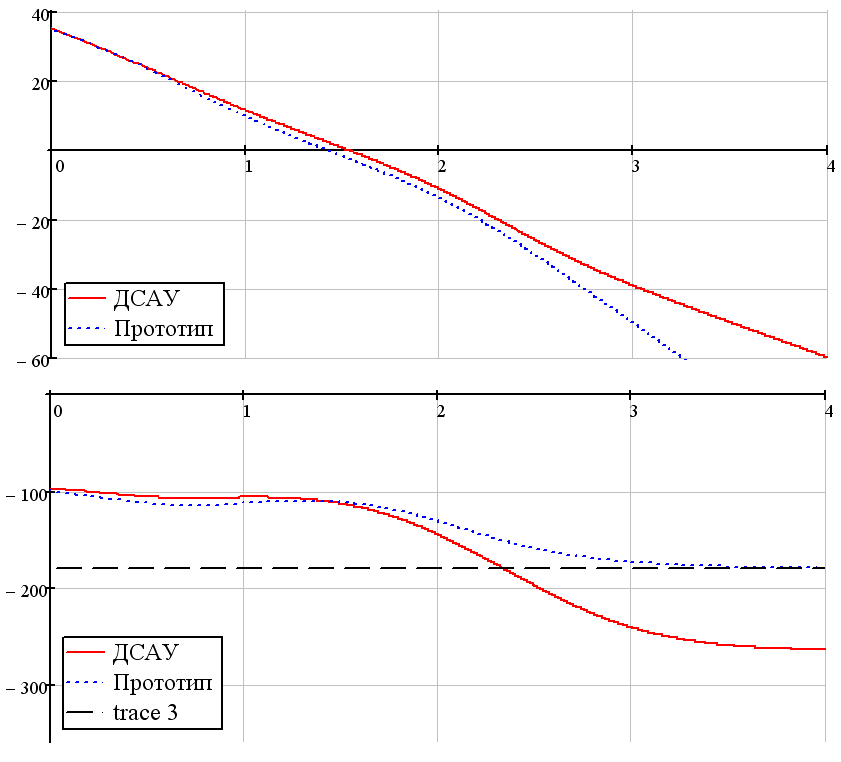
Рисунок 6.1 ЛПЧХ ДСАР и ЛЧХ прототипа

По характеристикам рисунка 6.1 сведем в таблицу 6.1 интересующие нас показатели

Таблица 6.1

	Критическая частота, дек	Частота среза, дек	Lзап, дБ	зап, градусы
ДСАР	2,34	1,53	21,24	66
Прототип		1,42	––	70

Определим критический коэффициент ДСАР, для чего воспользуемся следующим расчетным выражением

.

6.2 Исследование замкнутой системы

Сначала найдем показатели для системы-прототипа. Передаточная функция системы-прототипа с учетом (1.3) имеет вид

Определим нули и полюса системы прототипа, воспользовавшись Mathcad

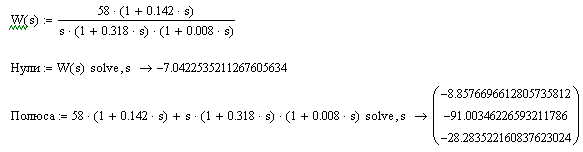
Откуда

В нахождении нулей и полюсов для ДСАР имеется отличие, которое заключается в использовании следующих соотношений [2, стр. 64]

Воспользуемся передаточной функцией (4.1) и рассчитаем нули и полюса

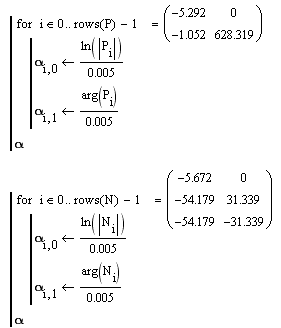
Откуда для ДСАР показатели следующие

Построим АЧХ для замкнутой ДСАР и замкнутой системы-прототипа (рисунок 6.2).

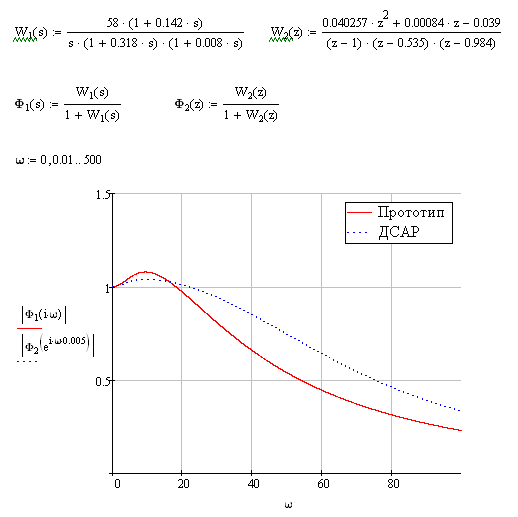
Рисунок 6.2 АЧХ системы-прототипа и ДСАР

По рисунку 6.2

Построим переходные характеристики для замкнутых систем, для чего воспользуемся возможностью обратного преобразования Лапласа и обратного z-преобразования (Рисунок 6.3).

Рисунок 6.3 Переходные характеристики

Для сравнения сведем все результаты в таблицу 6.2.

Таблица 6.2 Показатели качества ДСАР и системы-прототипа

Показатель	ДСАР	Система-прототип
	5,672	8,858
	0,578	0
M	1,041	1,080
tp, c (5 %)	0,11	0,24
 %	5,39	8,23

По сравнительной таблице 6.2 ДСАР обладает лучшими прямыми показателями и лучшим показателем колебательности, чем система-прототип, но худшими корневыми показателями.