31. Туннельный эффект.

В результате туннельного эффекта микрообъект может «пройти» сквозь потенциальный барьер.

Для описания туннельного эффекта используют понятие коэффициента про­зрачности D потенциального барьера, оп­ределяемого как отношение плотности по­тока прошедших частиц к плотности по­тока падающих. Можно показать, что

D=|A₃|²/|A₁|².

Для того чтобы найти отношение |А₃/А₁|², необходимо воспользоваться условиями непрерывности  и ' на границах барьера х=0 и х=l (рис. 298):

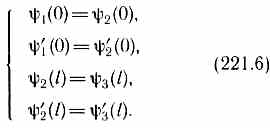
Эти четыре условия дают возможность выразить коэффициенты А₂, а₃, В₁ и В₂ через А₁. Совместное решение уравнений (221.6) для прямоугольного потенциаль­ного барьера дает (в предположении, что коэффициент прозрачности мал по сравне­нию с единицей)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барь­ера, Do — постоянный множитель, кото­рый можно приравнять единице. Из выражения (221.7) следует, что D сильно зависит от массы m частицы, шири­ны l барьера и от (U-E); чем шире барь­ер, тем меньше вероятность прохождения сквозь него частицы.

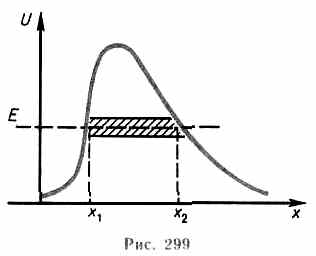
Туннельный эф­фект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может про­никнуть, можно пояснить соотношением неопределенностей. Неопределенность им­пульса p на отрезке x=l составляет p>h/l. Связанная с этим разбросом в значениях импульса кинетическая энер­гия (p)²/(2m) может оказаться достаточ­ной для того, чтобы полная энергия части­цы оказалась больше потенциальной.

32. Атом водорода

Потенциальная энергия взаимодейст­вия электрона с ядром, обладающим за­рядом 2е (для атома водорода Z=1),

U(r)=-Ze²/4₀r, (223.1)

где r — расстояние между электроном и ядром.

Состояние электрона в атоме водорода описывается волновой функцией , удов­летворяющей стационарному уравнению Шредингера (217.5), учитывающему значение (223.1):

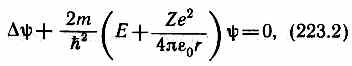
где т — масса электрона, Е — полная энергия электрона в атоме.

1. Энергия.

Самый нижний уро­вень Е₁, отвечающий минимальной воз­можной энергии,— основной, все осталь­ные (E_n>E₁ n=2, 3, ...) — возбужденные. При E<0 движение электрона является связанным — он находится внут­ри гиперболической «потенциальной ямы. По мере роста главного квантового числа n энергетиче­ские уровни располагаются теснее и при n= E_=0. При E>0 движение элек­трона является свободным; область непре­рывного спектра £>0 соответствует ионизованному атому. Энергия ионизации атома водорода равна E_i=-E₁= те⁴/ (8h²²₀)=13,55 эВ.

2. Квантовые числа. Главное квантовое число n определяет энергетические уровни электрона в атоме и может принимать любые целочисленные значения начиная с единицы: n=1,2,3, ....

момент импульса электрона квантуется, т. е. не может быть произволь­ным, а принимает дискретные значения, определяемые формулой L_e=h(l(l+1)), (223.4)

где l — орбитальное квантовое число, ко­торое при заданном n принимает значения

l=0, 1, ..., (n-1), (223.5) т. е. всего n значений, и определяет мо­мент импульса электрона в атоме.

Вектор L_e момента им­пульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция L_ez на направление z внешне­го магнитного поля принимает квантован­ные значения, кратные h

L_еz=hm_l, (223.6)

где m_l — магнитное квантовое число, кото­рое при заданном l может принимать зна­чения

m_l=0, ±1, ±2, ..., ±l, (223.7)

т. е. всего 2l+1 значений. Таким образом, магнитное квантовое число m_l определяет проекцию момента импульса электрона на заданное направление, причем вектор мо­мента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации.

Расщепление энергетических уровней в магнитном поле получило название эффекта Зеемана. Расщепление уровней энергии во внешнем электрическом поле назы­вается эффектом Штарка.

3. Спектр. В квантовой механике вводятся прави­ла отбора, ограничивающие число воз­можных переходов электронов в атоме, связанных с испусканием и поглощением света. Теоретически доказано и экспери­ментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие пере­ходы, для которых: 1) изменение орби­тального квантового числа l удовлетво­ряет условию

l=±1; (223.9)

2) изменение магнитного квантового чис­ла m_l удовлетворяет условию

m_l=0, ±1.

Переход электрона из основного со­стояния в возбужденное обусловлен увеличением энергии атома и может происхо­дить только при сообщении атому энергии извне, например за счет поглощения ато­мом фотона. Так как поглощающий атом находится обычно в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 1s np (n=2, 3, ...).

33. Процесс испускания фотона возбужденным атомом (возбужденной микросистемой) без каких-либо внешних воз­действий называется спонтанным (или самопроизвольным) излучением. Чем больше вероятность спонтанных переходов, тем меньше среднее время жизни атома в возбужденном состоянии. Так как спонтанные переходы взаимно не связаны, то спонтанное излучение некогерентно.

Если на атом, находящийся в возбуж­денном состоянии 2, действует внешнее излучение с частотой, удовлетворяющей усло­вию hv=E₂–E₁, то возникает вынужденный (индуцированный) переход в основное состояние 1 с излучением фотона той же энергии hv=E₂–E₁ (рис. 309, в). При подобном переходе происходит излучение атомом фотона, дополнительно к тому фотону, под действием которого произошел переход. Возникающее в результате таких переходов излучение называется вынужденным (индуцированным) излучением. Таким образом, в процесс вынужденного излучения вовлечены два фотона: первичный фотон, вызыва­ющий испускание излучения возбужденным атомом, и вторичный фотон, испущенный атомом. Существенно, что вторичные фотоны неотличимы от первичных, являясь точной их копией.

34. N_m - плотность атомов в

состоянии m ; N_n - плотность атомов в состоянии n .

Если заселенность возбужденного состояния больше, чем основного, т.е. n m N > N , в

среде будет происходить усиление света. Такое состояние называется состоянием с

инверсной заселенностью. Оно не является термодинамически равновесным. Согласно (11),

ему должна соответствовать отрицательная абсолютная температура. Инверсную

заселенность можно создать на ограниченный промежуток времени, возбуждая среду каким-

либо образом, т.е. сообщая ей энергию. В физике лазеров используют термин "накачка".

Явление усиления света в средах с инверсионной заселенностью уровней положено в основу

работы лазеров.

35. Ла́зер — опти́ческий ква́нтовый генера́тор — устройство, преобразующее энергию накачки (световую,электрическую, тепловую, химическую и др.) в энергию когерентного, монохроматического, поляризованного и узконаправленного потока излучения.

Физической основой работы лазера служит квантовомеханическое явление вынужденного (индуцированного) излучения. Излучение лазера может быть непрерывным, с постоянной мощностью, или импульсным, достигающим предельно больших пиковых мощностей. В некоторых схемах рабочий элемент лазера используется в качестве оптического усилителя для излучения от другого источника. Существует большое количество видов лазеров, использующих в качестве рабочей среды все агрегатные состояния вещества. Некоторые типы лазеров, например лазеры на растворах красителей или полихроматические твердотельные лазеры, могут генерировать целый набор частот (мод оптического резонатора) в широком спектральном диапазоне. Габариты лазеров разнятся от микроскопических для ряда полупроводниковых лазеров до размеров футбольного поля для некоторых лазеров на неодимовом стекле. Уникальные свойства излучения лазеров позволили использовать их в различных отраслях наукии техники, а также в быту, начиная с чтения и записи компакт-дисков и заканчивая исследованиями в области управляемого термоядерного синтеза.

36. Электрон в атоме движется вокруг ядра. В классической физике движению точки по окружности соответствует момент импульса L=mvr, где m – масса частицы, v – её скорость, r – радиус траектории. В квантовой механике эта формула неприменима, так как неопределенны одновременно радиус и скорость (см. "Соотношение неопределенностей"). Но сама величина момента импульса существует. Как его определить? Из квантово-механической теории атома водорода следует, что модуль момента импульса электрона может принимать следующие дискретныезначения:

(40)

где l – так называемое орбитальное квантовое число, l = 0, 1, 2, … n-1. Таким образом, момент импульса электрона, как и энергия, квантуется, т.е. принимает дискретные значения. Заметим, что при больших значениях квантового числа l (l >>1) уравнение (40) примет вид  . Это не что иное, как один из постулатов Н. Бора.

Из квантово-механической теории атома водорода следует еще один важный вывод: проекция момента импульса электрона на какое-либо заданное направление в пространстве z (например, на направление силовых линий магнитного или электрического поля) также квантуется по правилу:

(41)

где m = 0, ± 1, ± 2, …± l – так называемое магнитное квантовое число.

Электрон, движущийся вокруг ядра, представляет собой элементарный круговой электрический ток. Такому току соответствует магнитный момент p_m . Очевидно, что он пропорционален механическому моменту импульса L. Отношение магнитного момента p_m электрона к механическому моменту импульса L называется гиромагнитным отношением. Для электрона в атоме водорода

(42)

(знак минус показывает, что вектора магнитного и механического моментов направлены в противоположные стороны). Отсюда можно найти так называемый орбитальный магнитный моментэлектрона:

(43)

Эта величина,как видим, также квантуется.

В формуле (43) величина   является константой. Обозначим её _в и назовем магнетоном Бора. Магнетон Бора служит естественной единицей магнитного момента электрона, так как значения магнитного момента кратны величине _в :

37. Принцип тождественности одинаковых частиц гласит, что в замкнутой системе для одинаковых (то есть обладающих одинаковыми свойствами: массой, зарядом, спином и т. п.) частиц реализуются только такие квантовые состояния, которые не меняются при перестановке местами двух любых частиц.

38. Все частицы имеют либо целый, либо полуцелый спин. Частицы с полуцелым спином называются фермионами и подчиняются статистике Ферми, согласно которой данное состояние может занимать не более,чем один фермион. Волновая функция системы фермионов антисимметрична относительно перестановок переменных фермионов. Частицы с целым спином называются бозонами и подчиняются статистике Бозе, согласно которой данное состояние может занимать произвольное количество бозонов. Волновая функция системы бозонов симметрична относительно перестановок переменных бозонов. В дальнейшем мы неоднократно столкнемся с проявлениями принципов Ферми и Бозе в физике адронов.

39. в одном квантовом состоянии может находиться только одна частица. Такие частицы называются фермионами и подчиняются квантовой статистике Ферми-Дирака. Иной квантовой статистикой описываются частицы с нулевым и целым спином. Эти частицы не подчиняются принципу Паули и в одном состоянии их может бытьсколько угодно. Такие частицы называютсябозонами, квантовая статистика, которая описывает их распределение по энергиям, - статистикой Бозе-Эйнштейна.

Идеальный газ из бозонов — бозе-газ — описывается квантовой статистикой Бозе - Эйнштейна.* Распределение бозонов по энергиям вытекает из так называемого большого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов в данном квантовом состоянии может быть любым:

                                                   (235.1)

* Ш. Бозе (1894—1974) — индийский физик.

 

Это распределение называется распределением Бозе - Эйнштейна. Здесь N_i — сред­нее число бозонов в квантовом состоянии с энергией E_i, k —постоянная Больцмана, Т—термодинамическая температура,  —химический потенциал;  не зависит от энергии, а определяется только температурой и плотностью числа частиц. Химический потенциал находится обычно из условия, что сумма всех N_i равна полному числу частиц в системе. Здесь   0, так как иначе среднее число частиц в данном квантовом состоянии отрицательно, что не имеет физического смысла. Он определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия (энтропия, объем), фик­сированы.

Идеальный газ из фермионов — ферми-газ — описывается квантовой статистикой Ферми - Дирака.* Распределение фермионов по энергиям имеет вид

                                                   (235.2)

где N_i — среднее число фермионов в квантовом состоянии с энергией Е_i,  — химический потенциал. В отличие от (235.1)  может иметь положительное значение (это не приводит к отрицательным значениям чисел N_i). Это распределение называется распределением Ферми - Дирака.

40. самой важной с точки зрения теории электрической проводимости является валентная зона — размытый на подуровни внешний слой электронной оболочки атомов, который у большинства веществ не заполнен (исключение — инертные газы, но они кристаллизуются лишь при сверхнизких температурах). Поскольку внешний слой не насыщен электронами, в нем всегда имеются свободные подуровни, которые могут занять электроны из внешней оболочки соседних атомов. И электроны, действительно, проявляют удивительную подвижность, хаотично мигрируя от атома к атому в пределах валентной зоны, а в присутствии внешней разности электрических потенциалов они дружно «маршируют» в одном направлении, и мы наблюдаем электрический ток. Именно поэтому нижний слой, в котором имеются свободно перемещающиеся электроны, принято называть зоной проводимости — при этом это даже не обязательно самый верхний (валентный) орбитальный слой электронов в атоме.

41. В основе зонной теории лежат следующие главные приближения:^[1]

1. Твёрдое тело представляет собой идеально периодический кристалл.

2. Равновесные положения узлов кристаллической решётки фиксированы, то есть ядра атомов считаются неподвижными (адиабатическое приближение). Малые колебания атомов вокруг равновесных положений, которые могут быть описаны как фононы, вводятся впоследствии как возмущение электронного энергетического спектра.

3. Многоэлектронная задача сводится к одноэлектронной: воздействие на данный электрон всех остальных описывается некоторым усредненным периодическим полем.

42.  Зона проводимости - образована энергетическими уровнями, находясь на которых электрон является обобществленным, т.е. не связанным с отдельным атомом (зона свободных электронов). Если в зоне проводимости есть электроны, то при приложении электрического поля по веществу будет протекать ток.

            В металлах (I) валентная зона не полностью заполнена электронами. Электронам, находящимся на верхних энергетических уровнях, достаточно сообщить энергию ^-23 эВ, чтобы перевести их на более высокие уровни, сделать свободными. Энергия теплового движения (kТ) составляет при 1К величину порядка 10^-4 эВ, т.е. при  температурах имеются свободные электроны и такое твердое тело будет проводником, т.е. в металлах () валентная зона частично заполнена и является зоной проводимости. В металлах (II) зона проводимости перекрывается с валентной зоной. В этом случае образуется широкая «гибридная» зона, которую валентные электроны заполняют лишь частично. Выше занятых уровней расположены свободные уровни и такое твердое тело, как и в случае () будет проводником.

            Зонная теория твердых тел позволила объяснить, почему электропроводимость не возрастает с увеличением валентности металла, как это следует из кинетической теории. Al³⁺, следовательно, имеет 3 валентных электрона, т.е. проводимость по классической теории должна быть больше чем у Cu¹⁺ ( 1 валентный электрон ). С современной точки зрения электропроводность зависит не от числа валентных электронов, а от числа электронов, для которых в верхней зоне проводимости имеется достаточное число свободных  энергетических состояний.

            У двухвалентных металлов имеется некоторое число свободных энергетических уровней в зоне проводимости. Но число электронов, которые могут быть переведены внешним электрическим полем в свободные состояния меньше, чем у одновалентных металлов. Еще меньше таких электронов у трехвалентных металлов.

            У диэлектриков (III) валентная зона заполнена полностью, ширина запрещенной зоны велика (  3 эВ) тепловое движение не может перебросить электрон из валентной зоны в зону проводимости. Только при приложении очень сильных электрических полей возможен переход электрона в зону проводимости (пробой диэлектрика при пробивных напряжениях, зависящих от рода материала и его толщины).

            У полупроводников (IV) валентная зона заполнена полностью. Ширина запрещенной зоны невелика (   эВ). При температурах  200 – 300 С или внешних воздействиях (например, облучение светом - внутренний фотоэффект) электроны переходят из валентной зоны в зону проводимости и по полупроводниках протекает ток.

43. СОБСТВЕННАЯ ПРОВОДИМОСТЬ - проводимость полупроводника, обусловленная электронами, возбуждёнными из валентной зоны в зону проводимости и дырками, образовавшимися в валентной зоне. Концентрации n_i таких (зонных) электронов н дырок равны, и их можно выразить через эфф. плотности состояний в зоне проводимости (N_c)и в валентной зоне (N_v), ширину запрещённой зоны  и абс. темп-руТ: 

Т. к. проводимость  полупроводника пропорциональна концентрации свободных носителей заряда и их подвижности , то в пренебрежении слабыми степенными зависимостями N_c, N_vи  от темп-ры для собств. полупроводников можно получить соотношение: 

44,45. Примесной проводимостью полупроводников называется проводимость, обусловленная электронами, которые перешли в зону проводимости с донорных уровней Ed, расположенных вблизи Ec, и дырками, которые образовались в валентной зоне при переходе электронов на акцепторные уровни Ea, расположенные вблизи Ev (рис. 1а, 1б).

 

44.Примесный полупроводник n-типа

 

 

Рис. 1а

 

45.Примесный полупроводник p-типа

 

 

Рис. 1б

 

Обычно донорные и акцепторные уровни в запрещенной зоне полупроводника образуются при легировании, т.е. введением определенной примеси в собственный полупроводник. Таким образом можно сказать, что примесная проводимость обусловлена ионизацией атомов примеси в полупроводнике.

46. электронно-дырочный переход — область пространства на стыке двухполупроводников p- и n-типа, в которой происходит переход от одного типа проводимости к другому. p-n-Переход является основой для полупроводниковых диодов, триодов и других электронных элементов с нелинейной вольт-амперной характеристикой.

47. Атомное ядро состоит из элементарных частиц - протонов и нейтронов. Сейчас протонно-нейтронная модель ядра не вызывает сомнений. Рассматривалась также гипотеза о протонно-электронном строении ядра, но она не выдержала экспериментальной проверки. Так как атом нейтрален, то заряд ядра определяет и число электронов в атоме. От числа же электронов зависит их распределение по состояниям в атоме, от которого, в свою очередь, зависят химические свойства атома. Следовательно, заряд ядра определяет специфику данного химического элемента, т.е. определяет число электронов в атоме, конфигурацию их электронных оболочек, величину и характер внутриатомного электрического поля.

48. Ядро любого атома имеет сложную структуру и состоит из час­тиц, называемых нуклонами.  Известно два типа нуклонов -протоны и нейтроны. Протоны - нуклоны массой 1 а.е.м. с положительным зарядом, равным  единице, то есть элементарному заряду электрона. Нейтроны - электронейтральные нуклоны массой 1 а.е.м.

Свойства:

1) короткодействие: ядерные силы действуют только на малых расстояниях, сравнимых по порядку величины с размерами самих нуклонов.

2) насыщением. Это означает, что любой нуклон ядра взаимодействует не со всеми другими нуклонами, а лишь с ограниченным числом нуклонов, являющихся его непосредственными соседями.

3) равнодействие. Поскольку предполагается, что силы взаимодействия между нуклонами обоих видов являются силами одной природы, то тем самым постулируется, что на равных расстояниях по­рядка 10^{-13 см} два протона, два нейтрона или протон с нейтроном взаимо­действуют одинаково.

49.  Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). Ядро – система связанных нуклонов, состоящая из Z протонов (масса протона в свободном состоянии m_p) и N нейтронов (масса нейтрона в свободном состоянии m_n). Для того, чтобы разделить ядро на составные нуклоны, нужно затратить определенную минимальную энергию W, называемую энергией связи. При этом покоящееся ядро с массой М переходит в совокупность свободных покоящихся протонов и нейтронов с суммарной массой Zm_p + Nm_n. Энергия покоящегося ядра Мс². Энергия освобождённых покоящихся нуклонов (Zm_{p +} Nm_n)с². В соответствии с законом сохранения энергии Мс² + W = (Zm_p + Nm_n)с². Или W = (Zm_p + Nm_n)с² - Мс². Поскольку W > 0, то М < (Zm_p + Nm_n), т.е. масса, начального ядра, в котором нуклоны связаны, меньше суммы масс свободных нуклонов, входящих в его состав.

50. Ядерные силы силы — удерживающие нуклоны (протоны и нейтроны) в ядре. Они действуют только на расстояниях не более 10 ^-13 см и достигают величины, в 100-1000 раз превышающей силу взаимодействия электрических зарядов.

Ядерные силы не зависят от заряда нуклонов. Они обусловлены сильным взаимодействием.

Сведения о ядерный силах были получены из данных о рассеянии нуклонов на нуклонах, а также из исследований свойств атомных ядер (связанных состояний нуклонов). Само существование атомных ядер заставляет предположить, что в ядерных силах имеется существенное притяжение, которое и обеспечивает энергию связи нуклонов в ядрах порядка нескольких МэВ на нуклон. Кроме того, с увеличением числа нуклонов A в ядре энергия связи на нуклон остается примерно постоянной, а объем ядра растет пропорционально A. Про системы с такими свойствами говорят, что в них имеется насыщение сил, и потому ядерные силы называют насыщающими. Они приводят к возможности существования ядерной материи (Нейтронные звезды), плотность энергии которой не зависит от полного числа нуклонов и составляет примерно 16 МэВ на нуклон (если пренебречь электромагнитными (кулоновским) и гравитационными взаимодействиями). В общем случае можно представить себе, что ядерные силы – это притяжение только между нуклонами — ближайшими соседями, поэтому и энергия связи ядра пропорциональна числу нуклонов в ядре.

51. Ядерная реакция – это процесс взаимодействия атомного ядра с другим ядром или элементарной частицей, сопровождающийся изменением состава и структуры ядра и выделением вторичных частиц или γ-квантов.

В результате ядерных реакций могут образовываться новые радиоактивные изотопы, которых нет на Земле в естественных условиях.

Первая ядерная реакция была осуществлена Э. Резерфордом в 1919 году в опытах по обнаружению протонов в продуктах распада ядер (см. § 6.5). Резерфорд бомбардировал атомы азота α-частицами. При соударении частиц происходила ядерная реакция, протекавшая по следующей схеме: 

При ядерных реакциях выполняется несколько законов сохранения: импульса, энергии, момента импульса, заряда. В дополнение к этим классическим законам при ядерных реакциях выполняется закон сохранения так называемого барионного заряда (т. е. числа нуклонов – протонов и нейтронов). Выполняется также ряд других законов сохранения, специфических для ядерной физики и физики элементарных частиц.

Ядерные реакции могут протекать при бомбардировке атомов быстрыми заряженными частицами (протоны, нейтроны, α-частицы, ионы). Первая реакция такого рода была осуществлена с помощью протонов большой энергии, полученных на ускорителе, в 1932 году: 

52. Цепна́я я́дерная реа́кция — последовательность единичных ядерных реакций, каждая из которых вызывается частицей, появившейся как продукт реакции на предыдущем шаге последовательности. Примером цепной ядерной реакции является цепная реакция деления ядер тяжёлых элементов, при которой основное число актов деления инициируетсянейтронами, полученными при делении ядер в предыдущем поколении.

53. Термоядерная реа́кция — разновидность ядерной реакции, при которой лёгкие атомные ядра объединяются в более тяжёлые за счет кинетической энергии их теплового движения.

54. Радиоактивность — спонтанное испускание ионизирующего излучения нестабильными атомными ядрами в результате ядерного распада или квантового перехода на более низкий энергетический уровень.

Радиоактивность следует отличать от ядерных реакций, происходящих вследствие поглощения ядром-мишенью ядерной частицы (нейтрона, протона, α-частицы) и образования составных ядер. Время жизни составных ядер может достигать величины 10⁻¹⁴-10⁻¹² секунда, что гораздо больше времени пролёта ядерной частицы ядра (10⁻²²-10⁻²¹ с). Условной границей времени жизни радиоактивных ядер считается 10⁻¹² с (1 пс).

55. Закон радиоактивного распада — физический закон, описывающий зависимость интенсивности радиоактивного распада от времени и количества радиоактивных атомов в образце. Открыт Фредериком Содди и Эрнестом Резерфордом, каждый из которых впоследствии был награжден Нобелевской премией. Они обнаружили его экспериментальным путём и опубликовали в 1903 году в работах «Сравнительное изучение радиоактивности радия и тория»^[1] и «Радиоактивное превращение»^[2], сформулировав следующим образом^[3]:

Во всех случаях, когда отделяли один из радиоактивных продуктов и исследовали его активность независимо от радиоактивности вещества, из которого он образовался, было обнаружено, что активность при всех исследованиях уменьшается со временем по закону геометрической прогрессии.

56. Элемента́рная части́ца — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить на составные части.

Следует иметь в виду, что некоторые элементарные частицы (электрон, фотон, кварки и т. д.) на данный момент считаются бесструктурными и рассматриваются как первичныефундаментальные частицы. Другие элементарные частицы (так называемые составные частицы — протон, нейтрон и т. д.) имеют сложную внутреннюю структуру, но, тем не менее, по современным представлениям, разделить их на части невозможно (см. Конфайнмент).

Строение и поведение элементарных частиц изучается физикой элементарных частиц.