
2. Работа в аудитории
2.1. Анализ примеров
Пример 1. Исследовать устойчивость системы с характеристическим полиномом
![]()
с помощью критерия Гурвица.
Решение. Для оценки устойчивости по критерию Гурвица необходимо из коэффициентов характеристического уравнения составить определитель по следующим правилам:
– по главной диагонали выписываются все коэффициенты характеристического уравнения от а1 до аn в порядке возрастания индексов;
– столбцы определителя заполняются коэффициентами от главной диагонали вниз по убывающим, а вверх – по возрастающим индексам;
– места коэффициентов, индексы которых больше n или меньше нуля заполняются нулями.
Для характеристического
полинома
![]() составим
определитель Гурвица в общем виде:
составим
определитель Гурвица в общем виде:
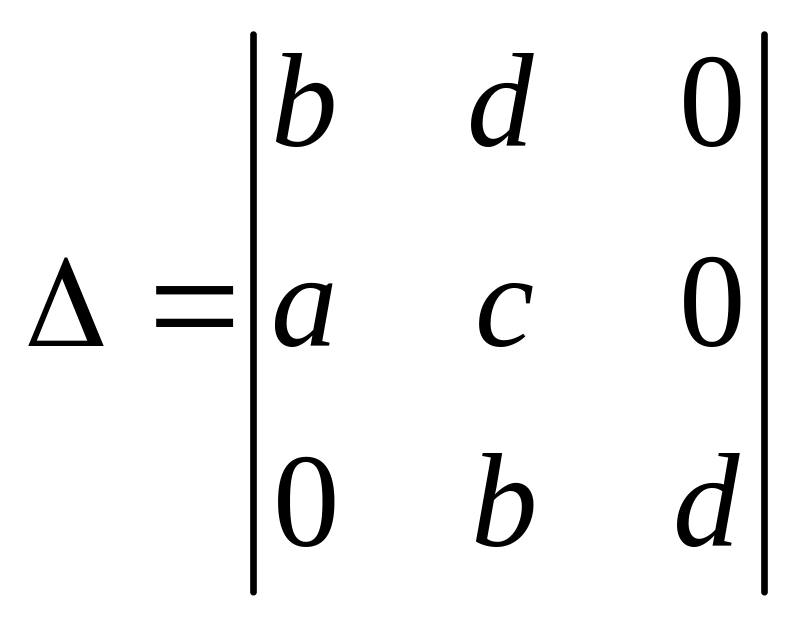 .
.
Для того, чтобы все корни характеристического уравнения имели отрицательные вещественные части и система была устойчивой, необходимо и достаточно, чтобы все диагональные определители определителя Гурвица были строго больше нуля. Если хотя бы один из определителей меньше нуля, то система неустойчива.
Таким образом, необходимо, чтобы
![]() ;
;
![]() ;
;
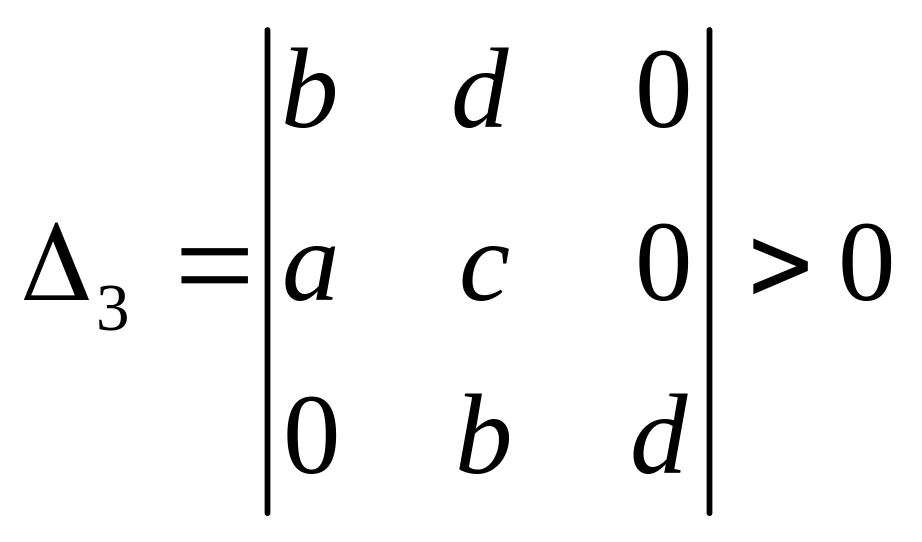 .
.
Оценим устойчивость заданной системы:
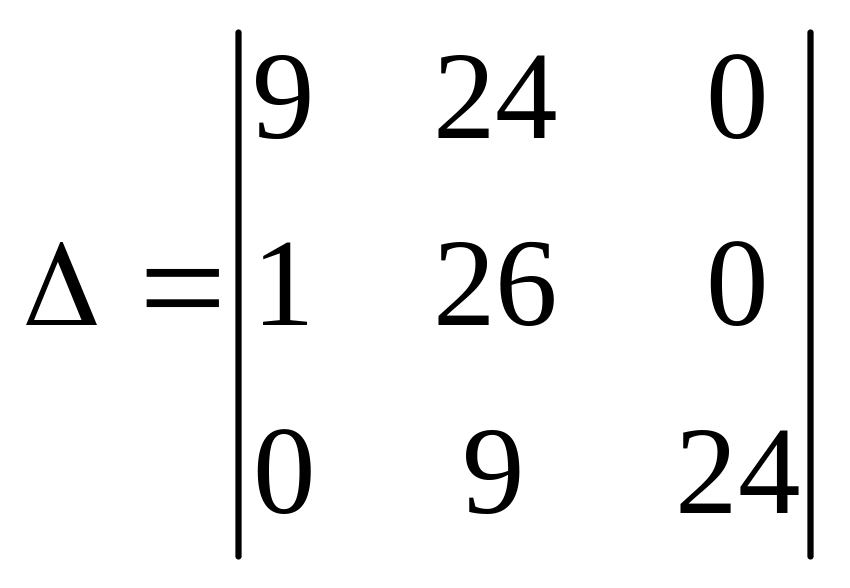
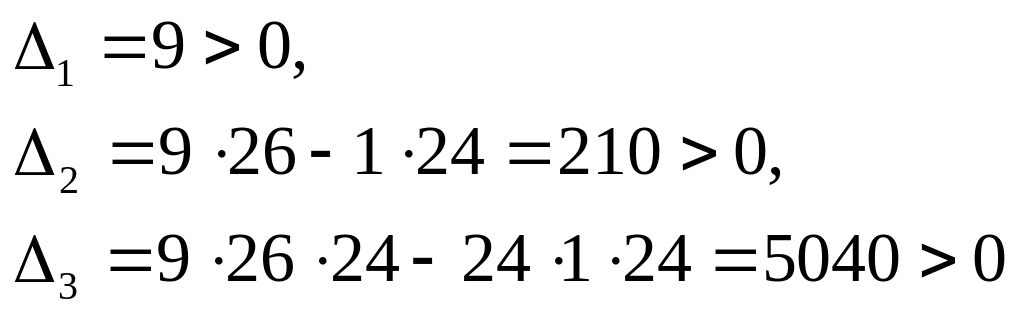 .
.
Таким образом, все диагональные определители определителя Гурвица, больше нуля, следовательно, система с характеристическим полиномом устойчива.
Пример 2. Исследовать на устойчивость систему с характеристическим полиномом
![]()
с помощью критерия Рауса.
Решение. Составим таблицу Рауса для системы с заданным характеристическим полиномом:
|
|
|
|
|
|
|
|
0 |
|
|
0 |
Для устойчивости системы автоматического регулирования необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса были положительны.
В нашем случае это условие выполняется, следовательно, система устойчива.
Пример 3. Для системы, структурная схема которой представлена на рис. 3,

Рис. 3. Структурная схема системы
построить область устойчивости в функции коэффициентов усиления Ку1 и К0 , если остальные параметры равны:
![]() ,
,
т.е. определить такие значения коэффициентов усиления Ку1 и К0, при которых система находится на границе устойчивости.
Решение. Передаточная функция разомкнутой системы имеет вид:
![]() .
.
Найдем передаточную функцию замкнутой системы, при W2 = 1:
![]()
где
![]()
Характеристическое уравнение имеет вид
![]() ,
,
![]()
![]()
Пользуясь критерием Гурвица, имеем
![]() (20)
(20)
Условия (20) выполняются при К0 > 0 , Ку2 > 0. Получим:
![]() .
.![]()
Граница устойчивости определяется выражением
![]()
Область устойчивости в плоскости параметров Кy1 и К0 построена на рис. 4.

Рис 4. Область устойчивости в плоскости параметров Кy1 и К0
Таким образом, при выборе параметров системы Кy1 и К0 (а это необходимо, например, для увеличения точности) необходимо выбирать такие их значения, которые бы находились в заштрихованной области рис. 4. В противном случае система будет неустойчивой.
