Практическое занятие №6
Устойчивость систем управления. Алгебраические критерии
устойчивости
Цель: Получение практических навыков оценки устойчивости систем управления с использованием алгебраических критериев
1. Основные теоретические сведения
1.1. Математические аспекты понятия устойчивости
Общие положения. В практических задачах, сводящихся к интегрированию дифференциальных уравнений, важным является исследование влияния на решение уравнения:
– начальных условий;
– внешних (управляющих и возмущающих) воздействий.
Исходные понятия, относящиеся к этим задачам, сводятся к следующему.
Начальные условия являются обычно результатом измерений и потому содержат некоторую погрешность. Поэтому возникает вопрос о влиянии малых изменений начальных условий на искомое решение дифференциального уравнения. Если малые изменения начальных условий способны сильно изменить решение, то дифференциальное уравнение при неточно измеренных начальных значениях не будет даже приближенно описывать изучаемое явление, т.е. не будет иметь практического значения. Следовательно, практически важным является вопрос о нахождении условий, при которых малое изменение начальных условий вызовет столь же малое изменение решения дифференциального уравнения, т.е. решение дифференциального уравнения мало зависит от значений начальных условий.
Пусть для дифференциального уравнения первого порядка
(1)
существует решение
,
определяемое
начальным условием
,
и решение
,
соответствующее измененному начальному
условию
.
Предполагается также, что решения
и
определены для всех
.
Решение
устойчиво в
смысле Ляпунова,
если из того, что для любого
существует
такое, что из неравенства
,
следует, что
.
Если решение
устойчиво и существует
такое, что из неравенства
следует, что
,
то решение называется асимптотически устойчивым.
Аналогично определяются понятия устойчивости и асимптотической устойчивости для систем дифференциальных уравнений первого порядка.
Практическое
значение второй
задачи
состоит в том, чтобы при упрощении правой
части дифференциального уравнения,
т.е.
,
выбрать действительно наиболее
существенные факторы, оказывающие
наибольшее влияние на изучаемое явление.
Тогда простота решения будет совпадать
с его адекватностью природе изучаемого
явления.
Исследование на
устойчивость произвольного решения
дифференциального уравнения (1) путем
замены переменных вида
может быть сведено к исследованию на
устойчивость нулевого (тривиального)
решения
.
В дальнейшем задача исследования на
устойчивость решается именно для этого
решения.
Устойчивость решений дифференциальных уравнений. Общее решение однородного линейного дифференциального уравнения n-го порядка с непрерывными коэффициентами
имеет вид
,
где
– произвольные постоянные, а
,
,…,
– линейно независимые частные решения.
Признаком линейной независимости частных решений является неравенство нулю определителя Вронского:
.
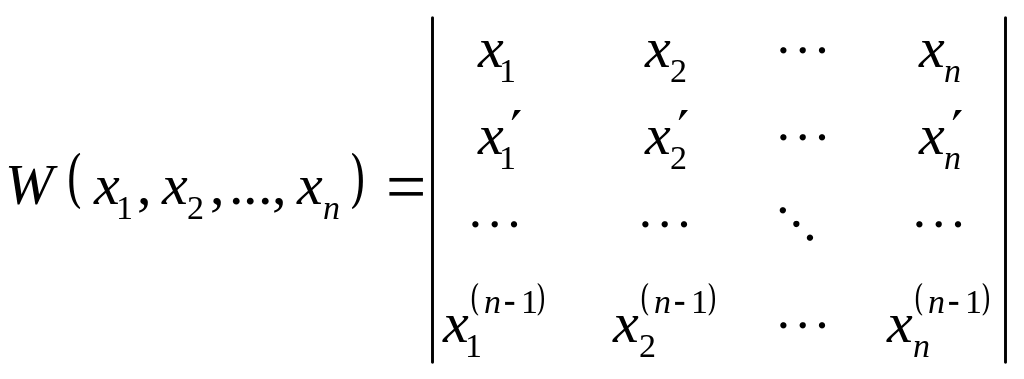Нахождение частных решений однородных и неоднородных линейных дифференциальных уравнений является обычно сложной задачей. Тем не менее, существуют виды дифференциальных уравнений, для которых она решается сравнительно легко. К их числу относятся уравнения с постоянными коэффициентами, т. е. уравнения вида
, (2)
для которых частные
решения можно искать в виде
.
Дифференцируя это решение, подставляя
в (2) и сокращая все на
,
получим так называемое характеристическое
уравнение
.
Если все корни
различны, то все частные решения
линейно независимы, и, следовательно,
общим решением является
.
Пример 1. Найти общее решение уравнения
.
Решение. Корнями характеристического уравнения
являются
и
.
Следовательно, общее решение имеет вид
.
■
Если среди корней
есть кратные, то корню кратности r
соответствует r
решений вида
.
При этом общее решение приобретает вид
, (3)
где m
– число различных корней характеристического
уравнения, а
– многочлен с произвольными коэффициентами
степени на единицу меньше кратности
корня
(для простого корня кратность
и
).
Пример 2. Найти общее решение уравнения
.
Решение. Характеристическое уравнение
или
имеет трехкратный
корень
.
Следовательно, общее решение представляется
выражением
.
■
Если характеристическое уравнение имеет комплексные корни, то его решение можно записать в виде (3) либо с помощью формул Эйлера в действительной форме. Это основано на известном соотношении между декартовым и полярным представлением комплексных чисел.
Известно, что если
уравнение (1) имеет комплексное решение
,
то действительная и мнимая части этого
решения также являются решениями этого
же уравнения. Поэтому соответствующее
паре комплексных корней
комплексное решение
может быть заменено действительными решениями
и
.
В случае кратных комплексных корней решения вида
заменяется решениями
и
.
Пример 3. Общее решение уравнения
может быть представлено в виде
либо в виде
.
■
Устойчивость решения системы дифференциальных уравнений. Частные решения однородной линейной системы дифференциальных уравнений с постоянными коэффициентами
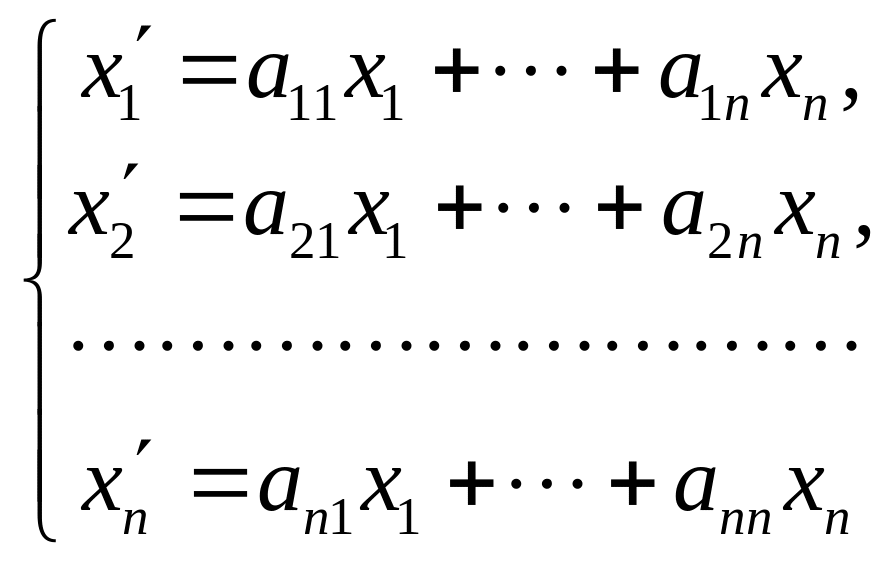(4)
можно искать в виде
,
,…,
.
Подставляя эти значения в исходную систему, сокращая на и перенося все члены каждого уравнения в одну часть равенства, получим
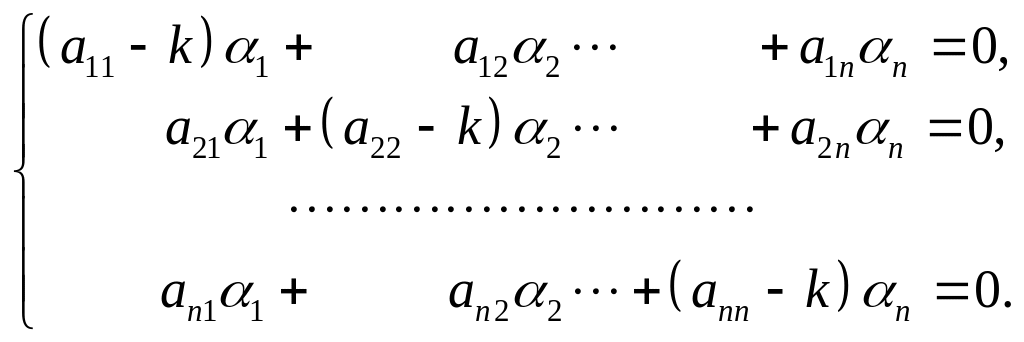(5)
Для того, чтобы
эта система имела ненулевое решение
(т.е. обращалась в нуль, когда не все
имеют нулевые значения), определитель
ее должен быть равным нулю
.
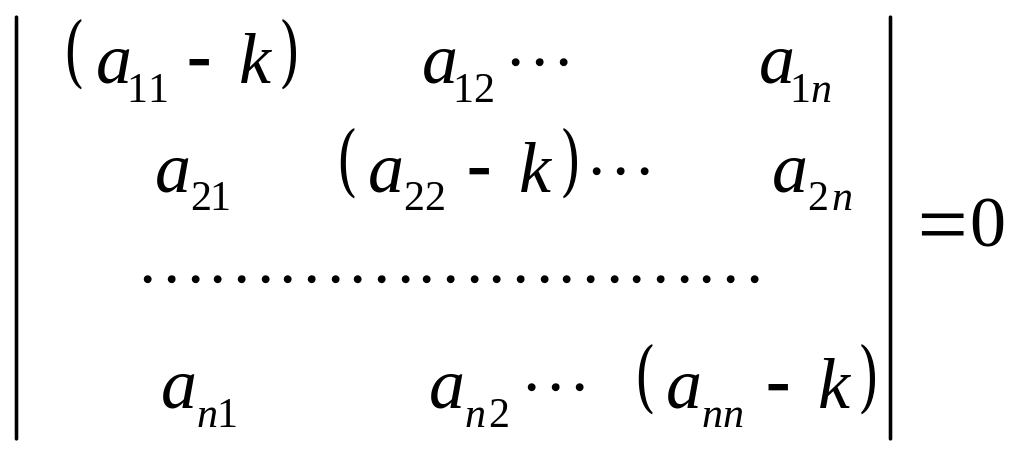Вид решения системы (4) зависит от характера корней характеристического уравнения. Если корни различны, то, подставляя в (5) поочередно корень ki, найдем соответствующие значения
,
,…,
и тем самым находим решение исходной системы
,
,…,
.
(6)
Пример 4. Найти общее решение системы дифференциальных уравнений
(7)
Решение. Будем искать решение в виде
,
.
Подставляя выражения для переменных и
их производных в исходную систему,
получим систему уравнений для определения
и
.
Определяем k из уравнения
,
откуда
,
.
Тогда для определения
и
при
получим
Поскольку второе
уравнение является следствием первого,
то
можно
взять произвольным, например,
,
тогда
и решением исходной системы уравнений
является, например
,
.
Аналогично, при
получим
Отсюда следует,
что
и если принять
,
тогда
.
Это позволяет записать решение системы
в виде
,
.
Следовательно, общее решение системы (7) может быть записано в виде
,
.
■
Если характеристическое уравнение имеет некоторый корень кратности r, то соответствующее ему решение системы (4) можно искать в виде
,
,
(8)
где многочлены
вычисляются путем подстановки
в (4).
При наличии комплексных корней можно преобразовать решения видов (6) или (8) по формулам Эйлера, как и в случае одиночного дифференциального уравнения.
Пусть
,
,…,
есть решение системы дифференциальных уравнений
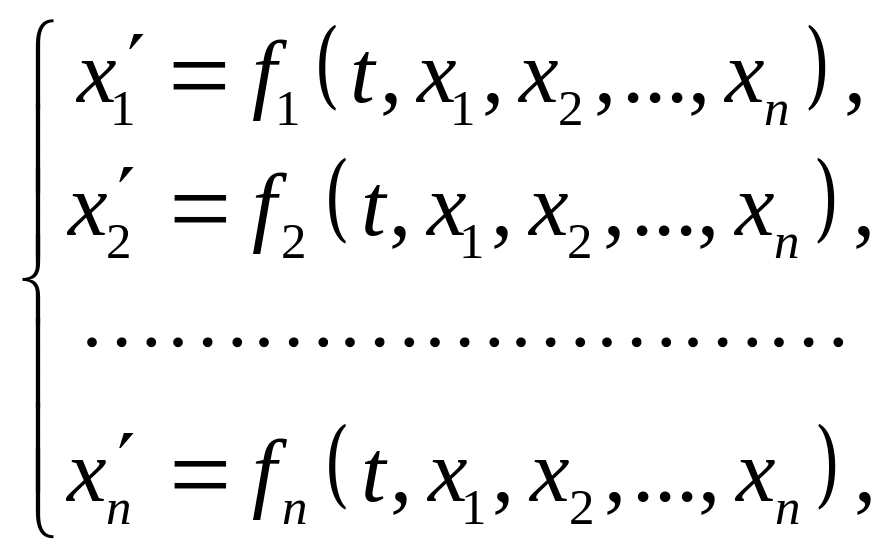(9)
определяемое начальными условиями
,
,…,
,
а
,
,…,
есть решение, соответствующее измененным начальным условиям
,
,…,
.
Тогда решение
называется устойчивым
в смысле Ляпунова,
если для любого
существует такое
,
что из совокупности неравенств
следуют неравенства
,
.
Решение
называется асимптотически устойчивым,
если оно устойчиво и решения
,
достаточно близкие к решению
по начальным значениям
,
неограниченно сближаются с ростом t.
Наконец, решение называется асимптотически устойчивым в целом, если
при любых
начальных значениях
.
Решения, не
обладающие свойством устойчивости,
называются неустойчивыми. Например,
решение
уравнения
устойчиво при
,
асимптотически устойчиво (и асимптотически
устойчиво в целом) при
и неустойчиво при
.
Действительно,
решение рассматриваемого уравнения
при начальном условии
есть
.
(10)
Отсюда при имеем:
– устойчивость:
при
,
следовательно
,
если
;
– асимптотическая
устойчивость:
при
и при любом
получаем, что
;
– асимптотическая
устойчивость в целом:
при
при
любых
и
;
– неустойчивость:
при
для сколь угодно малого (но не равного
нулю!)
решение
с ростом t
не может удовлетворять условию
.
Семейства
интегральных кривых, соответствующих
множествам возможных решений системы
(9) при различных значениях
,
приведены на рис. 1.
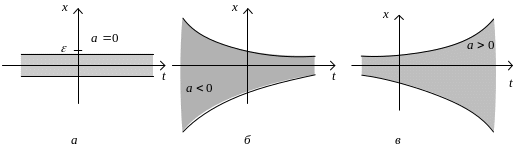
Рис. 1. Семейства интегральных кривых-решений
Системы дифференциальных уравнений (9)
Решение можно
рассматривать как закон
движения в
-мерном
пространстве координат
.
Набор конкретных законов изменения
переменных определяет траекторию
движения, а набор конкретных значений
этих переменных – точку
покоя системы.
Вместо использования
в качестве исходного решения тривиального
решения
и
соответствующего ему определения
устойчивости часто используют следующее
эквивалентное определение: точка покоя
называется
устойчивой, если для каждого
существует такое
,
что из неравенства
следует неравенство
(т.е. если начальная точка находится
внутри
n-мерного
шара радиуса
с центром в начале координат, то при
траектория не выйдет за пределы шара
радиуса
с тем же центром).
Устойчивость
линейных систем с постоянными
коэффициентами.
Условием устойчивости решений линейного
дифференциального уравнения первого
порядка с постоянными коэффициентами
в соответствии с (10) является условие
или, что то же самое, отрицательность
корня характеристического уравнения
.
Для оценки устойчивости системы двух уравнений с постоянными коэффициентами
(11)
с решением
,
поступают следующим образом. Подставляя искомые решения в исходную систему и сокращая на , получаем для определения и систему уравнений
для нетривиальности решения которой ее определитель должен быть равен нулю:
.
Отсюда определяются значения k, т.е. k1 и k2.
Если
,
то определяются соответствующие им две
пары значений
и
,
т.е.
и
и получаем общее решение системы (11) в
виде
(11, а)
. (11,
б)
Это же решение можно записать и в действительной форме
,
где
и
– некоторые линейные комбинации
произвольных постоянных
и
.
Рассмотрим возможные виды решений системы в зависимости от сочетания значений корней характеристического уравнения. Возможны следующие случаи:
1.
,
2.
,
3.
,
4.
.
В первом
случае точка
покоя
асимптотически устойчива в целом, так
как при любых значениях
и
все решения при
стремятся к нулю.
Рассмотрим поведение
траекторий с изменением
.
С ростом
точки любой траектории приближаются к
точке покоя. Две траектории, соответствующие
значениям произвольных постоянных
и
– прямые линии (не зависящие от параметра
t)
и
,
при этом с ростом t точка (x, y) стремится к началу координат.
Схематическое расположение траекторий в окрестности точки покоя, соответствующее этому случаю, показано на рис.2.
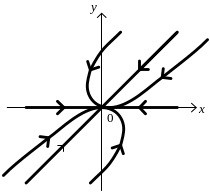
Рис. 2. Расположение траекторий решений системы
Дифференциальных уравнений (11)
Точка покоя в этом случае называется устойчивым узлом.
Во втором случае траектории не изменяются по сравнению с предыдущим случаем (он сводится к предыдущему заменой t на – t), меняется только направление движения. Точка покоя становится неустойчивым узлом.
В третьем
случае из
(11,а)
и (11,б)
следует, что при
и
точка, движущаяся по любой траектории,
удаляется от начала координат, а при
– приближается к началу координат, не
достигая его (начала координат). Точка
покоя такого типа называется седловой,
она является неустойчивой.
Если же
,
то одно из уравнений является следствием
другого и тогда
и
определяются лишь с точностью до
постоянного множителя.
В четвертом случае все решения являются периодическими функциями, а их траектории – замкнутыми кривыми (в общем случае – эллипсами) и асимптотического приближения к началу координат при нет.