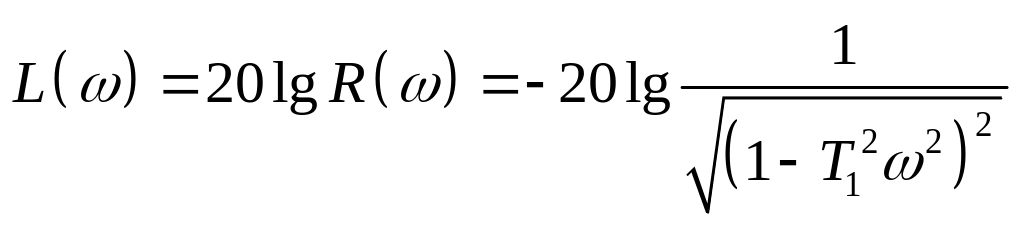Частотные характеристики консервативного звена
Наименование характеристики |
Описание |
Частотная передаточная функция |
|
Действительная часть частотной передаточной функции |
|
Мнимая часть частотной передаточной функции |
|
Модуль частотной передаточной функции |
|
Фазовая частотная характеристика |
|
Логарифмическая амплитудная частотная характеристика |
|
Таблица 8
Частотные характеристики колебательного звена
Наименование характеристики |
Описание |
Частотная передаточная функция |
|
Действительная часть частотной передаточной функции |
|
Мнимая часть частотной передаточной функции |
|
Модуль частотной передаточной функции |
|
Фазовая частотная характеристика |
|
Логарифмическая амплитудная частотная характеристика |
|
Таблица 9
Частотные характеристики апериодического звена 2-го порядка
Наименование характеристики |
Описание |
Частотная передаточная функция |
|
Действительная часть частотной передаточной функции |
|
Мнимая часть частотной передаточной функции |
|
Модуль частотной передаточной функции |
|
Фазовая частотная характеристика |
|
Логарифмическая амплитудная частотная характеристика |
|
Таблица 10
Частотные характеристики форсирующего звена 2-го порядка
Наименование характеристики |
Описание |
Частотная передаточная функция |
|
Действительная часть частотной передаточной функции |
|
Мнимая часть частотной передаточной функции |
|
Модуль частотной передаточной функции |
|
Фазовая частотная характеристика |
|
Логарифмическая амплитудная частотная характеристика |
|
2. Работа в аудитории
2.1. Анализ примеров
Пример 1. Задана функция
,
где
.
Найти соответствующее ей преобразование
Фурье.
Решение. Вначале находим преобразование Лапласа
.
Заменяя
на
,
получим преобразование Фурье
.
Амплитудный спектр
изображения Фурье для
есть
,
а его фазовый спектр
.
Пример 2.
Пусть
есть единичный импульс длительности
:
.
Определить Фурье-изображение для этой функции.
Решение.
Изображение Лапласа этой функции можно
получить как разность изображений
единичной функции в момент
и той же функции, сдвинутой на
,
т.е.
.
Поскольку при
,
то ее Фурье-преобразование существует
и может быть получено заменой в
преобразовании Лапласа переменной
на
:
.
Графическое изображение амплитудного спектра приведено на рис. 3.1.
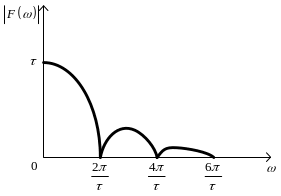
При построении фазового спектра необходимо иметь в виду, что если
,
то
и
.
Если же
,
то
и
.
Пример 3. Для объекта, заданного передаточной функцией 1-го порядка
найти амплитудную частотную характеристику и простроить ее график.
Решение.
Найдем комплексный коэффициент передачи.
Выполним замену
.
Тогда:
.
Выделим действительную и мнимую части, для этого умножим числитель и знаменатель на комплексно-сопряженное знаменателю число:
;
;
;
;
Таким образом, получили:
;
Найдем амплитудно-частотную характеристику, по формуле:
Построим график АЧХ. Найдем несколько точек графика:
;
;
;
;
;
.
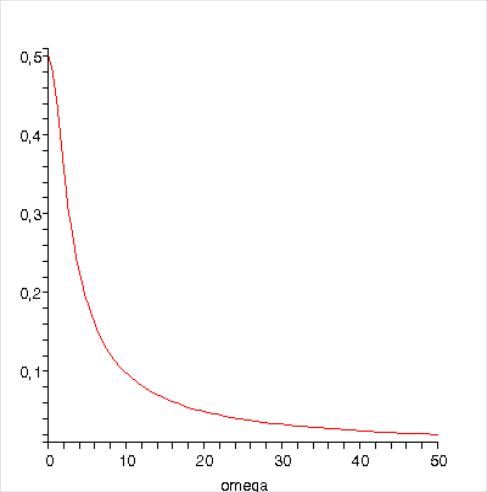
Таким образом,
амплитудно-частотная характеристика
начинается с точки (0, 0,5) и стремится к
(
,
0). С учетом найденных точек выстроим
АЧХ.
Пример 4. Для объекта, заданного передаточной функцией 2-го порядка
найти амплитудную частотную характеристику и простроить ее график.
Решение. Найдем комплексный коэффициент передачи. Выполним замену .
Выделим действительную и мнимую части, для этого умножим числитель и знаменатель на комплексно-сопряженное знаменателю число:
.
Таким образом, получили:
;
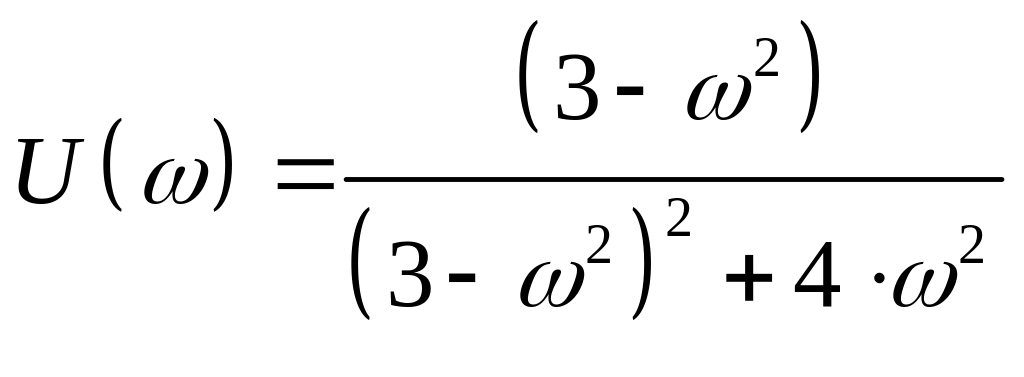Найдем амплитудно-частотную характеристику, по формуле:
,
т.е. имеем:
Построим график АЧХ. Найдем несколько точек графика:
;
;
;
;
;
.
Таким образом, амплитудно-частотная характеристика начинается с точки (0, 1/3) и стремится к ( , 0). С учетом найденных точек выстроим АЧХ.
Пример 5. Для объекта, заданного передаточной функцией 1-го порядка
найти амплитудную частотную характеристику и простроить ее график.
Решение. Найдем комплексный коэффициент передачи. Выполним замену .
Тогда:
.
Выделим действительную и мнимую части, для этого умножим числитель и знаменатель на комплексно-сопряженное знаменателю число:
;
;
Таким образом, получили:
;
;
Найдем амплитудно-частотную характеристику, по формуле:
,
т.е. имеем:
;
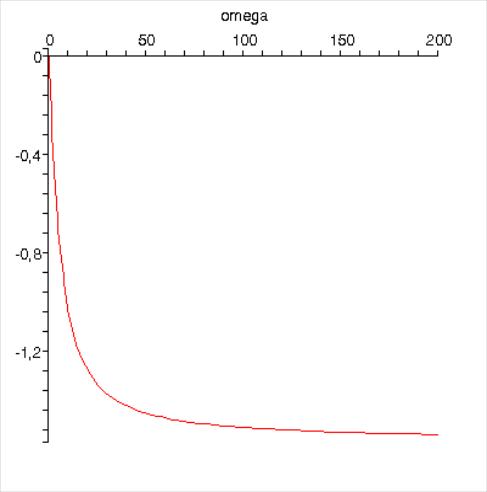
Построим график ФЧХ. Найдем несколько точек графика:
;
;
;
;
;
.
Таким образом, фазовая частотная характеристика начинается с точки (0, 0) и стремится к ( , –1,57). С учетом найденных точек выстроим ФЧХ.
Пример 6. Для объекта, заданного передаточной функцией 2-го порядка
найти амплитудную частотную характеристику и простроить ее график.
Решение. Найдем комплексный коэффициент передачи. Выполним замену .
Тогда
;
Выделим действительную и мнимую части, для этого умножим числитель и знаменатель на комплексно-сопряженное знаменателю число:
;
;
;
Таким образом, получили:
;
;
Найдем амплитудно-частотную характеристику, по формуле:
,
т.е. имеем:
;
Построим график фазовой частотной характеристики. Найдем несколько точек графика:
;
;
;
;
;
.
Таким образом, фазовая частотная характеристика начинается с точки (0, 0) и стремится к ( , -3,14). С учетом найденных точек выстроим ФЧХ.
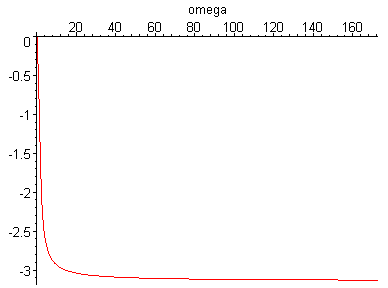
Примечание: Для более детального построения графиков следует брать около 10 точек.
Пример 7. Для объекта, заданного передаточной функцией 2-го порядка
найти годограф и простроить его график.
Решение. Передаточная функция взята из предыдущей задачи, где мы уже выделили действительную и мнимую части комплексного коэффициента передачи:
; ;
Построим годограф. Найдем несколько точек:
;
;
;
;
;
.
;
;
;
;
;
.
С учетом найденных точек строим годограф комплексного коэффициента передачи:
