
П.6 непрерывность функции двух переменных
ОПРЕДЕЛЕНИЕ:
Функция
или
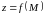 называется непрерывной в точке
,
если она
называется непрерывной в точке
,
если она
определена в этой точке и некоторой ее окрестности
имеет предел
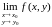
И этот предел равен значению функции в этой точке
 или
или

Функция непрерывная в каждой точке некоторой области называется непрерывной в этой области.
Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке) называются точками разрыва.
Точки разрыва функции могут образовывать целые линии разрыва.
Так
функция
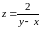 имеет линию разрыва
имеет линию разрыва
 .
.
П.7. Частные производные
Дадим
аргументу
приращение
 ,
а
приращение
,
а
приращение
 ,
тогда функция
получит наращенное значение
,
тогда функция
получит наращенное значение
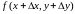 .
.
Величина
 -
называется полным приращением функции
в точке с координатами
.
-
называется полным приращением функции
в точке с координатами
.
Если
задать только приращение по
:
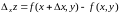 или
только приращение по
:
или
только приращение по
:
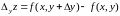 , то полученные приращения функции
называют частными приращениями.
, то полученные приращения функции
называют частными приращениями.
Полное приращение функции, вообще говоря, не равно сумме частных, т.е.

ПРИМЕР:
Найти частное и полное приращение
функции

РЕШЕНИЕ:
 и
и

Теперь посмотрим чему равно полное приращение функции:
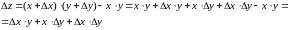
Получили, что
ОПРЕДЕЛЕНИЕ: Частной производной нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю ( если этот предел существует)
Обозначается
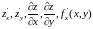
Таким
образом


П.8 частные производные высших порядков
Частные
производные
 и
и
 называют частными производными первого
порядка. Их можно рассматривать как
функции от
.
Эти функции тоже могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:
называют частными производными первого
порядка. Их можно рассматривать как
функции от
.
Эти функции тоже могут иметь частные
производные, которые называются частными
производными второго порядка. Они
определяются и обозначаются следующим
образом:


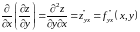

Аналогично
определяются частные производные 3-го,
4-го и т.д. порядков. Так
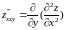 ,
,
 .
.
ПРИМЕР: Найти частные производные второго порядка функции

РЕШЕНИЕ:
Так
как
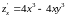 ,
а
,
а

Получаем
 и
и
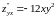
Получили,
что
 .
.
Этот результат не случаен, оказывается справедлива следующая теорема:
ТЕОРЕМА: (ШВАРЦА) Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для имеем
