Лекция «функции нескольких переменных» п 1. Определение функции нескольких переменных

Понятие функции одной переменной не охватывает все зависимости, которые существуют в природе. Даже в самых простых задачах встречаются величины, значения которых определяются совокупностью значений нескольких величин.

1) - площадь прямоугольника является функцией двух переменных, длины и ширины.

2) , скорость равномерного прямолинейного движения есть функция двух переменных пройденного пути и времени.

3) - объем прямоугольного параллелепипеда, определяется совокупностью 3 значений длины, ширины и высоты.

4) изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами: , ,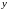 . Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных:  , , . Если физическое состояние тела к тому же еще и меняется с течением времени 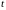 , то та же плотность будет зависеть уже от значений четырех переменных:  , , , .

5) рассмотрим издержки производства на изготовление единицы некоторого вида продукции. Пусть:   - затраты по материалам,  - расходы на выплату заработной платы работникам,  - амортизационные отчисления. Очевидно, что издержки производства зависят от значений названных параметров  , , .

В связи с вышеперечисленными примерами, становится естественным расширение известного понятия функциональной зависимости и введение понятия функции нескольких переменных.

Мы будем рассматривать функции двух переменных, т.к. все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. И эти факты обобщаются на случай большего числа переменных. Кроме того для функций двух переменных можно дать наглядную геометрическую интерпретацию.

Пусть задано множество упорядоченных пар чисел . Соответствие , которое каждой паре чисел сопоставляет одно и только одно число , называется функцией двух переменных, определенной на множестве со значениями во множестве , и записываются в виде или . При этом и называются независимыми переменными (аргументами), а - зависимой переменной (функцией).

Множество называется областью определения функции. Множество значений, принимаемых в области определения, называется областью изменения этой функции, обозначается или .

Так в 1 примере: ( - площадь прямоугольника является функцией двух переменных, длины и ширины), областью определения функции является множество.

Символически функция двух переменных обозначается так: , , и т.д.

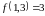Если , то , и т.д.

Как известно, пара чисел и , определяет положение точки 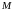на плоскости и, значит, радиус вектор, т.к. с каждой точкой на плоскости можно связать радиус вектор (и наоборот). Поэтому функцию двух переменных можно рассматривать либо как функцию точки и писать , либо как скалярную функцию векторного аргумента .

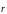
П 2. Способы задания функции .

Как и в случае одной переменой могут быть различными. В виде таблицы, аналитически, графиком. Мы будем пользоваться аналитическим способом задания функции в виде формулы.

ПРИМЕРЫ:

1)

Область определения - вся плоскость (множество всех пар чисел )

Область значений - .

2)

Область определения, множество тех точек, для которых определено выражение , 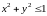- множество всех таких точек образует круг с центром в точке и радиусом .

3) - область определения множество точек, для которых справедливо - это множество точек, лежащих вне круга радиуса 1 с центром в начале координат. Множество значений

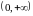
Из рассмотренных примеров видно, что областью определения может быть либо вся плоскость , либо ее часть.