Метод интегрирования по частям

Пусть u = f(x) и v = g(x) - функции, имеющие непрерывные производные. Тогда, по правилу дифференцирования произведения,

d(uv)= udv + vdu или udv = d(uv) -vdu.

Для выражения d(uv) первообразной, очевидно, будет uv, поэтому имеет место формула:

∫ udv = uv - ∫ vdu.                                                       (8.4)

Эта формула выражает правило интегрирования по частям. Оно приводит интегрирование выражения udv=uv'dx к интегрированию выражения vdu=vu'dx.

Пусть, например, требуется найти x cosx dx. Положим u = x, dv = cos x dx, так что du=dx, v=sinx. Тогда

∫ x cos x dx = ∫ x d(sin x) = x sin x - ∫ sin x dx = x sin x + cos x + C.

Правило интегрирования по частям имеет более ограниченную область применения, чем замена переменной. Но есть целые классы интегралов, например,

∫ x^k ln^mx dx, ∫x^k sin bx dx, ∫ x^k cos bx dx, ∫x^k e ^ax dx

и другие, которые вычисляются именно с помощью интегрирования по частям.

Заведение под дифференциал

Из свойства 4.3 также вытекает метод занесения (заведения) под дифференциал — частный случай метода замены переменной, когда явно имеется выражение вида  , которое в свою очередь равно  .

для большого класса выражений.

Приведём несколько примеров.

Пример 5.4. Взять интеграл

Решение. Раскроем гиперболический тангенс через его определение:

Следовательно

Занося под дифференциал  , получаем:

Последнее выражение можно записать по-другому:

где  .

8)Обыкнове́нные дифференциа́льные уравне́ния (оду)

 — это дифференциальное уравнение вида

где   — неизвестная функция (возможно, вектор-функция, тогда  , как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят осистеме дифференциальных уравнений), зависящая от независимой переменной  , штрих означает дифференцирование по  . Число   (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).

Независимая переменная   часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой  . Переменная   — некоторая величина (или совокупность величин, если   является вектор-функцией), изменяющихся со временем. Например,  может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, то есть изменение её координат с течением времени. Независимая переменная   обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная   комплексная (так называемые уравнения с комплексным временем)

• Дифференциальные уравнения первого порядка.

• Простейшие дифференциальные уравнения первого порядка вида 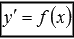 . Запишем несколько примеров таких ДУ  . Дифференциальные уравнения 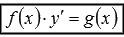  можно разрешить относительно производной, произведя деление обеих частей равенства на f(x). В этом случае приходим к уравнению  , которое будет эквивалентно исходному при f(x) ≠ 0. Примерами таких ОДУ являются 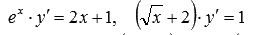 . Если существуют значения аргумента x, при которых функции f(x) и g(x) одновременно обращаются в ноль, то появляются дополнительные решения. Дополнительными решениями уравнения   при данных x являются любые функции, определенные для этих значений аргумента. В качестве примеров таких дифференциальных уравнений можно привести  .  В статье простейшие дифференциальные уравнения первого порядка. Вы можете ознакомиться с подробной теорией и посмотреть примеры решения таких ОДУ.

• Дифференциальные уравнения с разделяющимися переменными вида 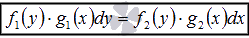  или  . Дифференциальные уравнения   называют уравнениями с разделенными переменными. Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него. Общее решение дифференциальных уравнений с разделенными переменными можно найти, проинтегрировав обе части равенства: ∫ f(y)dy = ∫ f(x)dx.  В качестве примеров ОДУ с разделенными переменными приведем  . Дифференциальные уравнения с разделяющимися переменными приводятся к ОДУ с разделенными переменными делением обеих частей уравнения на произведение f₂(y) ⋅ g₁(x). То есть, получим  . Такое преобразование будет эквивалентным, если одновременно f₂(y) ≠ 0 иg₁(x) ≠ 0. Иначе могут потеряться некоторые решения. Примерами ОДУ с разделяющимися переменными являются  . Некоторые дифференциальные уравнения можно свести к уравнениям с разделяющимися переменными с помощью замены переменных. Дифференциальные уравнения 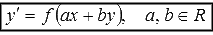  приводятся к ОДУ с разделяющимися переменными подстановкой z = ax+by. К примеру, уравнение   с помощью подстановки z = 2x+3y преобретает вид 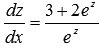 . ОДУ   или   преобразуются к уравнениям с разделяющимися переменными с помощью замен   или 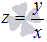 . Например, дифференциальное уравнение  после замены   принимает вид  . Некоторые дифференциальные уравнения следует немного преобразовать, чтобы можно провести замену. К примеру, достаточно разделить на x² или y² числитель и знаменатель правой части дифференциального уравнения  , чтобы оно соответствовало случаям   или   соответственно. Дифференциальные уравнения  преобразуются к только что рассмотренным ОДУ   или  , если ввести новые переменные  , где 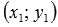  - решение системы линейных уравнений  и провести некоторые преобразования. Например, дифференциальное уравнение 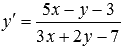  после введения новых переменных   преобразуется к виду  . Проводим деление на u числителя и знаменателя правой части полученного уравнения и принимаем  . В результате приходим к уравнению с разделяющимися переменными  . В разделе дифференциальные уравнения с разделяющимися переменными подробно разобрана теория и приведены подробные решения аналогичных примеров.

• Линейные неоднородные дифференциальные уравнения первого порядка  . В качестве примеров линейных неоднородных дифференциальных уравнений первого порядка можно привести  . Для решения ЛНДУ используют метод вариации произвольной постоянной. Также существует метод, основанный на представлении искомой функции y в виде произведения: y(x) = u(x)v(x). В статье линейные неоднородные дифференциальные уравнения первого порядка подробно изложены методы интегрирования таких ЛНДУ и приведены подробные решения примеров и задач.

• Дифференциальное уравнение Бернулли  . Примерами дифференциальных уравнений Бернулли являются, например,  . Дифференциальное уравнение Бернулли сводится к линейному дифференциальному уравнению первого порядка подстановкой 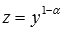 . Можно также пользоваться методом, основанным на представлении функции y как y(x) = u(x)v(x). В разделе дифференциальное уравнение Бернулли подробно расписаны методы нахождения решений и разобраны решения примеров и задач.

• Уравнения в полных дифференциалах 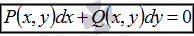 . Если для любых значений x и y выполняется 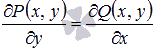 , то этого условия необходимо и достаточно, чтобы выражение P(x, y)dx+Q(x, y)dy представляло собой полный дифференциал некоторой функции U(x, y) = 0, то есть, dU(x, y) = P(x, y)dx + Q(x, y)dy. Таким образом, задача сводится к восстановлению функции U(x, y) = 0 по ее полному дифференциалу. 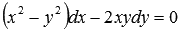К примеру, левая часть дифференциального уравнения   представляет собой полный дифференциал функции  . Подробное описание теории и решение примеров изложены в разделе уравнения в полных дифференциалах

• Дифференциальные уравнения втоого порядка.

  • Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами  . ЛОДУ с постоянными коэффициентами является очень распространенным видом дифференциальных уравнений. Их решение не представляет особой сложности. Сначала отыскиваются корни характеристического уравнения  . При различных p и q возможны три случая: корни характеристического уравнения могут быть действительными и различающимися  , действительными и совпадающими 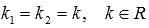  или комплексно сопряженными  . 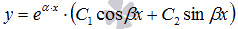В зависимости от значений корней характеристического уравнения, записывается общее решение дифференциального уравнения как  , или  , или  соответственно. Для примера рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами  . Корнями его характеристического уравнения   являются k ₁ = -3 и k ₂ = 0. Корни действительные и различные, следовательно, общее решение ЛОДУ с постоянными коэффициентами имеет вид   Подробное описание теории и разобранные решения примеров и задач смотрите в разделе линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

• Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами  . Общее решение ЛНДУ второго порядка с постоянными коэффициентами y ищется в виде суммы  общего решения соответствующего ЛОДУ   и частного решения   исходного неоднородного уравнения, то есть,  . Нахождению общего решения однородного дифференциального уравнения с постоянными коэффициентами  , посвящен предыдущий пункт. А частное решение   определяется либо методом неопределенных коэффициентов при определенном виде функции f(x), стоящей в правой части исходного уравнения, либо методом вариации произвольных постоянных. В качестве примеров ЛНДУ второго порядка с постоянными коэффициентами приведем 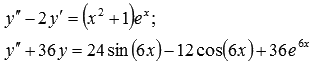  Разобраться в теории и ознакомиться с подробными решениями примеров мы Вам предлагаем на странице линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

• Линейные однородные дифференциальные уравнения (ЛОДУ)   и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка  . Частным случаем дифференциальных уравнений этого вида являются ЛОДУ и ЛНДУ с постоянными коэффициентами. Общее решение ЛОДУ   на некотором отрезке [a; b] представляется линейной комбинацией двух линейно независимых частных решений y ₁ и y ₂ этого уравнения, то есть,  . Главная сложность заключается именно в нахождении линейно независимых частных решений дифференциального уравнения этого типа. Обычно, частные решения выбираются из следующих систем линейно независимых функций:   Однако, далеко не всегда частные решения представляются в таком виде. Примером ЛОДУ является  . Общее решение ЛНДУ 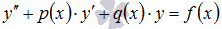  ищется в виде  , где   - общее решение соответствующего ЛОДУ, а   - частное решение исходного дифференциального уравнения. О нахождении   мы только что говорили, а   можно определить, пользуясь методом вариации произвольных постоянных. В качестве примера ЛНДУ можно привести  . Теорию и решение примеров смотрите в разделе линейные дифференциальные уравнения второго порядка. 

• Дифференциальные уравнения высших порядков.

  • Дифференциальные уравнения, допускающие понижение порядка. Порядок дифференциального уравнения  , которое не содержит искомой функции и ее производных до k-1 порядка, может быть понижен до n-k заменой 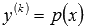 . В этом случае  , и исходное дифференциальное уравнение сведется к  . После нахождения его решения p(x) останется вернуться к замене   и определить неизвестную функцию y. Например, дифференциальное уравнение   после замены   станет уравнением с разделяющимися переменными  , и его порядок с третьего понизится до первого. Если дифференциальное уравнение не содержит аргумента x, то есть, имеет вид  , то его порядок может быть снижен на единицу заменой  , гдеp(y(x)) будет сложной функцией. Тогда по правилу дифференцирования сложной функции получим   и так далее. Подставив эти результаты в исходное уравнение, получаем дифференциальное уравнение не единицу меньшего порядка. К примеру, дифференциальное уравнение   заменой   приводится к уравнению с разделяющимися переменными  . Подробное решение подобных примеров представлено в статье дифференциальные уравнения, допускающие понижения порядка.

  • Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами   и  . Чтобы определить общее решение таких видов дифференциальных уравнений, во-первых, требуется найти корни характеристического уравнения 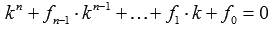 . В этом Вам может помочь статья решение уравнений высших степеней. Далее, отталкиваясь от значений корней характеристического уравнения, общее решение ЛОДУ   записывается в стандартной форме, а общее решение неоднородного уравнения представляется суммой  , где   - частное решение неоднородного дифференциального уравнения.   можно определить методом вариации произвольных постоянных. В качестве примера ЛНДУ с постоянными коэффициентами приведем  , ему соответствует ЛОДУ  . Подробное описание теории и детальный разбор решения примеров смотрите в разделе линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами.

  • Линейные однородные и неоднородные дифференциальные уравнения высших порядков   и  . Общее решение ЛНДУ высших порядков ищется в виде  , где   - общее решение соответствующего ЛОДУ, а   - частное решение неоднородного дифференциального уравнения.  представляет собой линейную комбинацию линейно независимых функций 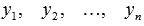 , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство   в тождество. Частные решения   обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема. Когда общее решение линейного однородного дифференциального уравнения найдено, частное решение соответствующего неоднородного уравнения можно определить методом вариации произвольных постоянных. Итак,  . 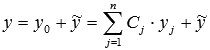Краткое описание теории приведено в статье линейные дифференциальные уравнения высших порядков.

• Системы дифференциальных уравнений вида .