1) Составим, на основании законов Кирхгофа, систему уравнений для расчета токов во всех ветвях цепи и запишем ее в дифференциальной и символической формах.

Дифференциальная форма:

E1m	ф1	Е1`m	ф`1	E2m	ф2	E`2m	ф`2	E3m	ф3	E`3m	ф`3
В	град	В	град	В	град	В	град	В	град	В
								240	45	169	90

В символической форме:

Подставив численные значения, получим:

2)Определим комплексы действующих значений токов, воспользовавшись символическим методом расчета. Запишем выражения для мгновенных значений токов.

Данная цепь является простой разветвленной, она может быть решена методом свертывания. Определим Z эквивалентное:

Подставив численные значения, получим:

;

Определим ток в неразветвленной части цепи.

Определим напряжение на зажимах а, в.

Определим токи в параллельных ветвях.

3) Составим баланс мощностей в комплексной форме, выполнив соответствующие вычисления.

Классический метод.

Определим эквивалентную проводимость параллельных ветвей.

Определим эквивалентные сопротивления ветви а,в.

Град

Определим эквивалентное сопротивление.

;

Определим ток в неразветвленной части ветви и угол между ЭДС E₃ и током I₃.

;

Определим напряжение на зажимах а b.

Определим токи в параллельных ветвях и углы ᵠ.

Баланс мощностей.

;

;

Рассчитаем погрешность при расчете активной мощности:

– в допустимых

пределах.

Рассчитаем погрешность при расчете реактивной мощности:

– в допустимых пределах.

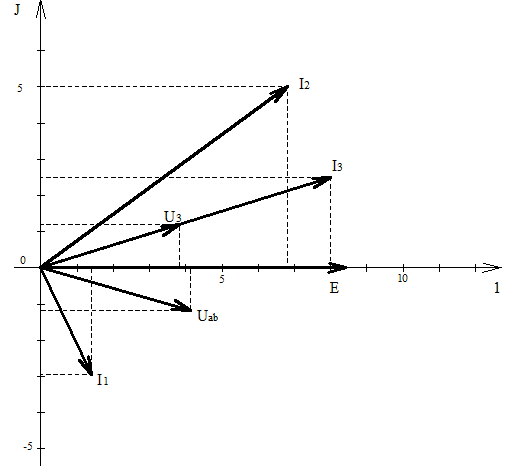
4)Построим на комплексной плоскости векторную диаграмму напряжений и токов.

Задача№3

В трехфазной системе нагрузка соединена в звезду с нейтральным проводом. Определить:

1. Фазные и линейные токи.

2. Угол сдвига фаз между током и напряжением в каждой фазе.

3. Активную, реактивную и полную мощность потребляемую системой.

При обрыве фазы А определить режимы в остальных двух фазах при наличие нейтрального провода и без него.

Для всех случаев построить векторные диаграммы.

UФ	RФ	XLФ	ХСФ
220	36	73	25

Объединение в одну цепь нескольких подобных по структуре цепей синусоидального тока одной частоты с независимыми источниками энергии широко применяются в технике. Объединяемые цепи синусоидального тока принято называть фазами, а всю объединенную систему цепей – многофазной системой. Для получения трехфазной системы необходимо определенным образом соединить фазы источника энергии и приемника. Возможны два способа соединения в трехфазной системе – соединение фаз источника и приемника звездой и треугольником.

И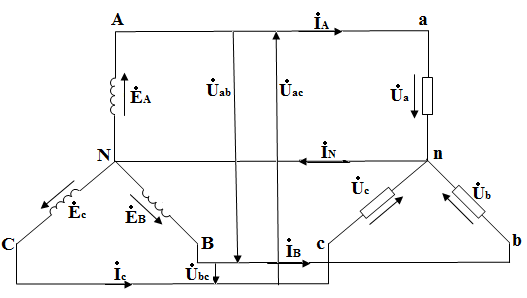 зобразим схему трехфазной системы объединенную в звезду.