
- •Лекции по курсу «Базы данных» для студентов факультета вычислительной математики и кибернетики кгу
- •Системы управления базами данных, их состав и назначение. Файловые и клиент-серверные субд.
- •2. Типы базы данных. Реляционные, иерархические, сетевые, объектно-ориентированные базы данных.
- •Основные понятия теории баз данных. Поиск данных и пользовательские запросы.
- •4. Проектирование предметной области. Объекты и атрибуты предметной области. Связи между объектами типа 1:1, 1:m, m:n.
- •Первичные ключи и индексы
- •Реляционные отношения между таблицами Отношение один-ко-многим
- •Отношение один-к-одному
- •Отношение многие-ко-многим
- •Оператор переименования атрибутов.
- •Теоретико-множественные операторы:
- •Объединение
- •Пересечение
- •3. Вычитание
- •4. Декартово произведение
- •Специальные реляционные операторы
- •5. Выборка (ограничение, селекция)
- •Проекция
- •6. Соединение
- •7. Деление
- •Примеры использования реляционных операторов
- •Кросс-таблицы.
- •Ключи отношений. Их роль и использование в базах данных.
- •Связи между отношениями. Внешние ключи. Проблема целостности внешних ключей.
- •Функциональные зависимости. Аксиоматическая система функциональных зависимостей. Теорема полноты.
- •1. Аксиоматика функциональных зависимостей Армстронга.
- •Покрытия функциональных зависимостей. Структура неизбыточных покрытий.
- •Нормальные формы баз данных. Первая, вторая и третья нормальные формы. Нормальная форма Бойса- Кодда.
- •Вторая Нормальная Форма.
- •Отношение сотрудники_отделы
- •Отношение проекты
- •Отношение задания
- •3 Нормальная форма.
- •Отношение сотрудники
- •Отношение отделы
- •Нормализация баз данных. Алгоритм приведения к 3-й нормальной форме с помощью кольцевых зависимостей.
- •Метод «Entity-Relationship». Проектирование структуры баз данных с помощью er-диаграмм. Пример.
- •Физическая организация баз данных.
- •2. Блочный поиск.
- •3. Двоичный поиск.
- •4. Поиск в индексно-последовательном файле.
- •6. Поиск в сбалансированном дереве.
- •7. Перемешивание.
- •8. Комбинация вышеперечисленных способов.
- •Организация баз данных с помощью хеширования. Влияние на эффективность хеширования размеров блока, плотности заполнения и выбора алгоритма хеширования.
- •2. Деление.
- •3. Сдвиг разрядов.
- •4. Преобразование системы исчисления.
- •Язык sql. Команды create, select, insert, alter, update, drop.
- •Простая выборка
- •Использование операторов сравнения
- •Использование in
- •Использование like
- •Выборка с упорядочением
- •Применение агрегатных функций sum, max, min, average в предложении select.
- •Функции без использования фразы group by
- •Фраза group by
- •Использование фразы having
- •19. Организация сложных запросов с помощью команды select.
- •Декартово произведение таблиц
- •Соединение таблицы со своей копией
- •Простые вложенные подзапросы
- •Объединение (union)
- •Организация клиент–серверных бд. Модели технологий «клиент–сервер».
- •Технологии доступа к данным. Система драйверов odbc. Источники данных. Создание dsn-файла.
- •Модели безопасность данных. Мандатный и дискреционный подход к обеспечению безопасности данных. Передача и отзыв привилегий пользователей с помощью предложения grant.
- •26.Безопасность баз данных. Средства защиты бд access.
- •31. Использование внешних данных в Access. Создание страниц доступа к данным и загрузка внешних баз данных. Выполнение sql-запросов к серверу ms sql Server.
- •I. Создание html-страницы доступа к данным
- •II. Загрузка в Access базы данных c сервера и работа с ней.
- •III. Выполнение в Access запросов к внешним таблицам, хранящимся на ms sql Server.
- •Совместная работа Access и ms sql Server, работа с удаленными данными на сервере. Использование утилиты Query Analyzer.
- •Работа с внешними данными с помощью технологии odbc
- •Команды Transact-sql
- •Создание представлений
- •Создание триггеров
- •37. Raid массивы и уровни их организации.
Функциональные зависимости. Аксиоматическая система функциональных зависимостей. Теорема полноты.
Определения. Пусть A1,A2, ..., An – набор атрибутов с приписанными им доменами D1, D2, ... Dn. Выражение R= < A1,A2, ..., An > называется схемой атрибутов. Любое отношение r с атрибутами из множества R называется отношением над схемой R (обозначается r = r(R)).
Пусть Q- непустое подмножество R, кортеж t принадлежит отношению r(R) , t=<t1, t2, ... , tn>. Ограничением кортежа t на множестве Q называется кортеж t(Q), состоящий из тех значений ti, что iQ.
Определение. Пусть множества А, В R, r – отношение над схемой R. Функциональной зависимостью называется формальное выражение вида AB. Функциональная зависимость AB выполняется в отношении r, если
( t, qr ) t(A)=q(A) t(B)=q(B) (2)
Из определения следует, что если К является ключом r, то в r выполнятся функциональная зависимость КR. Поэтому понятие ключевой зависимости является частным случаем функциональной зависимости.
Рассмотрим в качестве примера отношение Авиарейсы (ПИЛОТ, РЕЙС, ДАТА, ВРЕМЯ ВЫЛЕТА). В этом отношении выполняются следующие ограничения:
Для каждого рейса назначается только одно время вылета.
Для каждого пилота, времени вылета и даты назначается один рейс.
Для каждого рейса и даты назначается один пилот.
Эти ограничения можно записать в виде следующих функциональных зависимостей:
{РЕЙС}{ВРЕМЯ}
{ПИЛОТ, ДАТА, ВРЕМЯ} {РЕЙС}
{РЕЙС, ДАТА}{ПИЛОТ}
Реляционное исчисление. Задача этой части – построить аксиоматическое исчисление функциональных зависимостей, т.е. описать систему аксиом и правил вывода, позволяющих выводить одни ф.з. из других, причем если в отношении r выполняются исходные, то выполняются и производные зависимости. Наша аксиоматика называется системой Армстронга и состоит из одной аксиомы и 3 правил вывода. Для краткости будем называть функциональные зависимости просто формулами.
Определение. Правило

называется допустимым, если для любого отношения r из того что все формулы из F выполняются в r, следует что формула A B также выполняется в r.
В дальнейшем, будем для краткости опускать символ объединения , записывая объединение просто XZ. Это не даст двусмысленности, поскольку операция пересечения множеств у нас использоваться не будет.
1. Аксиоматика функциональных зависимостей Армстронга.
Аксиомы:
Аксиомы: Пусть R—множество атрибутов, AR. Аксиомой является функциональные зависимости вида AA.
Правила вывода:
1) правило накопления
![]()
2) правило проективности
![]()
Определение. Пусть F- множество формул над схемой R, X,YR. Формула XY является логическим следствием набора формул F, если для любого отношения r над схемой R, если все формулы из F выполняются в r , то в r выполняется формула XY. Множество всех логических следствий из F будем обозначать F*.
Определение. Пусть F- множество формул над схемой R. Замыканием F (обозначается [F]) называется множество всех формул, выводимых из F.
Определение. Исчисление называется полным, если для любого множества формул F F* [F]. Исчисление называется непротиворечивым, если [F] F*.
Теорема полноты. Аксиоматика Армстронга является полной и непротиворечивой.
Доказательство. 1. Докажем сначало непротиворечивость. Пусть F – непустое множество формул над схемой R. . Нам надо показать, что любая формула, выводимая из F по правилам Р1, Р5, является логическим слествием. Пусть r- произвольное отношение, в котором выполняются формула XY из F, т.е. ( t, qr ) t(X)=q(X) t(Y)=q(Y). Пусть для кортежей t, qr выполняется t(XZ)=q(XZ), тогда выполняется и t(X)=q(X), и , значит, t(Y)=q(Y). Это означает, что в r выполняется формула XZY. Значит, формулы, выведенные по правилу Р1, являются логическими следствиями F. Аналогично доказывается, что применение правила P5 также дает логические следствия (доказать самостоятельно!) , и первая часть теоремы доказана.
2. Докажем теперь полноту аксиоматики Армстронга. Пусть она – не полна. Тогда существует формула XY, являющаяся логическим следствием F, но не выводимая из F. Заметим, что если из F выводимы формулы XY, XZ, то по правилу аддитивности выводима формула XYZ. Поэтому, найдется некоторое максимальное множество V такое, что XV выводимо из F, и для любого Z, XZ выводимо, влечет ZV. В силу предположения, Y не содержится в V. Определим некоторое отношение r, содержащее два кортежа:
|
|
… |
|
|
|
… |
|
|
|
… |
|
где
![]()
Очевидно, что p(X)=q(X), и p(Y)q(Y), поэтому формула XY не выполняется в r. Покажем, однако, что все формулы из F, выполняются в r. Действительно, пусть формула AB принадлежит [F]. Если A не является подмножеством U, то p(A)q(A), и формула p(A)=q(A) p(В)=q(В) истинна. Если AU, то BU, т.к. выводимо XU, UA, AB и по правилу транзитивности, XB, и в силу выбора U, BU. Таким образом, все формулы из F выполнимы в r, а формула XY не выполняется в r, и, значит, последняя формула не является логическим следствием формул F. Получили противоречие, и теорема доказана.
Доказанная
теорема дает практический способ
проверки выводимости формулы
![]() из набора
из набора
![]() других формул:
других формул:
ищем максимальное
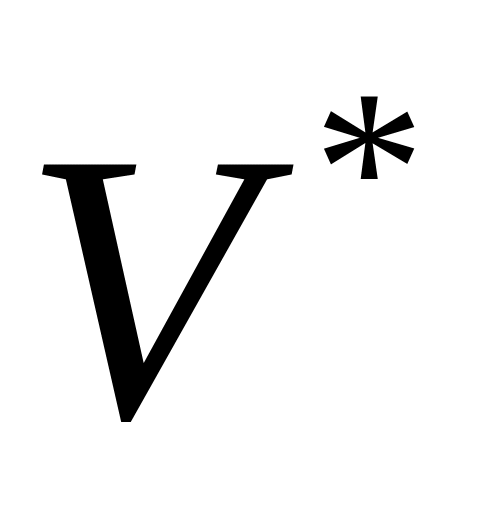 :
:
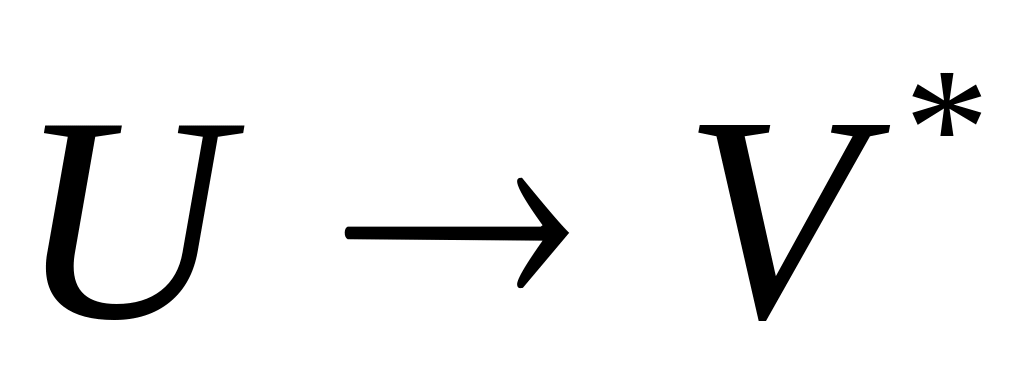
проверяем:
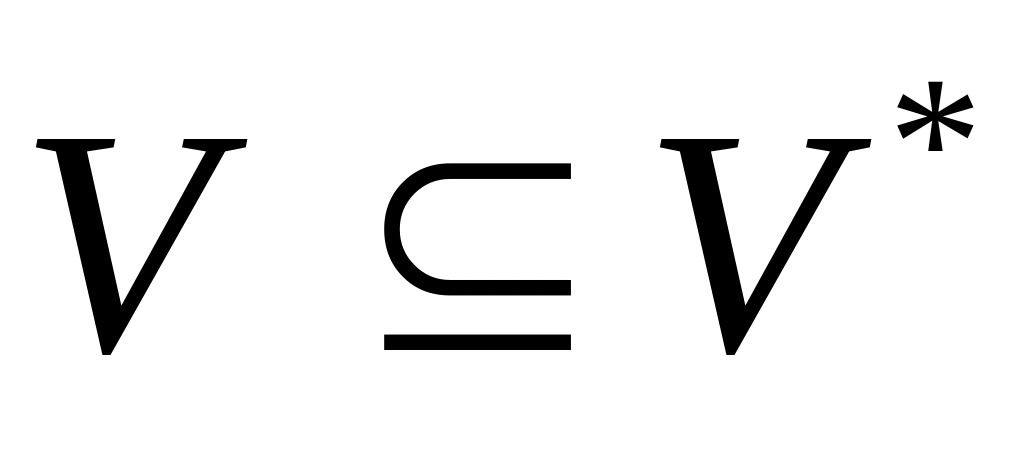 (если ‘да’ , то V
выводима из U)
(если ‘да’ , то V
выводима из U)
Пример
![]()
Проверим,
выводима ли
![]() .
.
Рисуем граф:

 J
J
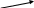
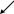
 AB E G
AB E G
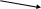 I
I
H
Вывод:
замыкание АВ содержит весь перечень
формул, то есть
![]() ,
JH
– подмножество этой формулы
,
JH
– подмножество этой формулы
![]() выводимо.
выводимо.
Оценка сложности и построение максимального множества
Исходное
множество
![]() разрастается путем добавления новых
элементов.
разрастается путем добавления новых
элементов.
Наихудший
случай: ![]()
![]() -
строится за n
шагов
-
строится за n
шагов
![]() .
.
