1. Расчет на прочность и жесткость при растяжении- сжатии.
1.1. Выбор материала и допускаемых напряжений.
1.1.1. Расчет физико-механических характеристик материала.
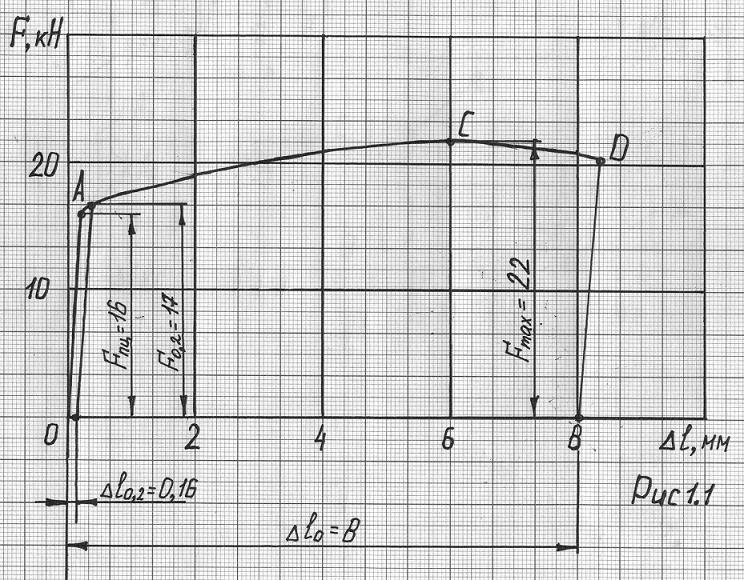
Диаграмма растяжения дюралюминия Д16 изображена на рис 1.1. Образец длиной l0=80 мм и диаметром d0=8 мм разрушается с образованием шейки d1=5,9 мм, что свидетельствует о том, что материал пластичный. Площадь поперечного сечения образца до испытаний:
после разрушения:
относительное остаточное
удлинение:
Относительное остаточное
сужение:
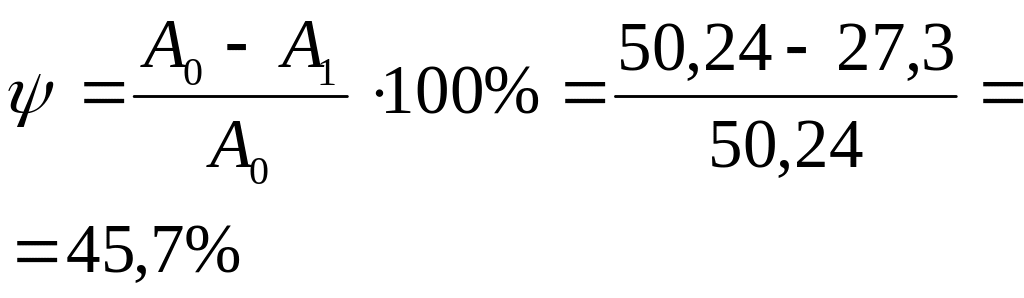
Определим основные характеристики прочности.
Предел пропорциональности
Условный предел текучести
Предел прочности (временное сопротивление σв)
1.1.2. Расчет допускаемых напряжений
Допускаемое напряжение [σ] выбираем, как некоторую долю предельного напряжения σпред, то есть
где n – коэффициент запаса прочности.
Рекомендуемые знания n = 1,5 ÷ 2,5. Примем n = 1,5, тогда
МПа
3
1.2. Проектировочный расчет на прочность ступенчатого стержня.
Для ступенчатого стержня представленного на рис 1.2 необходимо построить эпюру продольных сил, построить эпюру напряжений, отнесенную к площади А0, найти А0 из условия прочности.
1.2.1. Построение эпюры продольных сил.
Составим уравнение равновесия системы (рис 1.2)
,
откуда
Разобьем стержень на 3 участка АВ, ВС, СD, проведем на каждом из них произвольные сечения с координатами z1, z2, z3.
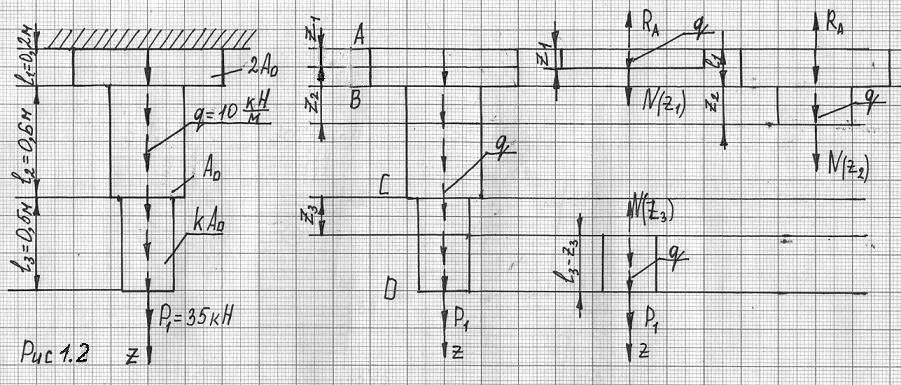
Участок АВ ( 0 ≤ z1 ≤ l1 = 0,2 м ). Из равновесия оставленной верхней части следует, что N(z1) = RA – qz1.
Значение N(z1) в начале участка т.А и в конце участка т.В равна N(z1=0) = RA = 48 кН и N(z1=l1) = RA – ql1 = 48 – 10 ∙ 0,2 = 46 кН.
На участке ВС ( 0 ≤ z2 ≤ l2 = 0,6 м ). Из условия равновесия получим N(z1) = RA – q(l1 + z2).
Значение N(z2) в начале участка т.В и в конце участка т.С равна N(z2=0) = =RA – ql1 = 48 – 10 ∙ 0,2 = 46 кН и N(z2=l2) = RA – q(l1 + l2) = 48 – 10(0,2 + 0,6) = =48 – 8 = 40 кН.
На участке СD ( 0 ≤ z3 ≤ l3 = 0,5 м ). Отбросим верхнюю часть, ее действие заменим продольной силой N(z3). Из условия равновесия следует
N(z3) = Р1 + q(l3 – z3).
Функция N(z3) представляет линейную зависимость. Значение N(z3) в начале участка т.D и в конце участка т.С равна N(z3=l3) = Р1 = 35 кН и N(z3=0) = Р1 + ql3 = 35 + 10 ∙ 0,5 = 35 + 5 = 40 кН.
По полученным данным построим ЭN (рис 1.3, а)
1.2.2. Построение эпюры напряжений.
Нормальное напряжение σ(z) распределяются равномерно по сечению
Где N(z) – продольная сила, А(z) – площадь поперечного сечения.
4
Для определения опасного сечения стержня, в котором возникает максималь-ное напряжение, определим напряжение в долях 1/A0. На участке АВ ( 0 ≤ z1 ≤ l1 = 0,2 м ) нормальные напряжения
Участок ВС ( 0 ≤ z2 ≤ l2 = 0,6 м ).
Участок
CD
( 0
≤ z3
≤ l3
= 0,5 м ).
По полученным данным построим Эσ А0 (рис 1.3, б)