- •2 Способы подбора эмпирических формул
- •2.1 Распространенность степенных и показательных функций среди эмпирических формул
- •2.2 Определение коэффициентов, входящих в эмпирическую формулу
- •2.3 Методы нахождения эмпирических формул для трех переменных
- •2.4 Выявление вида критериального уравнения
- •2.5 Использование программ для Windows при определении вида эмпирического уравнения
- •Список рекомендуемой литературы
2 Способы подбора эмпирических формул
При проведении
эксперимента с целью определения
закономерности
![]() полученные результаты наблюдений
следует оформить в виде таблицы
соответственных значений
полученные результаты наблюдений
следует оформить в виде таблицы
соответственных значений
![]() и
и![]() .
По этим значениям можно построить
кривую зависимости y
от x.
Ее можно приближенно представить
эмпирической формулой
.
По этим значениям можно построить
кривую зависимости y
от x.
Ее можно приближенно представить
эмпирической формулой
![]() .
Выбранная формула должна удовлетворять
условию наилучшего приближения
.
Выбранная формула должна удовлетворять
условию наилучшего приближения
![]() к
к
![]() ,
в некотором интервале значений
,
в некотором интервале значений
![]() .
.
Функцию
![]() можно выразить различными эмпирическими
формулами. Наиболее соответствующую
реальности функцию выбирают определенными
способами. Например, если для выбранной
функции в заданном интервале
можно выразить различными эмпирическими
формулами. Наиболее соответствующую
реальности функцию выбирают определенными
способами. Например, если для выбранной
функции в заданном интервале
![]() наибольшее значение величины
наибольшее значение величины
![]() будет меньше, чем при выборе любой другой
эмпирической формулы. Самый же удачный
способ – метод наименьших квадратов,
по которому функцией, дающей лучшее
приближение, считается такая функция,
для которой величина
будет меньше, чем при выборе любой другой
эмпирической формулы. Самый же удачный
способ – метод наименьших квадратов,
по которому функцией, дающей лучшее
приближение, считается такая функция,
для которой величина
![]() (2.1)
(2.1)
имеет
наименьшее значение. Так как обычно
известны значения функции лишь для
отдельных значений
![]() в заданном интервале, то искомую
эмпирическую формулу
в заданном интервале, то искомую
эмпирическую формулу
![]() подчиняют требованию
сумма
подчиняют требованию
сумма
![]() (2.2)
(2.2)
должна иметь наименьшее значение из всех возможных.
2.1 Распространенность степенных и показательных функций среди эмпирических формул
Это наиболее подходящие для описания любого изучаемого явления функции. Многочлен степени n имеет следующий вид
![]() (2.3)
(2.3)
Частный случай этого выражения
![]() (2.4)
(2.4)
При n=1 многочлен
![]() или
или
![]() (2.5)
(2.5)
геометрически изображается прямой линией.
При n1 (целое число) уравнение (4) представляет кривую параболического типаее вершина находится в точке (l, k). Частными формами этого уравнения являются
![]()
![]() (2.6)
(2.6)
При n0 уравнение (4) представляет кривую гиперболического типа. Частные случаи
![]()
![]()
![]() (2.7)
(2.7)
![]() или
или
![]() .
(2.8)
.
(2.8)
Функциональная зависимость, характеризующаяся дифференциальным уравнением
![]() (2.9)
(2.9)
изображается показательной функцией вида
![]() или
или
![]() (2.10)
(2.10)
Такие функции наиболее часто встречаются в химической практике.
В более сложных случаях иногда удобно представить эмпирическую зависимость в виде
![]() (2.11)
(2.11)
Если
эмпирическую функцию
![]() взять в виде многочлена степени n
взять в виде многочлена степени n
![]() ,
,
![]() (2.12)
(2.12)
то,
увеличивая степень этого многочлена,
можно добиться любой степени приближения
и даже полного совпадения между опытными
данными и формулой. При наличии (n+1)
пар соответственных значений
![]() и
функции
и
функции
![]() ,
то всегда можно подобрать
в форме такого многочлена n-й
степени, чтобы он принимал заданные
значения
,
то всегда можно подобрать
в форме такого многочлена n-й
степени, чтобы он принимал заданные
значения
![]() при заданных значениях аргумента
при заданных значениях аргумента
![]() .
Для этого нужно решить систему (n+1)
уравнений
.
Для этого нужно решить систему (n+1)
уравнений
![]() с (n+1)
неизвестными и получить коэффициенты
с (n+1)
неизвестными и получить коэффициенты
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Тем не менее, нередко, когда эмпирическая формула весьма точно выражает зависимость между заданными численными значениями величин, но типичный график этой формулы не похож на экспериментальную кривую вследствие построения экспериментальной кривой и графика формулы для разных промежутков изменения аргумента. Влияют также численные значения коэффициентов, выбор масштаба координатных осей.
Поэтому удобнее всего использовать метод выравнивания для подбора эмпирической формулы. А затем уже искать значения постоянных коэффициентов, которые дадут наилучшее приближение опытных и вычисленных величин.
Метод
выравнивания заключается в преобразовании
функции
в
линейную зависимость. Получают ее при
замене переменных
и
новыми переменными
![]() и
и
![]() ,
которые должны удовлетворять уравнению
прямой линии
,
которые должны удовлетворять уравнению
прямой линии
![]() .
(2.13)
.
(2.13)
По
экспериментальным значениям
![]() и
и
![]() вычисляют
вычисляют
![]() и
и
![]() ,
наносят на диаграмму с прямоугольными
координатами
,
наносят на диаграмму с прямоугольными
координатами
![]() .
В случае, если точки располагаются
вблизи прямой линии, то выбранная
эмпирическая формула
.
В случае, если точки располагаются
вблизи прямой линии, то выбранная
эмпирическая формула
![]() подходит для характеристики зависимости
подходит для характеристики зависимости
![]() .
.
Пример
4.
Определить порядок химической реакции
по экспериментально полученным данным
по изучению скорости химической реакции
(![]() -время
от начала опыта
-
количество вещества в реакционной смеси
к моменту
),
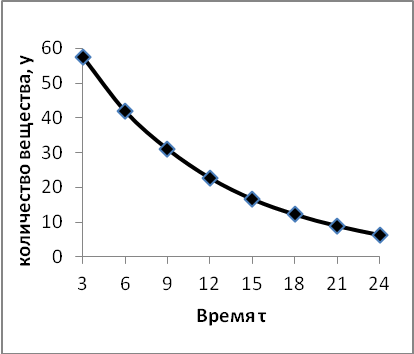
которые приведены в таблице 1 и изображены
на рисунке 1.
-время
от начала опыта
-
количество вещества в реакционной смеси
к моменту
),
которые приведены в таблице 1 и изображены
на рисунке 1.
Таблица 1 – Результаты по изучению скорости химической реакции
|
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
57.6 |
41.9 |
31.0 |
22.7 |
16.6 |
12.2 |
8.9 |
6.5 |
|
4.0535 |
3.7353 |
3.4340 |
3.1224 |
2.8094 |
2.5014 |
2.1861 |
1.8718 |
Предположим, что реакция мономолекулярная, то есть справедлива зависимость
![]() .
(2.14)
.
(2.14)
Выравниванием логарифмированием
![]() .
(2.15)
.
(2.15)
Вычисляем
значения
![]() и
наносим на диаграмму точки в координатах
(
,
и
наносим на диаграмму точки в координатах
(
,
![]() ).
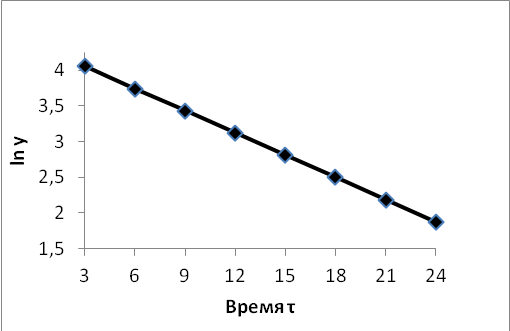
Эти точки (рисунок 2) довольно хорошо
укладываются на прямую линию, что
доказывает применимость формулы
).
Эти точки (рисунок 2) довольно хорошо
укладываются на прямую линию, что
доказывает применимость формулы
![]() и мономолекулярный характер реакции.
и мономолекулярный характер реакции.
|
|
Рисунок 1. Экспериментальная зависимость |
Рисунок 2. Выравнивание экспериментальной зависимости |