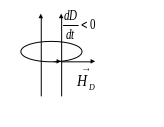- •3. Магнитостатика
- •3.1. Постоянное магнитное поле в вакууме лекции 8-9. Постоянное магнитное поле в вакууме
- •3.1.1. Опыты Ампера и Эрстеда
- •3.1.2. Магнитное поле токов. Вектор магнитной индукции . Силовые линии магнитного поля
- •3.1.3. Закон Био-Савара-Лапласа. Расчет индукции магнитных полей, создаваемых различными токами
- •3.1.3.1. Закон Био-Савара-Лапласа
- •3.1.3.2. Расчет индукции магнитных полей, создаваемых различными токами
- •Б) Поле бесконечно длинного проводника с током (рис.155)
- •В) Магнитное поле в центре кругового тока
- •Сила Ампера. Сила Лоренца. Движение заряженных частиц в магнитном и электрическом поле
- •Сила Ампера
- •3.1.4.2. Сила Лоренца
- •3.1.4.3. Движение заряженных частиц в магнитном и электрическом полях
- •3.1.5. Эффект Холла. Циклотрон. Магнетрон
- •3.1.5.1. Эффект Холла
- •3.1.5.2. Циклотрон
- •Магнетрон
- •3.1.6. Магнитный поток . Работа проводника с током в однородном магнитном поле
- •3.1.6.1. Магнитный поток
- •3.1.6.2. Работа проводника с током в однородном магнитном поле
- •3.1.7. Циркуляция вектора магнитной индукции (Закон полного тока). Поле тороида
- •3.1.7.1. Циркуляция вектора магнитной индукции
- •3.1.7.2. Поле тороида
- •3.1.8. Магнитный момент тока. Контур с током в магнитном поле
- •3.1.8.1. Магнитный момент тока
- •Контур с током в магнитном поле
- •Магнитное поле в веществе
- •3.2.1. Намагничивание вещества. Элементарная теория Ампера намагничивания вещества. Намагниченность магнетика
- •3.2.2. Напряженность магнитного поля. Циркуляция вектора (закон полного тока). Магнитная проницаемость
- •3.2.3. Граничные условия на границе двух магнетиков
- •3.2.4. Магнитное поле разомкнутой магнитной цепи
- •3.2.5. Расчет индукции магнитного поля в веществе. Поле бесконечно длинного проводника с током
- •3.14. Виды магнетиков и их свойства
- •3.14.1. Диамагнетики
- •3.14.2. Парамагнетики
- •3.14.3. Ферромагнетитки
- •3.15. Элементарная теория диа- и парамагнетизма
- •3.15.1. Теория диамагнетизма
- •3.15.2. Теория парамагнетизма
- •3.16. Гиромагнитное соотношение. Опыты Эйнштейна-де-Гааза и Барнетта
- •3.16.1. Гиромагнитное соотношение
- •3.16.2. Опыты Барнетта и Эйнштейна-де-Гааза
- •3.16.2.1. Опыты Барнетта
- •3.16.2.2. Опыт Эйнштейна-де-Гааза
- •3.17. Элементарная теория ферромагнетизма
- •3.18. Кривая намагничивания ферромагнетиков
- •3.2.11. Полная потеря энергии при перемагничивании ферромагнетика
- •3.2.12. Применение магнитных материалов
- •3.2.12.1. Применение магнитотвердых материалов
- •3.2.12.2. Применение магнитомягких материалов
- •4. Электромагнитные явления
- •Опыты Фарадея. Явления электромагнитной индукции
- •Закон электромагнитной индукции (з.Фарадея-Максвелла). Правила Ленца
- •4.2.1. Закон электромагнитной индукции
- •4.2.2. Правило Ленца
- •Вывод закона электромагнитной индукции (Фарадея-Максвелла)
- •Явление самоиндукции. Индуктивность
- •4.5. Токи при замыкании и размыкании электрической цепи
- •Взаимная индукция
- •4.7. Токи Фуко (вихревые) и их применение
- •4.8. Энергия магнитного поля. Энергия перемагничивания ферромагнетика
- •4.8.1.Энергия магнитного поля
- •Энергия при перемагничивании ферромагнетика
- •4.9. Вихревое электрическое поле. Первое уравнение Максвелла
- •4.10. Токи смещения. Второе уравнение Максвелла
- •4.11. Полная система уравнений Максвелла в интегральной форме
4.9. Вихревое электрическое поле. Первое уравнение Максвелла
Из п.4.2 лекций 12-14
следует, существуют несколько типов
изменения магнитного потока. Один из
них – это за счет изменения магнитного
поля во времени (![]() ).
Пусть в изменяющемся во времени магнитном
поле находится неподвижный проводящий
контур. Опыт показывает, что в нем
возникает индукционный ток. Порождение
индукционного тока в контуре свидетельствует
о том, что изменение магнитного поля во
времени вызывает появление в контуре
сторонних сил, действующих на носители
тока. В связи с этим возникает вопрос.
Какова природа этих сил? Отметим, что
эти силы не связаны ни с химическими,
ни с тепловыми процессами в контуре,
т.к. они не протекают.
).
Пусть в изменяющемся во времени магнитном
поле находится неподвижный проводящий
контур. Опыт показывает, что в нем
возникает индукционный ток. Порождение
индукционного тока в контуре свидетельствует
о том, что изменение магнитного поля во
времени вызывает появление в контуре
сторонних сил, действующих на носители
тока. В связи с этим возникает вопрос.
Какова природа этих сил? Отметим, что
эти силы не связаны ни с химическими,
ни с тепловыми процессами в контуре,
т.к. они не протекают.
Максвелл на
поставленный вопрос ответил следующим
положением: «Изменяющееся
во времени магнитное поле порождает в
пространстве вихревое электрическое
поле![]() ,
независимо от того, существует ли в
пространстве проволочный контур или
нет».
Наличие контура лишь позволяет обнаружить
существование в нем индукционного тока
(см формулу 622).
,
независимо от того, существует ли в
пространстве проволочный контур или
нет».
Наличие контура лишь позволяет обнаружить
существование в нем индукционного тока
(см формулу 622).
Вихревое электрическое поле существенно отличается от электрического поля, порождаемого электрическими зарядами.
Во-первых, силовые линии вихревого электрического поля замкнутые, а электрического поля зарядов не замкнутые (см. Лекцию 1).
Во-вторых,
циркуляция вектора напряженности
вихревого поля
не
равна нулю, т.е.![]() ,
а электрического поля зарядов
,
а электрического поля зарядов
![]() равна нулю, т.е.
равна нулю, т.е.
![]() .
.
Максвелл на основании предположения написал уравнение, описывающее вихревое электрическое поле.
По закону
электромагнитной индукции, ЭДС индукции,
возникающая в контуре за счет изменения
магнитного поля во времени, равна
![]() .
.
С другой стороны,
по Максвеллу![]() ,
откуда одно из уравнений Максвелла
записывается в виде
,
откуда одно из уравнений Максвелла
записывается в виде
|
(622) |
||
|
|
||
|
|
||
|
рис.266 |
В общем случае, если электрическое поле создано электрическими зарядами и изменяющимся во времени магнитном поле , то циркуляция результирующего поля
![]()
равна:
![]() (623)
(623)
т.к.![]() .
.
Выражение (623) – одно из уравнений Максвелла.
4.10. Токи смещения. Второе уравнение Максвелла
Известно, что постоянный ток создает вокруг себя постоянное магнитное поле, уравнение которого имеет вид
|
(624) |
Уравнение непрерывности для постоянного тока равно
|
(625)
|
Возникает вопрос: справедливо ли уравнение (624) для переменных магнитных полей, порождающих переменными токами? Известно, что для переменных токов уравнение непрерывности описывается формулой
|
(626) |
На этот вопрос Максвелл ответил следующим образом. Для того, чтобы уравнения (624) и (626) описывали переменные магнитные поля, необходимо в правую часть уравнения (624) дополнить одно слагаемое, имеющее размерность силы тока, которое Максвелл называл током смещения Iсм. Тогда уравнение (624) запишется в виде
|
(627) |
Токи смещения возникают при изменении электрического поля во времени
|
(628) |
С учетом (628) уравнение (627) запишется в виде
|
(629) |
Формула (629) есть второе уравнение Максвелла и называется законом полного тока.
Смысл уравнения
(629). Вихревое
магнитное поле создается не только
током проводимости
![]() ,
но и изменяющимся во времени электрическим
полем
,
но и изменяющимся во времени электрическим
полем
![]() .
.
Токи смещения существенно отличаются от токов проводимости.
Во-первых, токи проводимости создаются движением электрических зарядов, а токи смещения – изменяющимся во времени электрическим полем.
Во-вторых, при прохождении токов проводимости в проводнике выделяется джоулево тепло, а токи смещения не выделяют тепла.
В-третьих, токи смещения возникают всюду, даже в вакууме, если существует изменяющееся во времени электрическое поле.
Направление магнитного поля, воздаваемое токами смещения определяется по правилу буравчика (рис.267).
|
рис.267 |