3.16.2.2. Опыт Эйнштейна-де-Гааза

Идея опыта следующая. Тонкий железный стержень (обр) подвешивался на

Рис.229

упругой нити с известным модулем сдвига (G) и помещался внутрь соленоида (с) (рис.229). Под действием поля соленоида стержень намагничивается и возникает механический момент импульса, вектор которого направлен противоположно вектору намагниченности. В результате стержень поворачивается вокруг оси, проходящей через ось соленоида. Поворот стержня фиксируется закручиванием нити (н) с зеркальцем с помощью луча (л), падающего на зеркальце (з). При изменении направления намагниченности стержень поворачивался в противоположную сторону. Таким образом, можно было определить угловую скорость, которая очень мала. Чтобы усилить эффект к соленоиду подключился переменный ток с частотой , которая равна частоте механических колебаний стержня при .

Момент сил, действующий на упругую нить, пропорционален углу поворота нити (зеркальце) , т.е. , а момент импульса M, т.е. . Намагниченность пропорциональна H, т.е. JH.

Тогда можно найти соотношение . В опыте Эйнштейна-де-Гааза , т.е. - это есть спиновое гиромагнитное соотношение. Таким образом доказана спиновая природа ферромагнетизма, т.е. намагниченность ферромагнетиков обусловлена ориентацией спиновых магнитных моментов электронов.

3.17. Элементарная теория ферромагнетизма

Первая теория ферромагнетизма была создана Розингом (1892 г.) и Вейссом (1907 г.) на основе гипотезы о том, что в ферромагнетике действует внутримолекулярное поле, напряженность которого определяется формулой

, (546)

где - постоянная внутримолекулярного поля, - намагниченность насыщения.

Это поле обуславливает спонтанную (самопроизвольную) намагниченность в ферромагнетике. На основании этой теории можно качественно объяснить существование температуры Кюри . Однако долгое время оставалось неясной природа внутримолекулярного поля. После появления квантовой механики в 1928 г. Я.Френкель, независимо от него В.Гейзенберг высказали предположение, что в

Рис.230	Рис.231

ферромагнетиках существуют обменные взаимодействия, которые и приводят к определенной ориентации спиновых магнитных моментов (спинов). На примере можно объяснить обменные взаимодействия.

Рассмотрим молекулу водорода. Пусть первоначально два атома находятся на большом расстоянии друг от друга ( , где d – диаметр атома) (рис.230).

Тогда вероятность перехода электрона (1е) первого атома на второй практически равна нулю. Поэтому атомы не обменивают электронами. Сблизим атомы

до характерного расстояния , при котором электронные орбиты атомов перекрываются. В этом случае вероятность перехода электронов из одного атома на другой и обратно велика, т.е. атомы обмениваются между собой электронами (рис.231). На рис.231 показано нахождение электрона (2е) второго атома на орбите первого атома и электрона (1е) первого атома на орбите второго атома. Такие переходы обусловлены обменными взаимодействиями, энергия которых определяется формулой

, (547)

где - обменный интеграл, имеющий сложное выражение,

- сумма спинов электронов (для многоэлектронного атома).

Расчеты показывают, что при >0, т.е. обменная энергия отрицательна , то спиновые моменты ориентируются параллельно ( ), соответственно магнетики являются ферромагнетиками (например, Fe, Ni, Co). Если <0, т.е. , то возникает антипараллельная ориентация ( ), присущая для антиферромагнетиков, например, марганец Mn.

Опыты и теория показывают, что не во всех магнетиках возникают обменные взаимодействия, а только у тех, у которых имеются недостроенные электронами оболочки. Таковыми являются 3d-переходные и f-редкоземельные металлы. В этих металлах у атомов имеются не полностью занятые электронами оболочки. Например, для железа Fe электронное состояние записывается формулой , где 1, 2, 3, 4 – главное квантовое число (n=1, 2, 3, …, ), s, p, d – уровни (состояние электронов оболочки), характеризуемые орбитальным квантовым числом (l =0, 1, 2,…). Верхние цифры показывают число электронов на каждом уровне. d - оболочка максимально должна заполняться 10 электронами. Однако в случае Fe и переходных элементов d - оболочки заполняются электронами частично (в случае Fe всего 6 электронов вместо восьми), а часть электронов переходят выше стоящие оболочки (для железа два электрона перешли на 4s - оболочки). Такая картина наблюдается и для редкоземельных металлов, где f - оболочка не полностью заполнена электронами. Существуют критерии ферромагнетизма, т.е. для параллельной ориентации спинов необходимы условия:

1. В атоме должны быть недостроенные электронами оболочки;

2. Обменный интеграл должен быть положительным >0;

   Рис. 232	Рис. 233

3. Должно выполняться 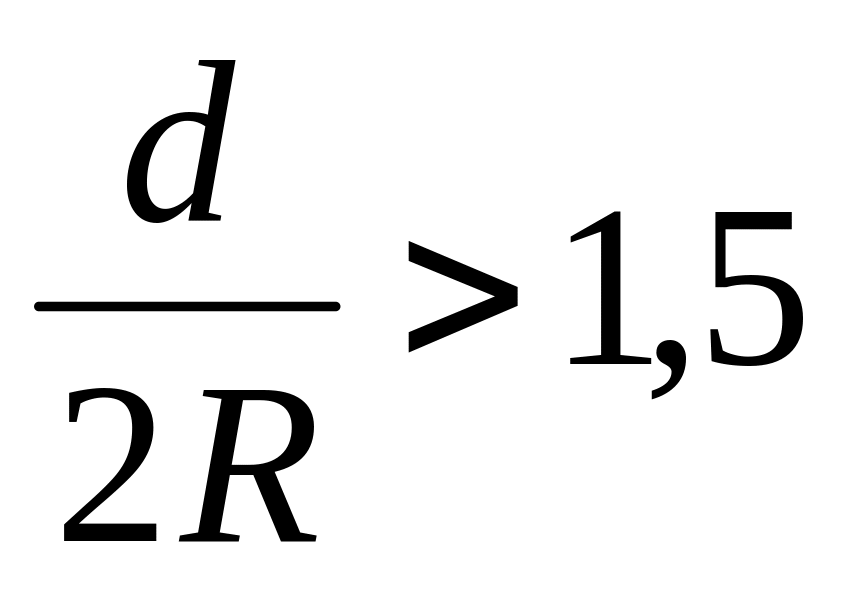, где R – радиус недостроенной орбиты, d – параметр решетки.

Теория показывает, что при минимуме полной энергии ферромагнетик разбивается на большое число магнитных доменов.

Магнитный домен – это микрообласть с размерами порядка 10^-4  10^-3 см, которая спонтанно (самопроизвольно) намагничена, т.е. внутри домена спиновые моменты ориентированы параллельно (рис.233). Первая теория магнитного домена была создана Ландау и Лифшицем в 1935 году и рассчитали размер домена.

Между доменами существуют доменные границы, которые имеют различные формы (рис.232-234): 180-градусные, 90-градусные, 65-градусные и цилиндрические магнитные домены (рис.233 и 234).

Рис. 234.

На рис.233 стрелками показаны спонтанная намагниченность доменов, а на рис.234 - показан вектор намагниченности цилиндрического домена, направленный перпендикулярно плоскости чертежа от нас.

Экспериментально магнитные домены и доменные границы наблюдали Биттнер, Акулов, Дорфман, Блох, Неель и другие. Теорию динамики доменных границ создали Блох, Неель, Ландау и другие.

Полная энергия ферромагнетика определяется формулой

, (548)

Рис.235

где - обменная энергия, - энергия магнитной анизотропии, - константа магнитной анизотропии, - направляющие косинусы, т.е. - угол между вектором намагниченности и кристаллографическими осями.

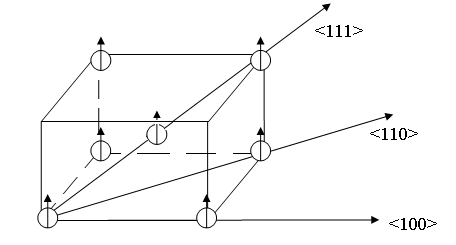
Существуют кристаллографические оси легкого и трудного намагничивания. Например, для железа (рис.235, 236) кристаллическая решетка является объемно центрированной (рис.235).

Тогда ось <100> является осью легкого намагничивания (кривая 1 на рис.236), а <111> - называется осью трудного намагничивания (кривая 3 на рис.236). Разница между энергиями трудного и легкого намагничивания называется энергией магнитной анизотропии и вид кривой намагничивания зависит от кристаллографических осей (рис.236).

Рис.236

- магнитоупругая энергия,

где - магнитострикционная деформация, т.е. деформация кристаллической решетки, обусловленная поворотом вектора намагниченности под действием внешнего магнитного поля. При магнитострикции изменяются продольные и поперечные размеры ферромагнетика, т.е. ;

- упругое механическое напряжение;

- элементарный объем.

- энергия размагничивающего поля, где - напряженность размагничивающего поля, N – размагничивающий фактор, зависящий от формы образца ферромагнетика, J - намагниченность.

- магнитная постоянная. При минимуме полной энергии W ферромагнетику выгодно разбиться на магнитные домены.