МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИНЖЕНЕРНЫХ ТЕХНОЛОГИЙ

Кафедра информационных и управляющих систем

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям

по курсу

" Диагностика и надежность систем

автоматизации"

для бакалавров направления

220700_- Автоматизация технологических процессов и производств________

Ю. П. Барметов

ВОРОНЕЖ 2011

1. Расчет показателей надежности объектов по известному закону распределения вероятности безотказной работы

Расчет показателей надежности объектов при известном законе распределения вероятности безотказной работы или времени наработки до отказа заключается в подстановке численных значений параметров распределения в формулы, приведенные в лекционном курсе, и вычислении заданных показателей надежности.

Пример 1.

При расчете показателей для нормального распределения времени наработки до отказа и распределения Вейбулла желательно использовать систему Mathcad, что позволит достаточно легко вычислять интеграл вероятности отказов , находить значения гамма-функции путем обращения к встроенной функции Г(x) (символ Г из греческого алфавита) и т.д.

Пример 2.

II. Расчет показателей надежности систем без резервирования

В системах без резервирования отказ любого элемента приводит к отказу всей системы, поэтому вероятность безотказной работы системы равна произведению вероятностей безотказной работы всех элементов. При экспоненциальном законе распределения вероятности безотказной работы получаем простое выражение для вероятности безотказной работы системы: . Среднее время наработки системы до отказа равно .

Пример 3.

III. Расчет показателей надежности систем с резервированием отдельных элементов или групп элементов.

Для расчета необходимо:

- составить структурную схему системы;

- разделить условно схему на участки содержащие только нерезервированные элементы, отдельные резервированные элементы с целочисленной кратностью резервирования, группы резервированных элементов с дробной кратностью резервирования и мажоритарным резервированием;

- для каждого участка определить вероятность его безотказной работы с учетом вида резервирования;

- перемножая вероятности безотказной работы для последовательно соединенных участков или вероятности отказов для параллельно соединенных участков, записать выражение для вероятности безотказной работы системы;

- используя формулы для выражения показателей надежности через вероятность безотказной работы системы, получить заданные в контрольной работе показатели.

Вероятность безотказной работы резервированных элементов и групп получают рассмотренными в лекциях методами.

1. При резервировании одного элемента несколькими резервными с нагруженным резервом (поэлементное резервирование) перемножают вероятности отказов всех элементов, а вероятность безотказной работы такой группы определяют как

, где - вероятность безотказной работы i-го элемента.

Для двух элементов (дублированного элемента) ;

2 . Для резервированной группы с дробной кратностью резервирования (скользящее резервирование) или с мажоритарным резервированием при нагруженном резерве вероятность безотказной работы получают методом перебора состояний. Так для двух основных и одного резервного элемента

.

Пример 4.

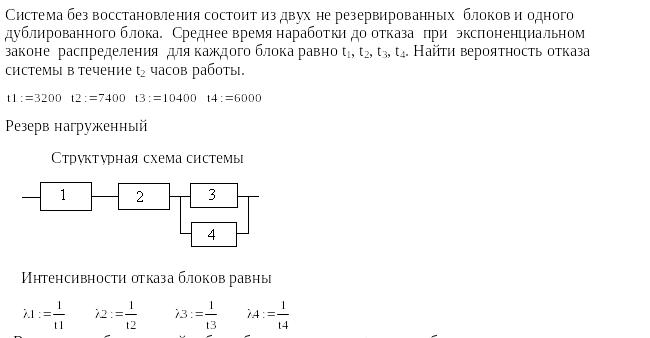
3. При резервировании одного элемента несколькими резервными с ненагруженным резервом и одинаковыми постоянными интенсивностями отказов всех элементов λ вероятность безотказной работы группы получают используя распределение Пуассона

, n – количество резервных элементов, i!=1 при i=0.

4. При резервировании одного элемента несколькими резервными с ненагруженным резервом и различными постоянными интенсивностями отказов всех элементов λ_i вероятность безотказной работы группы получают через свертку плотностей вероятностей отказа элементов.

Для двух элементов .

Для трех .

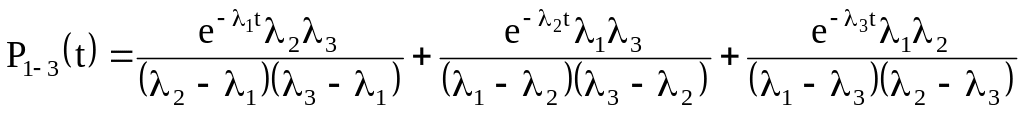5. При ненагруженном резервировании группы элементов с различной интенсивностью отказов вероятность безотказной работы группы находится путем решения системы дифференциальных уравнений, составленных по графу состояний группы (см. лекции).

Пример 5. Найти среднее время наработки до отказа невосстанавливаемой системы управления, содержащей дублированный контроллер с ненагруженным резервом и интенсивностью отказов каждого контроллера , три датчика температуры с интенсивностями отказов , образующих мажоритарно резервированную группу, два датчика давления с интенсивностями отказов и два исполнительных механизма с .

Структурная схема системы:

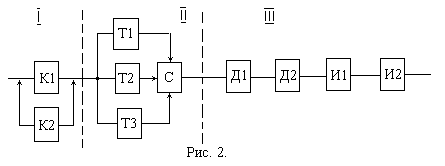
Разделим условно схему на три участка: первый содержит резервированный контроллер, второй – резервированный датчик температуры, третий – нерезервированные элементы.

Вероятность безотказной работы первого участка при одинаковых интенсивностях отказов обоих элементов и ненагруженном резерве в соответствии с распределением Пуассона определяется как .

Вероятность безотказной работы второго участка при одинаковых интенсивностях отказов всех элементов и нагруженном резерве (элемент сравнения С введен формально, чтобы показать, что это мажоритарный резерв; сравнение выходов датчиков температуры и принятие решения выполняет контроллер) находится методом перебора состояний:

Поскольку все интенсивности отказов элементов постоянны, распределение вероятности безотказной работы элементов подчиняется экспоненциальному закону и

Для третьей группы

Вероятность безотказной работы системы

.

Раскрывая скобки, получим

.

Обозначая и , перепишем выражение для вероятности безотказной работы системы: .

Среднее время наработки системы до отказа определяется как .

Интеграл вида интегрируем по частям и он, с учетом обозначений , равен .

Тогда .

IV. Расчет показателей надежности резервированных систем.

А.Также как и для невосстанавливаемых систем вначале необходимо составить структурную схему системы и условно разделить на отдельные группы элементов с резервированием и элементов нерезервированных. Если интенсивность восстановления элементов нерезервированной группы одинакова и после отказа системы исправные элементы отключаются, элементы этой группы можно считать одним элементом с интенсивностью восстановления равной интенсивности восстановления одного исходного элемента, и интенсивностью отказов равной сумме интенсивностей отказов всех элементов, входящих в группу.

Б. Следующим наиболее сложным и ответственным этапом является составление графа состояний.

Следует помнить, что при определении вероятности безотказной работы или среднего времени наработки системы до отказа (до первого отказа) граф состояний составляют усеченным, т.е. не содержащим ветвей, выходящих из вершин, соответствующих неработоспособным состояниям. При определении функции готовности, коэффициента готовности, среднего времени наработки на отказ составляется полный граф.

Если количество восстанавливающих бригад не ограничено, составлять графы состояний можно для отдельных групп резервированных или нерезервированных элементов.

При составлении графа необходимо соблюдать принцип ординарности, т.е. переход между вершинами, соединенными общей ветвью (смежными вершинами) происходит в результате отказа или восстановления только одного элемента. Если стоит задача составить граф для системы, в которой после отказа работоспособные элементы отключаются и система включается только после полного восстановления всех элементов, то для соблюдения принципа ординарности вводятся промежуточные вершины, соответствующие нерабочим состояниям в которых система может быть работоспособной, но она не включена.

П ример 6. Для расчета коэффициента готовности составить структурную схему и граф состояний системы, состоящей двух основных и одного резервного элемента, если интенсивности отказа всех элементов различные, а интенсивности восстановления одинаковые. Восстановление ведут 2 бригады. Резерв нагруженный, после отказа системы исправный блок отключается. Включение системы производится после восстановления работоспособного состояния.

1. Граф состояний по этому условию представлен на рис.3.

Построение графа начинают с нулевой вершины, соответствующей всем работоспособным и, в данном примере с нагруженным резервом, работающим элементам. Поскольку отказать может любой работающий элемент и интенсивности отказов у всех элементов различные, а, следовательно, и состояния, полученные в результате отказа разных элементов, будут различными, добавляем три новых вершины для состояний 1, 2 , 3 и три ветви перехода с интенсивнос-тями λ₁, λ₂, λ_3.

В первом состоянии, возникшем в результате отказа первого элемента, работают элементы 2 и 3, которые также могут отказать, а первый элемент может быть восстановлен. В результате восстановления первого элемента система вновь возвратится в нулевое состояние, в результате отказа третьего элемента перейдет в новое, четвертое состояние; в результате отказа второго элемента – в пятое состояние. В четвертом состоянии неработоспособны первый и третий элементы, в пятом – первый и второй. Поскольку число оставшихся работоспособных элементов в этих состояниях меньше количества основных элементов, то эти состояния соответствуют неработоспособной системе и соответствующие им вершины заштрихованы.

Во втором состоянии неработающий второй элемент может быть восстановлен и система возвратится в нулевое состояние; первый элемент может отказать и система перейдет в пятое состояние, введенное ранее; может отказать третий элемент и система перейдет в новое, нерабочее шестое состояние.

Аналогичные переходы возможны из третьего состояния.

В четвертом состоянии неработоспособны первый и третий элементы и работоспособен второй. Так как по условию задачи при отказе системы исправные элементы отключаются и в отключенном состоянии не отказывают, дальнейшего перехода из нерабочего в новое нерабочее состояние не происходит. Если по условию задачи отключение не происходит, граф, как будет показано дальше, продолжает расширяться. Неработоспособные элементы могут быть восстановлены, причем, две бригады могут восстанавливать одновременно два элемента, но окончание восстановления все равно происходит в разные моменты времени, и если раньше будет восстановлен первый элемент, система возвратится в третье состояние, а если третий – в первое состояние.

Продолжая анализ всех состояний поочередно, расставляем вершины и ветви графа. Заканчивают построение когда все введенные вершины будут проанализированы.

2. Если резерв ненагруженный, то при двух восстанавливающих бригадах в графе состояний исчезнет ветвь, выходящая из нулевой вершины в третью, т.к. в нулевом состоянии третий (резервный) элемент отключен и он не отказывает, но тем не менее, третье состояние, соответствующее работающим первому и второму элементам и неработоспособному третьему элементу, возникает в результате восстановлений из шестого и четвертого состояний.

3. Если определяется среднее время наработки системы до первого отказа, то все ветви, выходящие из заштрихованных вершин, соответствующих неработоспособным состояниям, следует удалить.

4. Если восстановление производит одна бригада, то из каждых двух ветвей, выходящих из заштрихованных вершин, следует оставить только одну.

5. Если после отказа системы работоспособные блоки не отключаются и восстановление ведут две бригады, граф имеет вид, показанный на рис.4.

6. Если после отказа системы ее отключают и ведут ремонт до полного восстановления, то получим граф, показанный на рис. 5.

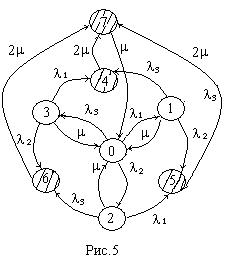
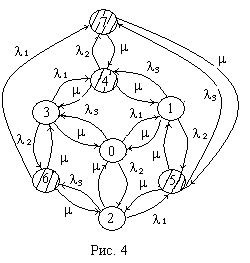
7. Если интенсивности отказа всех элементов одинаковы и равны λ, граф значительно упростится, так как при отказах нет разницы какой из элементов отказал, в результате получаем всего три состояния: работают все, неработоспособен один элемент и неработоспособны два. Интенсивности отказов для каждого состояния равны сумме интенсивностей отказов всех работающих элементов, интенсивность восстановления равна сумме интенсивностей одновременно восстанавливаемых элементов, но это количество не может быть больше числа отказавших элементов и больше числа восстанавливающих бригад.

П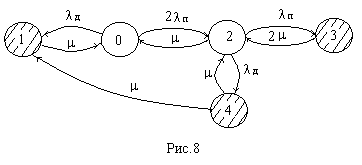 ример 7. Для системы, содержащей преобразователь с нагруженным резервным и пять датчиков температуры, составить полный граф состояний, если интенсивности отказов преобразователей одинаковы и равны λ_п, интенсивности отказов первого и второго датчиков равны λ₁, остальных – λ₂. Интенсивности восстановления (или замены) всех элементов равны μ. Количество восстанавливающих бригад не ограничено, после отказа исправные элементы отключаются.

Объединим все датчики в один блок с интенсивностью отказов равной сумме интенсивностей отказов всех датчиков (все датчики работают одновременно) , и интенсивностью восстановления μ.

Если восстанавливает одна бригада, то граф можно упростить, объединив третью и четвертую вершины, т.к. восстанавливать после отказа системы желательно тот элемент, который позволит вернуть систему в рабочее состояние (см. рис.9). В третьем состоянии могут быть неработоспособными оба преобразователя либо один преобразователь и один датчик.

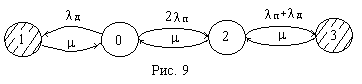
При расчете времени наработки до первого отказа или вероятности безотказной работы усеченный граф не зависит от количества восстанавливающих бригад, т.к. выходы из нерабочих состояний запрещены (см. рис.10)

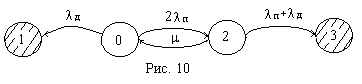
При расчете функции готовности, коэффициента готовности или среднего времени наработки на отказ этой системы в случае неограниченного количества бригад можно разделить систему на резервированный преобразователь и нерезервированные датчики и для этих двух групп составить отдельно графы, которые показаны на рис. 11 а) и рис. 11 б).

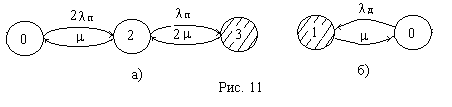
В. По графам состояний записывают системы дифференциальных уравнений. Составление уравнения для выбранной вершины начинают с записи в левой части уравнения производной от вероятности нахождения системы в состоянии, соответствующем выбранной вершине. В правой части со знаком «минус» записывают эту же вероятность, умноженную на сумму интенсивностей всех переходов из выбранной вершины в смежные, и со знаками «плюс» вероятности смежных вершин, умноженные на интенсивности переходов из них в выбранную вершину.

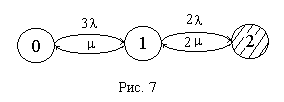
Пример 8. Составить систему уравнений для графа представленного на рис. 8.

,

,

, (1)

,

.

В приведенной системе слагаемые в правых частях уравнений расставлены по возрастанию индексов. Для проверки нужно просуммировать правые части всех уравнений и получить нуль, т.к. каждое слагаемое должно присутствовать в системе дважды и с разными знаками.

При расчете вероятности безотказной работы или среднего времени наработки до первого отказа уравнения составляют только для работоспособных состояний и проверка не выполняется, в остальных случаях – для всех состояний. Так для графа на рис. 10 система уравнений записывается как

. (2)

Г. Расчет коэффициента готовности рассмотрим на примере системы, граф которой представлен на рис.8 и записана система уравнений (1).

Коэффициент готовности определяется как предел функции готовности при . Функция же готовности равна сумме вероятностей рабочих состояний

.

С учетом этого коэффициент готовности будет равен

Предельные значения вероятностей проще всего искать путем перехода в уравнениях системы (1) к пределам при . Поскольку все значения вероятностей стремятся к некоторым постоянным значениям P_i, их производные стремятся к нулю и система (1) принимает вид:

,

,

,

,

.

Полученная система алгебраических уравнений, связывающая предельные значения вероятностей P_i, является недоопределенной т.к. сумма всех левых частей уравнений равна 0, для ее доопределения необходимо любое уравнение заменить суммой вероятностей всех состояний, которая, как известно, равна 1. Заменим самое длинное третье уравнение

,

,

, (3)

,

.

Решать полученную систему относительно Р₀, Р₂ можно последовательно исключая «лишние» неизвестные и уменьшая количество уравнений. Проще воспользоваться возможностями системы Mathcad по выполнению операций с матрицами. Систему (3) в матричном виде можно записать как , где А- матрица, Р и В – векторы. Решением ее будет вектор Р, равный Р=А^-1В. Ниже показано решение в системе Mathcad

Д. Расчет среднего времени наработки на отказ в заданиях рассматривается только при . Это избавляет студентов от необходимости определения функций для вероятностей рабочих состояний, т.е. от необходимости решать систему дифференциальных уравнений.

А при 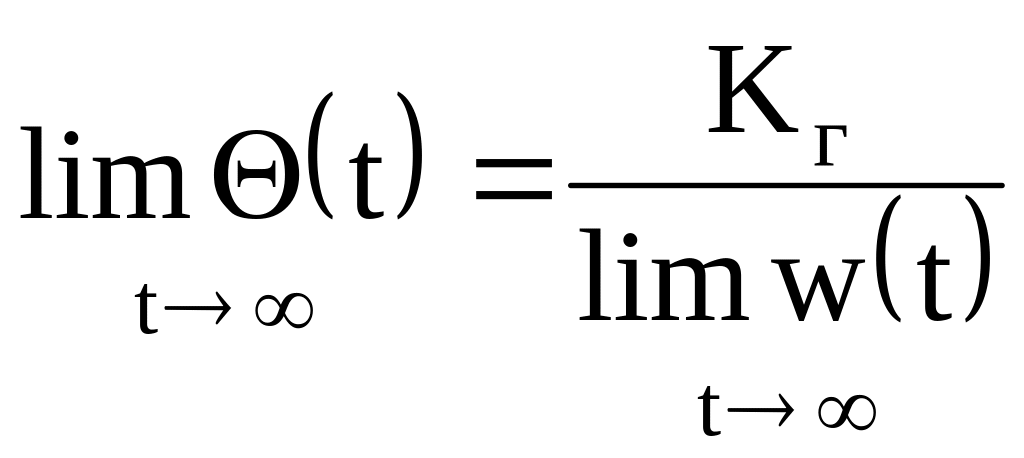, где w(t) – параметр потока отказов, определяемый как сумма вероятностей рабочих состояний, из которых возможен переход в нерабочие, умноженных на интенсивности переходов. При переходе к пределу, вероятности рабочих состояний заменяются их предельными значениями. Для рассмотренного в пункте Г примера .

Е. Среднее время наработки системы до первого отказа определяют по усеченному графу через вероятность безотказной работы системы Рс как . Чтобы не решать систему дифференциальных уравнений и потом не вычислять интеграл, проще перейти в системе дифференциальных уравнений к преобразованиям Лапласа, решить полученную алгебраическую систему относительно изображений вероятностей рабочих состояний, разделить сумму этих изображений на s, что соответствует интегрированию оригинала, а затем воспользоваться правилом предельного перехода .

Выражение для вычисления Тср поучается достаточно простым .

Пример 9. Для системы, граф которой представлен на рис. 10, и описание дано системой уравнений (2), дифференциальные уравнения в преобразования Лапласа имеют вид:

,

, (4)

где , - начальные условия. Считаем, что исходным при включении системы является нулевое состояние, тогда , .

Выражая из второго уравнения системы (4) и подставляя его в первое получим:

,

Подставляем выражение для , находим

.

Подставляя численные значения для интенсивностей и 0 для s, вычисляем значения среднего времени нахождения системы в нулевом и втором состояниях: и . Их сумма и будет средним значением времени наработки до первого отказа.