13. Момент силы

Моментом силы относительно точки называется векторное произведение

.

Моментом 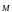нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки.

Момент импульса 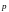МТ относительно точки или полюса . Так называется векторное произведение

.

Их связь

Целесообразность введения моментов импульса и силы оправдывается тем, что они связаны между собой соотношением, которое называется уравнением моментов. Дифференцируя уравнение для момента импульса МТ по времени, получаем . Но при неподвижном начале импульс частицы коллинеарен с ее скоростью . Кроме того, 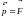. Значит, . Отсюда

.

Это и есть уравнение моментов для одной МТ. Оно справедливо как в ньютоновской, так и в релятивистской механике.

14. Закон сохранения момента импульса

Распространим теперь это уравнение на систему МТ. Для этого напишем его для каждой точки, понимая под момент всех действующих на нее сил, как внутренних, так и внешних. Затем сложим все эти уравнения. При этом моменты внутренних сил исключатся. Силы действия и противодействия для каждой пары МТ направлены противоположно и направлены вдоль одной и той же прямой. Момент таких двух сил, а значит и моменты всех внутренних сил равны нулю. В результате получаем для суммарного момента импульса всех МТ системы

.

15. Работа

Работой силы на перемещении 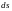выражается формулой (см. рис.):

,

г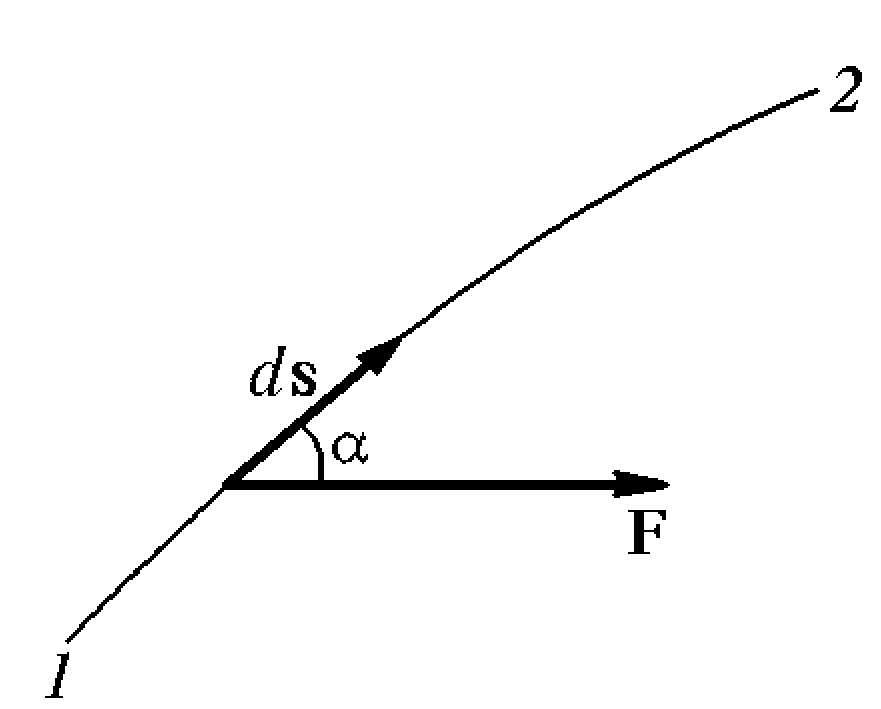 де — угол между векторами и Поскольку перемещение предполагается бесконечно малым, величина называется элементарной работой. Если вспомнить скалярное произведение, элементарная работа может быть записана в виде:

.

Кинетическая энергия

Величина

называется кинетической энергией МТ.

16. Консервативные силы – такие силы, при которых силы взаимодействия зависят только от конфигурации МТ системы (т.е. их координат) и работа этих сил при перемещении системы из произвольного начального положения в произвольное конечное положение не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы.

К консервативным силам относятся гравитационная сила, сила тяжести, упругая сила, сила Кулона и многие другие.

Неконсервативные силы – все силы, которые не являются консервативными.

Потенциальная энергия - работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое.

Примеры потенциальной энергии:

1. Сила тяжести. . Потенциальная энергия равна . Здесь  — высота положения МТ, — произвольная константа. За нулевой уровень можно принять произвольный уровень, например уровень пола, уровень моря и т.д. можно положить равной нулю.

2. Потенциальна энергия растянутой пружины. . Эта сила совершает работу

.

Если упругую энергию пружины в недеформированном состоянии считать равной нулю, то

.

3. Потенциальная энергия гравитационного притяжения двух МТ.

.

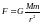Если выбрать потенциальную энергию в бесконечности равной нулю, то

.

Потенциальная энергия отрицательна.

17. Закон сохранения и изменения механической энергии

Допустим теперь, что в системе кроме консервативных сил присутствуют неконсервативные, которые называются еще диссипативными. Тогда работа всех сил может быть разделена на две части: консервативную и диссипативную . Первая часть выражается через разность потенциальных энергий и вся работа выражается через разность кинетических энергий. Тогда

,

или

.

То есть в этом случае полная механическая энергия уменьшается.

Работа диссипативных сил переводит механическую энергию во внутреннюю тел, составляющих систему. На сегодняшний день считается, что если учесть все энергии, а не только механическую, то суммарная энергия сохраняется.

18. Абсолютно неупругий удар - столкновение двух тел, при котором они соединяются вместе и движутся дальше как одно тело.

Примером может служить попадание пули в подвижную мишень.

,

Абсолютно упругий удар - удар двух тел, при котором не меняется внутренние энергии этих тел.

Точно таких ударов, конечно, не существует. Но близко — бильярдные шары.

,

19. Абсолю́тно твёрдое те́ло — второй опорный объект механики наряду с материальной точкой. Механика абсолютно твердого тела полностью сводима к механике материальных точек (с наложенными связями), но имеет собственное содержание (полезные понятия и соотношения, которые могут быть сформулированы в рамках модели абсолютно твердого тела), представляющее большой теоретический и практический интерес.

Вращение вокруг неподвижной оси

П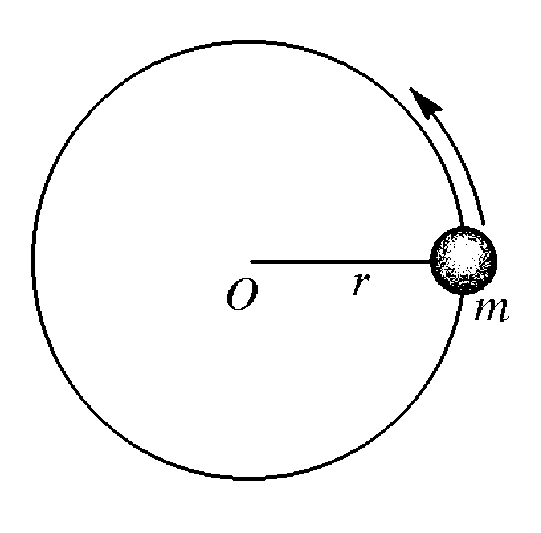 рименим уравнение моментов относительно оси к рассмотрению вращательного движения. За неподвижную ось моментов удобно выбрать ось вращения. Если (см. рисунок) МТ вращается по окружности радиуса , то момент ее импульса относительно оси вращения равен . Пусть — угловая скорость вращения, тогда , и, следовательно, . Если вокруг оси вращается система МТ с одной и той же угловой скоростью , то 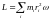, где суммирование производится по всем МТ системы. Величину можно вынести из-под знака суммы. Тогда

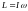
Момент инерции – величина , равная сумме произведений масс МТ на квадраты их расстояний до оси вращения:

.