1.Кинематика материальной точки-раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.

Тело отсчёта-тело, относительно которого рассматривается движение

Равномерным прямолинейным движением называют такое происходящее по прямолинейной траектории движение, при котором тело (материальная точка) за любые равные промежутки времени совершает одинаковые перемещения.

Движение тела в пространстве-изменение положения тела в пространстве с течением времени. Под положением понимается относительное положение, т.е. положение тела относительно других тел.

Декартова система координат-

В качестве пространственной системы отсчета можно взять произвольное твердое тело и связать с ним координатные оси, например, д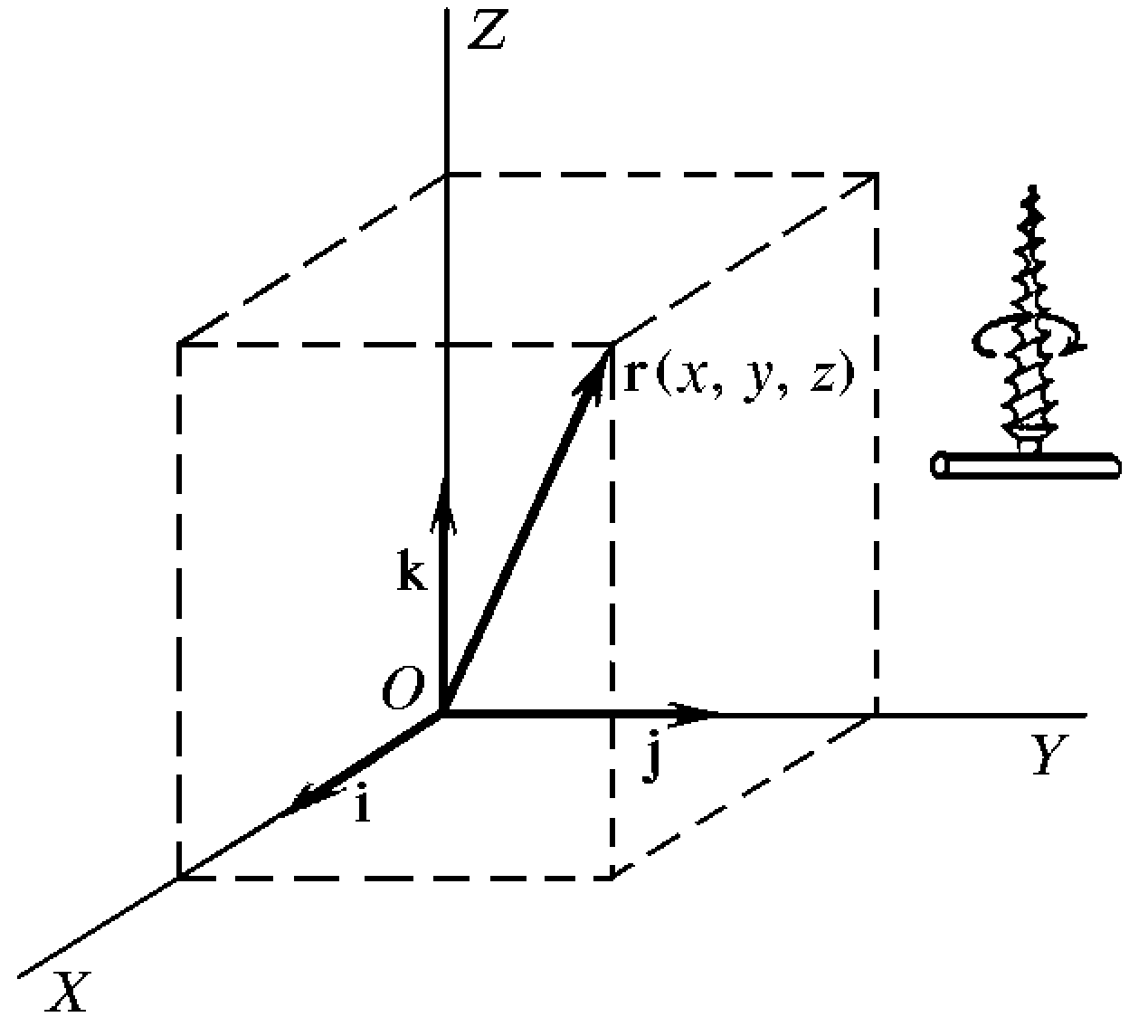 екартовой прямоугольной системы координат. Положение каждой точки в избранной системе отсчета можно задавать тремя числами: , представляющие собой расстояния от этой точки до координатных плоскостей

система отсчета - тело или система тел, относительно которых определяется положение остальных тел.

2. Радиус-вектор - вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой.

Скорость и ускорение материальной точки

средней скоростью МТ:

мгновенной скоростью МТ в момент времени :

,

.

ускорением МТ:

,

или

.

Ускорение также является второй производной координаты по времени и обозначается

.

3. Движение по криволинейной траектории

Перейдем к криволинейному движению МТ. Положение движущейся точки на траектории задается радиус-вектором , проведенным в эту точку из начала координат . В момент времени МТ имеет радиус-вектор . Через короткое время МТ переместилась в положение с радиусом-вектором . Вектор называется перемещением. Отношение этого вектора к изменению времени называется средней скоростью движения за время между и :

Предел средней скорости при , т.е производная радиус-вектора по времени

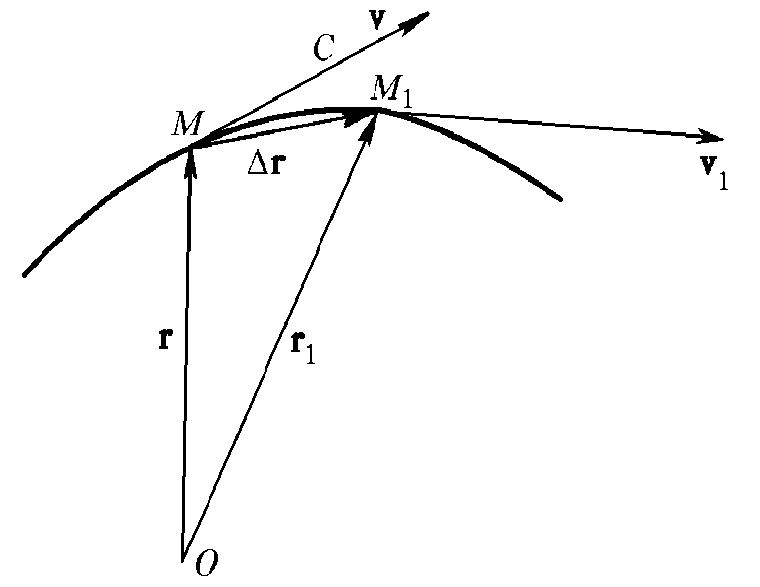н азывается мгновенной скоростью МТ.

Тангенциальное ускорение и нормальное

ускорение на криволинейной траектории представимо в виде:

.

П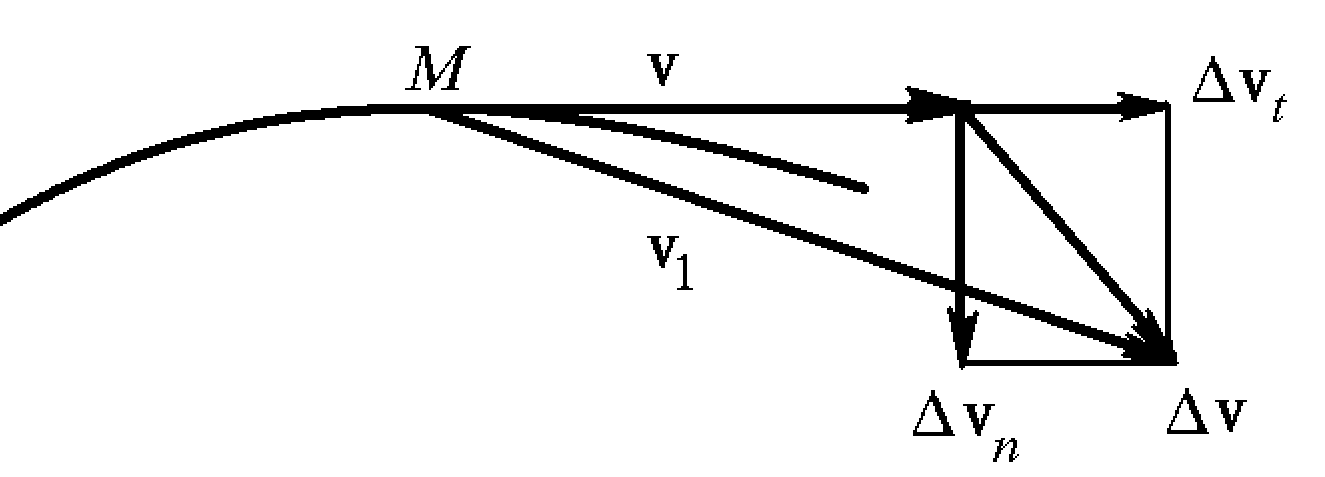 ервый член в этой сумме ответственен за изменение величины скорости и называется тангенциальным ускорением , а второй – за изменение направления скорости и называется нормальным ускорением .

4. Кинема́тика твёрдого тела (от др.-греч. Κίνημα — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

Основными движениями твердого тела являются поступательное движение и вращательное движение вокруг неподвижной оси.

Поступательное движение - это такое движение, при котором любая прямая, связанная с телом, все время остается параллельной своему начальному положению. При поступательном движении все точки твердого тела совершают за один и тот же промежуток времени равные перемещения.

Вращательное движение вокруг неподвижной оси – это движение, при котором одна единственная прямая, связанная с телом, остается неподвижной при движении. Эта прямая и является неподвижной осью, вокруг которой вращаются все точки тела.

угловая скорость

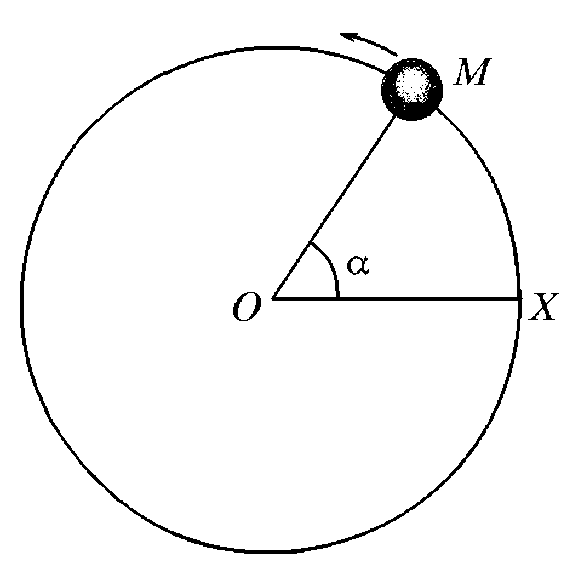Положение точки на окружности можно задать углом , который образует радиус-вектор с каким-либо неизменным направлением. Производная этого угла по времени

называется угловой скоростью. Первая производная угловой скорости или вторая производная угла по времени называется угловым ускорением:

.

Е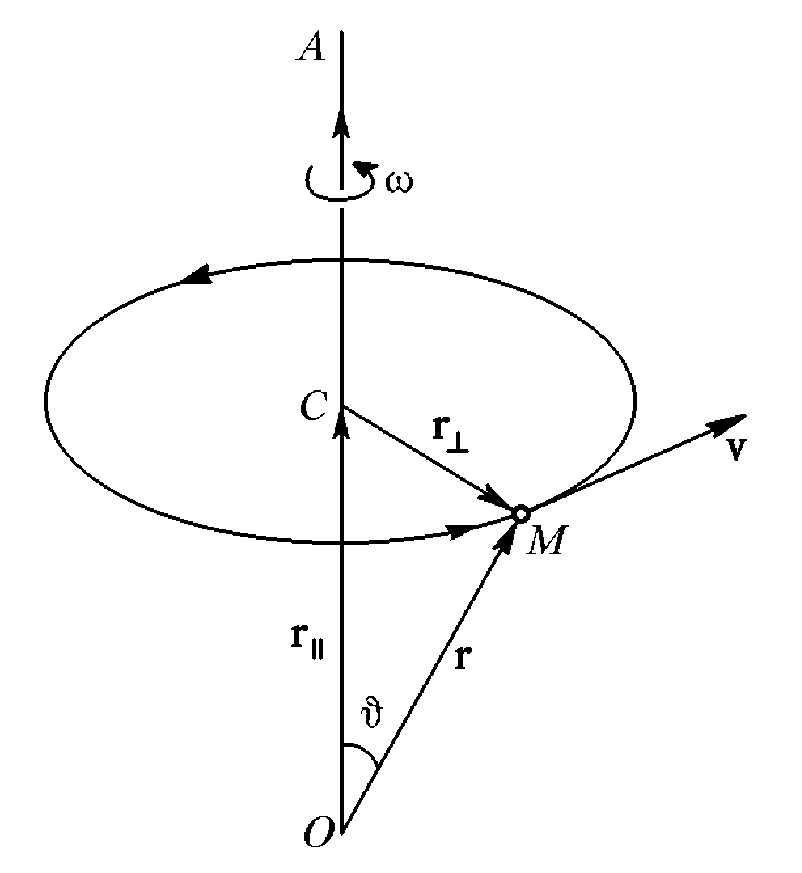 сли аксиальный вектор продифференцировать по времени, то получится новый аксиальный вектор , называемый угловым ускорением.

5. Вопрос 5

Первый закон Ньютона – закон инерции

За первый закон движения Ньютон принял закон инерции: тело, не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным.

Закон инерции не может быть справедлив во всех системах отсчета.

Инерциальная система отсчета - система отсчета, в которой все свободные тела движутся прямолинейно и равномерно.

Земная система отсчета не может быть точно инерциальной, так как Земля испытывает два вращательных движения: вокруг собственной оси и вокруг Солнца. Однако эти движения происходят относительно медленно и для множества движений можно считать, что земная система отсчета инерциальна. Нужны специальные опыты, чтобы вскрыть ее инерциальность.

Гелиоцентрическая система отсчета, оси в которой направлены на почти неподвижные удаленные звезды, еще лучше удовлетворяет требованию инерциальности. В этой системе можно изучать движение тел, малых по сравнению с размерами Галактики.

6. Масса – мера инертности (всякое тело оказывает сопротивление при попытках привести его в движение или изменить модуль или направление его скорости, это свойство называется инертностью).

Импульсом или количеством движения МТ называется вектор, равный произведению массы точки на ее скорость:

.

Импульсом или количеством движения системы материальных точек назовем сумму импульсов отдельных материальных точек:

Сила - всякая причина, изменяющая импульс тела. Это качественное определение.

Второй закон Ньютона: в инерциальной системе отсчета производная импульса МТ по времени равна действующей на нее силе. Для медленных движений и постоянной массе эту формулу можно представить в виде:

7. Третий закон Ньютона

Рассмотрим замкнутую систему, состоящую из двух взаимодействующих МТ. В этом случае справедлив закон сохранения импульса

Дифференцируя это уравнение по времени и использовав второй закон Ньютона, получим:

.

Где и 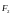— силы, с которыми рассматриваемые МТ действуют друг на друга. третьему закону Ньютона:

Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.

Формулирование задачи движения N материальных точек

Аналогично, можно сформулировать третий закон Ньютона, если МТ много. Для этого рассматриваются отдельно силы взаимодействия отдельных точек друг с другом. Пусть — сила, с которой i-я точка действует на k-ю, — сила, с которой k-я точка действует на i-ю. Третий закон утверждает, что обе эти силы направлены вдоль прямой, соединяющей взаимодействующие точки, причем .

Начальные условия

Для системы из материальных точек необходимо задать начальный радиус-вектор и начальная скорость, т.е. всего векторов или чисел, определяющих начальные значения координат и скоростей материальных точек системы.