Коэффициент безопасности

При расчете отдельных составляющих суммарной тепловой нагрузки необходимо достоверно знать все перечисленные выше условия работы холодильного оборудования и режимы хранения продукции. Однако часто при расчете некоторые из этих параметров остаются неизвестными. В этом случае необходимо задаться некоторыми средними для данного режима работы параметрами и ввести коэффициент для этой составляющей тепловой нагрузки. Другими словами, этот коэффициент является мерой нашего незнания каких-либо условий или режимов работы камеры.

Значение коэффициента безопасности, как правило, находится в пределах от 1,0 до 1,1.

27.Напряженное состояние в точке. Тензор напряжений. Виды напряженного состояния.

Напряженным состоянием в точке тела называют совокупность нормальных икасательных напряжений, возникающих на всевозможных площадках, проходящих через данную точку.

Изучение напряженного состояния начинается того, что в окрестности исследуемой точки, например точки К (рис. 6.1), из нагруженного тела, находящегося в равновесии, мысленно вырезается элементарный параллелепипед со сторонами  ,  и  .

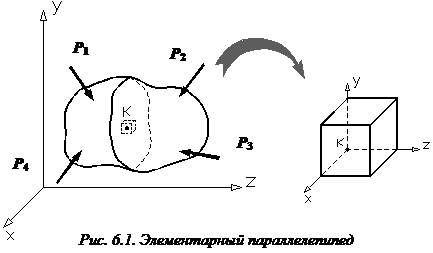 Ввиду малости элементарного параллелепипеда можно считать, что напряженное состояние во всех его внутренних точках одинаково (то есть однородно) и совпадает с напряженным состоянием в непосредственно исследуемой точке К. Предположение, что по граням и по любым сечениям элементарного параллелепипеда нормальные и касательные напряжения распределяются равномерно, позволяют исследовать закон изменениянапряжений по наклонным сечениям элементарного параллелепипеда, считая, что эти сечения проходят через исследуемую точку К.

Те́нзор напряже́ний — тензор второго ранга, состоящий из девяти величин, представляющих механические напряжения в произвольной точке нагруженного тела. Эти девять величин записываются в виде таблицы, в которой по главной диагонали стоят нормальные напряжения в трёх взаимно перпендикулярных осях, а в остальных позициях — касательные напряжения, действующие на трёх взаимно перпендикулярных плоскостях.

Виды Напряженного Состояния В Точке Сопромат

В дальнейшем мы увидим, что в окрестности любой точки деформированного твердого тела всегда можно выделить элементарный параллелепипед, ориентированный в пространстве таким образом, что по его граням будут возникать только нормальные напряжения.

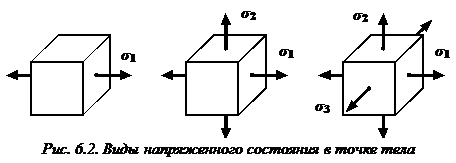
В зависимости от того, испытывает параллелепипед «растяжение» («сжатие») в одном, в двух или в трех направлениях (рис. 6.2), различают виды напряженного состояния:

линейное (одноосное) напряженное состояние,

плоское (двухосное) напряженное состояние,

объемное (трехосное) напряженное состояние.

С линейным напряженным состоянием мы уже сталкивались при изучении центрального растяжения (сжатия).

 В задачах сопроматачасто встречается плоское напряженное состояние. Его характерным признаком является полное отсутствие нормальных и касательных напряжений на двух параллельных гранях параллелепипеда.

Будем полагать, что при плоском напряженном состоянии напряжения не возникают на гранях элементарного параллелепипеда с нормалью x. Тогда вместо объемного параллелепипеда с целью упрощения, мы будем на рисунках показывать проекцию параллелепипеда на плоскость  . (штриховкой будем указывать внутреннюю область элемента).

Объемное напряженное состояние в курсе сопротивления материалов практически не изучается.