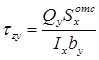61.Расчёт вала на жесткость при кручении.

- условия жесткости:

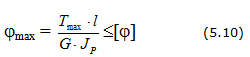
В качестве примера можно указать на ходовые винты токарных станков, при деформации которых шаг их резьбы изменяется, а, следовательно, и шаг резьбы, нарезанной на этом станке, получается с некоторой погрешностью. допускаемый угол закручивания зависит от назначения вала.

62.Статически неопределимые системы при кручении. Статически неопределимыми называются такие системы, опорные реакции в которых и (или) внутренние усилия невозможно определить только из уравнений статики (уравнений равновесия).По сравнению с системами статически определимыми указанные системы имеют дополнительные связи, которые называют лишними связями. Усилия, возникающие в лишних связях, называют лишними неизвестными.Термин «лишние» следует понимать как «избыточные», а не как «ненужные». Наличие лишних связей делает систему более жёсткой и более экономичной.Степенью статической неопределимости n называется разность между числом неизвестных искомых усилий Н и числом независимых уравнений равновесия У для их нахождения: n = Н – У.Для расчета статически неопределимых систем применяют несколько методов, из которых в сопротивлении материалов рассматривают метод сил.

63.Потенциальная энергия деформации при кручении. При кручении, так же как и при других видах деформации бруса, работа внешних сил (скручивающих моментов) расходуется на создание в деформированном теле определенного запаса энергии (потенциальной энергии деформации).

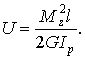
При ступенчатом изменении сечения или крутящего момента

В случае, если или (или обе эти величины) изменяются по длине отдельных участков непрерывно, следует пользоваться формулой

64.Виды изгибов.Опоры и опорные реакции.

Изгиб-способ деформации твердого тела, под влиянием действующих на него внешних сил, при котором изменяется кривизна какой-либо его геометрической оси.Виды изгиба:плоский,косой и прмой. Реакциями опор называют усилия, возникающие в опорах и удерживающие элемент находящийся под действием внешних нагрузок в состоянии статического равновесия.Типы опор:шарнирно-подвижна,шарнирно-неподвижная,жесткая заделка.Проще говоря, опорные реакции это ровно те силы и моменты, которые необходимы для того, чтобы брус на который действует система заданных внешних нагрузок не вращался и не перемещался в пространстве. При этом, многие задачи в сопромате легко решаются без их определения. Это возможно в случаях, когда за расчетную схему принимается брус заделанный в жесткую опору (заделку) без дополнительных опор, например статически определимая консольная балка или стержень либо стержневая система. В общем случае любую жесткую подвижную систему можно остановить приложив к ней одну силу и один момент. Это собственно и есть минимально необходимое число связей, обеспечивающее статическое равновесие системы. когда все внешние нагрузки лежат в одной плоскости, количество реакций в общем случае сокращается до трех: двух сил (вертикальной Ry и горизонтальной Rz) и момента Mx. При растяжении-сжатии, для удержания бруса в статичном состоянии достаточно одной силы, приложенной вдоль его оси. Из условия, что заданная система не перемещается в пространстве (вправо-влево, вверх-вниз, а также, вперед-назад) можем приравнять к нулю сумму проекций всех сил на оси x, y и z.∑F(x)=0; ∑F(y)=0; ∑F(z)=0. Из условия, что система не вращается, приравниваем к нулю сумму моментов, создаваемых всеми нагрузками относительно соответствующих осей.∑m(x)=0; ∑m(y)=0; ∑m(z)=0. Если твердое тело находится в состоянии покоя (обычно в сопромате рассматривают такие конструкции) то приложенные к этому телу внешние силы взаимно уравновешены. При этом обязательно учитываются ВСЕ внешние силы, т е и заданная нагрузка и реакции опор; и жениопределения реакций опор выбирают такие уравнения равновесия, в каждое из которых входит не более 1 неизвестной реакции (если это удается). В строительной механике определяют так называемые МОМЕНТНЫЕ ТОЧКИ (точки, в которых пересекаются линии действия двух и более опорных реакций). Составляя уравнение равновесия в виде суммы моментов относительно моментной точки, мы избавляемся от нескольких "лишних" неизвестных.Составляя уравнение равновесия: сумма моментов относительно шарнирной опоры мы получаем полезное уравнение, так как избавились от одного - двух неизвестных.

65.Напряжени в поперечных сечениях балок при чистом изгибе.Эпюры напряжений. Если изгибающий момент Mx является единственным внутренним силовым фактором, то такой изгиб называется чистым. При наличии поперечной силы изгиб называется поперечным.Брус, работающий при изгибе, называется балкой.При поперечном изгибе в сечении балки помимо изгибающего момента () возникает поперечная сила (). Поэтому в поперечном сечении при поперечном изгибе наряду с нормальными напряжениями () возникают и касательные напряжения ().На основании закона парности касательные напряжения возникают и в продольных сечениях балки. Вследствие этого при поперечном изгибе отмечаются сдвиги продольных слоев балки относительно друг друга.При поперечном изгибе гипотеза плоских сечений нарушается, поскольку поперечные сечения балки искривляются . Исследования показали: если балка является достаточно длинной, влияние искривления поперечного сечения на значения нормальных напряжений невелико, поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают, формула нормальных напряжений при поперечном изгибе: .

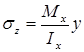
Проанализируем формулу Журавского: