4 Метод сечений для определения внутренних усилий

Определяются внутренние силы с помощью метода сечений. Суть метода сечения в следующем: если при действии внешних сил тело находится в состоянии равновесия, то любая отсеченная часть тела вместе с приходящимися на нее внешними и внутренними усилиями также будет находится в равновесии, следовательно, к ней применимы уравнения равновесия. То есть, внутренние силы не влияют на условия равновесия тела, так как являются самоуравновешенными.

Рассмотрим тело, к которому приложена некоторая система внешних сил F₁, F₂, …, F_n, удовлетворяющая условиям равновесия, т.е. при действии указанных внешних сил тело находится в состоянии равновесия. Если необходимо, то определяются опорные реакции из уравнений равновесия (берем объект, отбрасываем связи, заменяем отброшенные связи реакциями, составляем уравнения равновесия и решаем систему). Реакции можно не находить, если они не входят в число внешних сил, приложенных по одну сторону от рассматриваемых сечений.

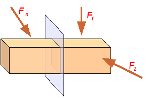Мысленно рассекаем тело произвольным сечением, отбрасываем левую часть тела и рассматриваем равновесие оставшейся части.

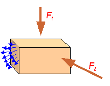Если бы не было внутренних сил, оставшаяся неуравновешенная часть тела начала бы двигаться под действием внешних сил. Для сохранения равновесия, действие отброшенной части тела заменяем внутренними силами приложенными к каждой частице тела.

5 Продольные силы и их эпюры

Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение  ).

КАК СТРОИТЬ ЭПЮРУ ПРОДОЛЬНЫХ СИЛ?

Для построении эпюры N используется метод сечений. Продемонстрируем его применение на примере (рис. 2.1).

 Определим продольную силу N, возникающую в намеченном нами поперечном сечении стержня.

Разрежем стержень в этом месте и мысленно отбросим нижнюю его часть (рис. 2.1, а). Далее мы должны заменить действие отброшенной части на верхнюю часть стержня внутренней продольной силой N.

Для удобства вычисления ее значения закроем рассматриваемую нами верхнюю часть стержня листком бумаги. Напомним, что продольное усилие N, возникающее в поперечном сечении, можно определить как алгебраическую сумму всех продольных сил, действующих на отброшенную часть стержня, то есть на ту часть стержня, которую мы видим.

При этом применяем следующее правило знаков: силы, вызывающие растяжение оставленной части стержня (закрытой нами листком бумаги) входят в упомянутую алгебраическую сумму со знаком «плюс», а силы, вызывающие сжатие – со знаком «минус».

6. Поперечная сила и изгибающий момент.

Поперечным изгибом называется такой вид деформирования бруса, при котором внешние нагрузки действуют перпендикулярно к его продольной оси. Деформация изгиба заключается в искривлении оси бруса. Брус с прямой осью, работающий на изгиб, называется балкой. Если плоскость действия внешних нагрузок проходит через ось балки и одну из главных центральных осей поперечного сечения, изгиб называется прямым. В этом случае ось балки искривляется в плоскости действия нагрузок и является плоской кривой.

В сечениях балки возникают два внутренних силовых фактора: изгибающий момент М_х и поперечная сила Q_y

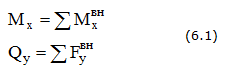
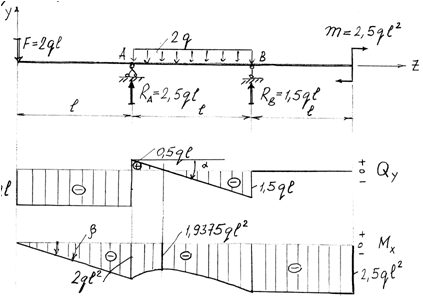
Правила контроля построения эпюр Q и М при изгибе (рис. 6.1). 

Дифференциальные зависимости между q, Q_y и М_х имеют вид:

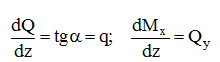
1. В сечении, где приложена сосредоточенная сила, - на эпюре Q_y скачок по модулю равный этой силе, на эпюре М_х – излом навстречу силе.

2. В сечении, где приложена сосредоточенная пара сил, - на эпюре М_х скачок по модулю равный этой паре сил. На эпюре Q_y это не сказывается.

3.Если на участке имеется равномерно распределенная нагрузка, то Q_y изменяется по линейному закону, М_х – по параболе, выпуклостью навстречу нагрузке q (М_х = М_экстр – в сечении, где Q_y меняет свой знак).

7 Взаимосвязь между крутящим моментом, поперечной силой и интенсивностью распределенной нагрузки

Между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки легко установить определенную зависимость. Рассмотрим балку, нагруженную произвольной нагрузкой (рисунок 5.10). Определим поперечную силу в произвольном сечении, отстоящем от левой опоры на расстоянии Z. Проецируя на вертикаль силы, расположенные левее сечения, получаем  (5.1) Вычисляем поперечную силу в сечении, рас­положенном на расстоянии z + dz от левой опоры.  (5.2) 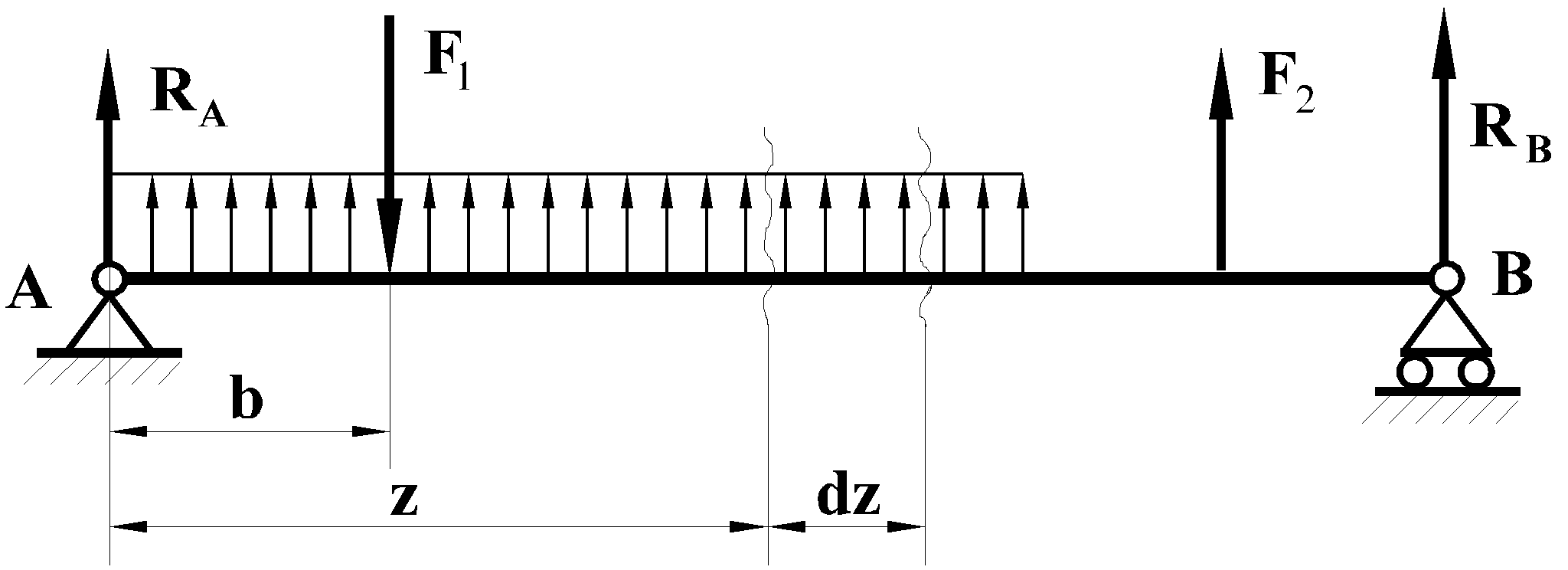Рисунок 5.8. Вычитая (5.1) из (5.2) получаем dQ = qdz, откуда то есть производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки. Вычислим теперь изгибающий момент в сечении с абсциссой z, взяв сумму моментов сил, приложенных слева от сечения. Для этого распределенную нагрузку на участке длиной z заменяем ее равнодействующей, равной qz и приложенной в середине участка, на расстоянии z/2 от сечения:  (5.3)   (5.4) Вычитая (5.3) из (5.4), получаем приращение изгибающего момента Выражение в скобках представляет собой поперечную силу Q. Тогда  . Отсюда получаем формулу  (5.5) Таким образом, производная от изгибающего момента по абсциссе сечения балки равна поперечной силе (теорема Журавского).  Взяв производную от обеих частей равенства (5.5), получим