
5.5. Вектор-функция скалярного аргумента. Кривые в пространстве и на плоскости
Определение
вектор функции. Определение 8.
Функция,
заданная на некотором подмножестве
 ,
значениями которой является некоторое
множество векторов,
,
значениями которой является некоторое
множество векторов,
 ,(
,(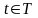 )
называется векторной
функцией скалярного аргумента
(вектор-функция).
)
называется векторной
функцией скалярного аргумента
(вектор-функция).
В этом определение
в зависимости от задачи под значениями
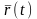 можно понимать как свободные вектора,
так и вектора с закрепленным началом.
можно понимать как свободные вектора,
так и вектора с закрепленным началом.
Если
в пространстве задана декартовая система
координат, то вектору соответствует
некоторая упорядоченная тройка
чисел-координат и наоборот, каждой
тройке чисел соответствует вектор.
Поэтому задание вектор-функции
эквивалентно заданию трех скалярных
функций
 ,
,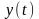 ,
,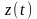 ,которые
являются его координатами:
,которые
являются его координатами:

 ,
,
,
,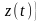 .
.
На
плоскости
; .Будем
предполагать, что для вектор-функции
справедливы все свойства векторов,
определенные линейными операциями
векторов, скалярным и векторным
произведением.
.Будем
предполагать, что для вектор-функции
справедливы все свойства векторов,
определенные линейными операциями
векторов, скалярным и векторным
произведением.
Длину
вектора будем обозначать
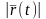
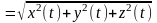 .
.
Замечание.
Можно рассматривать векторные функции
в
-мерном
пространстве
 т.е.
т.е.
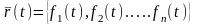 .
Но в дальнейшем все будем рассматривать
для
.
Но в дальнейшем все будем рассматривать
для
 .
.
Пусть
определена
в некоторой окрестности точки
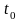 и
и
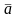 -некоторый
вектор.
-некоторый
вектор.
Определение 9. Вектор называется пределом вектор-функции , если
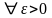
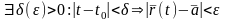
 .
.
Или

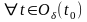 .
.
Обозначение
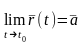 .
.
Теорема
12. Пусть
 ,
,
,
.
Для того чтобы вектор
,
,
,
.
Для того чтобы вектор
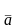 являлся пределом
являлся пределом
 в точке
необходимо
и достаточно, чтобы
в точке
необходимо
и достаточно, чтобы
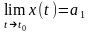
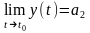
 .
.
Для векторов справедливо свойства пределов сумм, разности, скалярного и векторного произведения.
1.Если
,
то
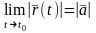 .
Это следует из неравенства
.
Это следует из неравенства
 .
.
2.
 .
.
3.
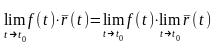 ,
где
,
где
 -скалярная
функция.
-скалярная
функция.
4.
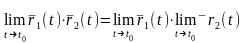 .
.
5.
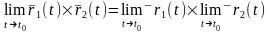 .
.
В свойствах 2-5 все рассматриваемые функции определены на некотором множестве и предполагается, что все пределы, входящие в правые части существуют. Доказывается аналогично доказательству пределов для скалярных функций.
Определение
10.
Вектор-функция
,
определенная в некоторой окрестности
точки
называется непрерывной
в точке
,
если
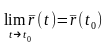 .
.
Из теоремы 12
очевидно, что непрерывность
эквивалентна непрерывности в точке
трех
скалярных функций
 и справедливы свойства с арифметическими
операциями над непрерывными функциями.
и справедливы свойства с арифметическими
операциями над непрерывными функциями.
Определение
11. Пусть
векторная функция
определена в некоторой окрестности
точки
.
Если существует предел
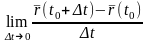 или
или
 (
(
 ),
то он называется производной
данной
векторной функции в точке
и обозначается
),
то он называется производной
данной
векторной функции в точке
и обозначается
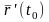 или
или
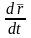 .
.
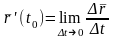 ,
(
,
( ).
).
Производная является тоже вектором. Вектор-функция, имеющая производную в точке называется дифференцируемой в этой точке. Видно, что определение производной вектор-функции аналогично определению производной скалярной функции.
Легко показать,
что если выбрана декартова система
координат и
 ,
то
,
то
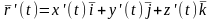 ,
при условии что
,
при условии что
 дифференцируемы по
дифференцируемы по
 функции. Это следует из того, что
функции. Это следует из того, что
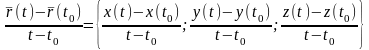 и дальше по теореме
12.
и дальше по теореме
12.
Производную
 вектор-функции
называется так же скоростью
изменения вектора
относительно параметра
.Если
длина
не изменяется производная
называется также скоростью
вращения
вектора
.
вектор-функции
называется так же скоростью
изменения вектора
относительно параметра
.Если
длина
не изменяется производная
называется также скоростью
вращения
вектора
.
Производная вектор функции обладает следующими свойствами, аналогичным свойствам скалярных функций.
1. Если вектор функция дифференцируема в точке , то она непрерывна в этой точке.
2.
Если
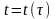 -
дифференцируема в точке
-
дифференцируема в точке
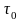 скалярная функция,
дифференцируема в точке
скалярная функция,
дифференцируема в точке
 векторная функция, то справедлива
следующая формула
векторная функция, то справедлива
следующая формула
 или короче
или короче

3.
Если
 дифференцируемы, то
дифференцируемы, то




Производные высших
порядков для вектор-функций определяются
по индукции: если у вектор-функции
в некоторой окрестности точки
существует производная
 порядка
(
порядка
( ,
то производная порядка
,
то производная порядка
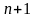 в этой точке определяется по формуле:
в этой точке определяется по формуле:
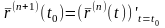 .
.
Если , , -раз дифференцируема в некоторой окрестности , то имеет место формула
 ,
,
или
 ,
,
которая называется формулой Тейлора для вектор-функции с остаточным членом в форме Пеано. Эта формула непосредственно следует из разложения по формуле Тейлора координат .
Из всего этого
видно, что рассмотренные понятия и
утверждения для векторных функций
получается перенесением соответствующих
понятий и утверждений для скалярных
функций. Однако следует отметить, что
не все что справедливо для скалярной
функции имеет прямой аналог для
вектор-функции. Например, для вектор-функции
несправедлива теорема Ролля, а
следовательно теорема Лагранжа, частным
случае которой является теорема Ролля.
Например,

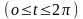 -
дифференцируема функция.
-
дифференцируема функция.
 ,
,
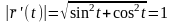
 .
.
Однако
не существует
 ,
для которой
,
для которой
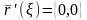 ,
несмотря на то, что
,
несмотря на то, что
 .
.
Для векторных функций вместо прямого аналога теоремы Лагранжа имеет место следующая теорема.
Теорема
13. Если
вектор-функция
непрерывна на отрезке
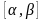 и дифференцируема внутри него, то
существует точка
и дифференцируема внутри него, то
существует точка
 ,
такая, что
,
такая, что
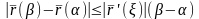 (10)
(10)
□
Если
 ,
то (10) выполняется автоматически.
Пусть
,
то (10) выполняется автоматически.
Пусть
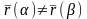

 .
Пусть
.
Пусть
 -единичный
вектор (
-единичный
вектор (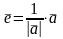 ),
одинаково направленный с
),
одинаково направленный с
 (т.к.
(т.к.
 где
-единичный
вектор),
где
-единичный
вектор),
 -скалярное
произведение. Т.о., получилась разность
значений скалярной функции
-скалярное
произведение. Т.о., получилась разность
значений скалярной функции
 на концах отрезка
:
на концах отрезка
:
 .
.
Из этой формулы
следует, что
 непрерывна на отрезке
и дифференцирована в
непрерывна на отрезке
и дифференцирована в
 ,
т.к. по условию этим обладает функция
.
Тогда для
справедлива формула Лагранжа:
,
т.к. по условию этим обладает функция
.
Тогда для
справедлива формула Лагранжа:
 ,
,
 .
.
Но по правилу
дифференцирования скалярного произведения
имеем
 ,
поэтому
,
поэтому
 ,
но т.к.
,
но т.к.
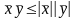 ,
то
,
то
 .
■
.
■
Кривые на плоскости
и в пространстве. Пусть
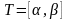 некоторый отрезок
некоторый отрезок
 .Тогда
векторная функция,
заданная на
,
есть отображение этого отрезка в
,
т.е.
:
.Тогда
векторная функция,
заданная на
,
есть отображение этого отрезка в
,
т.е.
:
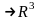 .
Если
непрерывна
в каждой точке
,
то
.
Если
непрерывна
в каждой точке
,
то
 непрерывна на отрезке
.
непрерывна на отрезке
.
Определение
12. Непрерывное
отображение
отрезка
в пространство или на плоскость называется
кривой.
Число
называется параметром
кривой. Кривые будем обозначать
 ,
т.е.
,
т.е.
 .
.
Само множество
точек на плоскости или в пространстве
называется носителем
кривой
 .
Отметим, что, во-первых, одно и то же
множество, полученное как образ двух
разных непрерывных отображений отрезков,
рассматриваются как различные кривые.
.
Отметим, что, во-первых, одно и то же
множество, полученное как образ двух
разных непрерывных отображений отрезков,
рассматриваются как различные кривые.
Во-вторых, непрерывное
отображение, которое является кривой,
не предполагается взаимно-однозначным,
т.е. в одну точку кривой
может отобразиться две или боле точек
.
Точки
,
в которые, отображается несколько точек
,
называются точками
самопересечения.
Точка носителя кривой, в которую,
отображается по крайне мере две точки
отрезка
,
называется кратной
точкой носителя
или точкой
самопересечения.
Точка
 называется началом кривой, точка
называется началом кривой, точка
 концом кривой.
концом кривой.
Определение
13. Кривая
называется замкнутой
кривой или
замкнутым
контуром,
если ее начало совпадает с концом, т.е.
.Замкнутая
кривая, не имеющая точек самопересечения,
кроме точек
и такая, что
 при
при
 называется простым
замкнутым контуром.
Если кривая
не имеет точек самопересечения, называется
просто дугой.
называется простым
замкнутым контуром.
Если кривая
не имеет точек самопересечения, называется
просто дугой.
Если
кривая
задана вектор-функцией
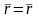 ,
,
,
то это эквивалентно заданию трех
скалярных функций:
,
,
,
то это эквивалентно заданию трех
скалярных функций:

 .
.
Такое задание кривой называется параметрическим.
Пример 10.
1
z
)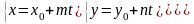 -
прямая линия в пространстве.
-
прямая линия в пространстве.
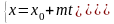 -
прямая линия на плоскости.
-
прямая линия на плоскости.
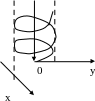
2
a
)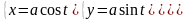 -
винтовая линия (рис.10).
-
винтовая линия (рис.10).
Рис.10
3)
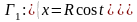



Это две разные
кривые носителем является одна и та же
окружность
 ,
но в первом случае
,
но в первом случае
 и окружность проходиться один раз. А в
и окружность проходиться один раз. А в

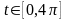 и окружность проходится два раза. Кривая
и окружность проходится два раза. Кривая
 имеет
одну кратную точку, а у
все точки кратные.
имеет
одну кратную точку, а у
все точки кратные.
4)
Кривая

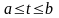 является просто дугой, если
непрерывная
на
.
Носителем является график
.
является просто дугой, если
непрерывная
на
.
Носителем является график
.
Определение 14. Кривая заданная вектор-функцией на называется непрерывно-дифференцируемой, если непрерывно дифференцируема функция , т.е. следующие функции на .
Непрерывно-дифференцируемая
кривая называется
гладкой,
если

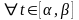 .
Кривая
называется кусочно-гладкой,
если ее можно представить как конечную
сумму гладких кривых.
.
Кривая
называется кусочно-гладкой,
если ее можно представить как конечную
сумму гладких кривых.
Лемма.
В каждой
точке гладкой кривой
 существует касательная, и производная
вектор-функции
направлена по этой касательной в сторону
возрастая параметра.
существует касательная, и производная
вектор-функции
направлена по этой касательной в сторону
возрастая параметра.
□
Пусть
возрастает при движении от
 к
к
 (рис.11а). Вектор
(рис.11а). Вектор
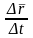 направлен по секущей
направлен по секущей
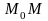 .
По условию производная существует, т.е.
.
По условию производная существует, т.е.
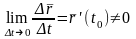 .
Откуда
направлен по касательной. Векторы
.
Откуда
направлен по касательной. Векторы
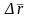 и
лежат на одном и том же луче
и
лежат на одном и том же луче
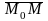 .
Если
.
Если
 ,
то векторы
и
направлены в сторону возрастания
параметра
.
Если
,
то векторы
и
направлены в сторону возрастания
параметра
.
Если
 (рис.11б),
то
направлен в сторону убывания параметра
,
а вектор
снова направлен в сторону возрастания
.
■
(рис.11б),
то
направлен в сторону убывания параметра
,
а вектор
снова направлен в сторону возрастания
.
■



Рис.11а
Рис.11б
Пусть кривая задана
параметрическими уравнениями. Напишем
уравнение касательной прямой в точке
 которая соответствует значению параметра
,
которая соответствует значению параметра
,
 .
Если кривая гладкая, то
.
Если кривая гладкая, то
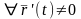 .
.
Каноническое
уравнение прямой имеет вид:
 .
.
Вектор
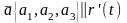 ,
тогда уравнение касательной прямой:
,
тогда уравнение касательной прямой:
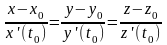 .
.
Определение 15. Нормальной плоскостью к пространственной кривой называется плоскость перпендикулярная касательной прямой и проходящей через точку касания.
Пусть
точка касания. Уравнение плоскости
 ,
где
,
где
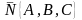 -
нормальный вектор. Но вектор
-
нормальный вектор. Но вектор
 ,
следовательно, за
,
следовательно, за
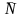 можно
взять
.
Тогда уравнение нормальной плоскости
будет иметь вид:
можно
взять
.
Тогда уравнение нормальной плоскости
будет иметь вид:
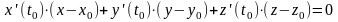 .
.
Пример
11. Найти
уравнение касательной прямой и нормальной
плоскости к винтовой линии в точке
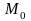 ,
где
,
где
 .
.
Спрямляемые
кривые. Длина кривой.  отрезка
называется множество точек
отрезка
называется множество точек
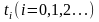 таких, что
таких, что
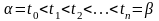 ;
;
 .
Пусть
кривая, заданная вектор-функцией
на отрезке
,
т.е.
.
Пусть
кривая, заданная вектор-функцией
на отрезке
,
т.е.
 .
.
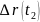

Рис.13
Обозначим
 ,
т.е.
,
т.е.
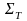 –
длина ломаной с вершинами в точках
–
длина ломаной с вершинами в точках
 ,
являющимися концами радиус-векторов
,
являющимися концами радиус-векторов
 ,
иначе говоря , ломанной, вписанной в
кривую
(рис.13).
,
иначе говоря , ломанной, вписанной в
кривую
(рис.13).
Определение 17. Точная верхняя грань на множестве T длин всевозможных ломанных, вписанных в данную кривую, называется длиной этой кривой.
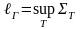 .
.
Если
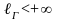 ,
то кривая
называется
спрямляемой.
Бывают и не спрямляемые кривые. Но они
задаются очень сложно, и примеры приводить
не будем.
,
то кривая
называется
спрямляемой.
Бывают и не спрямляемые кривые. Но они
задаются очень сложно, и примеры приводить
не будем.
Теорема
14. Если кривая
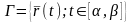 непрерывно дифференцируемая, то она
спрямляемая и ее длина
непрерывно дифференцируемая, то она
спрямляемая и ее длина
 удовлетворяет неравенству:
удовлетворяет неравенству:
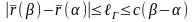 ,
где
,
где
 .
(11)
.
(11)
□
Пусть
некоторое разбиение
.
Можно записать
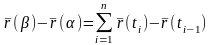 и применяя теорему 13, получим:
и применяя теорему 13, получим:

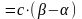 ,
где
,
где
 ;
;
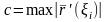 .
.
т.к.
 - длина ломаной, вписанной в кривую
,
соответствующая разбиению
,
то из последнего равенства следует, что
- длина ломаной, вписанной в кривую
,
соответствующая разбиению
,
то из последнего равенства следует, что
 .
.
Перейдя в этом неравенстве к верхней грани по все возможным разбиением отрезка , получим в силу определения 17 неравенство:
 .
.
В заключение
отметим, что в силу непрерывной
дифференцированности функции
на
числовая функция
 непрерывна на этом отрезке и, следовательно,
по теореме Вейерштрасса принимает на
нем наибольшее значение в некоторой
точке
:
непрерывна на этом отрезке и, следовательно,
по теореме Вейерштрасса принимает на
нем наибольшее значение в некоторой
точке
:
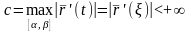 .
.
Поэтому
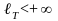 ,
т.е.
-спрямляемая
кривая. ■
,
т.е.
-спрямляемая
кривая. ■
Теорема
15. Если
кривая
 непрерывно дифференцируемая, то
переменная длина дуги
непрерывно дифференцируемая, то
переменная длина дуги
 ,
отсчитываемая от начала кривой
,
является возрастающей непрерывно
дифференцируемой функцией параметра
и
,
отсчитываемая от начала кривой
,
является возрастающей непрерывно
дифференцируемой функцией параметра
и
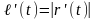 ,
т.е.
,
т.е.
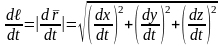
или
 .
(12)
.
(12)
□
Пусть
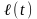 длина дуги кривой
от
точки
длина дуги кривой
от
точки
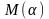 до точки
до точки
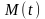 ,
,
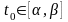 ;
;
 .
Тогда
.
Тогда
 -
длина дуги от точки
-
длина дуги от точки
 до
до
 .
Поэтому по теореме 14, имеем из (11):
.
Поэтому по теореме 14, имеем из (11):
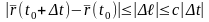 ,
,
где
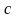 наибольшее значение
на отрезке
наибольшее значение
на отрезке
 .
.
Обозначим через
точку,
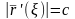 .
Разделим обе части равенства на
.
Разделим обе части равенства на
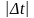 :
:
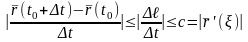 ,
,
но возрастает с ростом , т.к. длина дуги увеличивается, т.о.
 (13)
(13)
Левая и правая
часть равенства имеют один и тот же
предел при
 .
Действительно, по определению производной
имеем:
.
Действительно, по определению производной
имеем:
 ,
,
В
правой части, т.к.
 ,
то при
,
то при
 ,
,
,
,
 .
А т.к. функция
непрерывна в точке
,
то
.
А т.к. функция
непрерывна в точке
,
то
 .
.
И
тогда из неравенства (13) получаем, что
предел
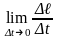 существует и равен
существует и равен
 .
Это означает, что существует производная
.
Это означает, что существует производная
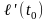 ,
и что
,
и что
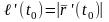 .
Тогда, если
.
Тогда, если
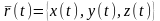 ,
то
.
■
,
то
.
■
Замечания.
1.
Ясно, что
если рассматривается кривая на плоскости,
то
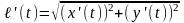 .
.
2.
Если умножить
обе части (12) на
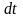 ,
то выражение
,
то выражение
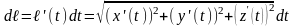 называется
дифференциалом
дуги.
называется
дифференциалом
дуги.
3. Если кривая
задана в явном виде на плоскости
,
то параметризируя уравнение кривой:
,
для дифференциала дуги получим на
плоскости
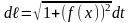 .
.
