
Глава 5. Приложения производной
5.1. Правило Лопиталя
Наряду с основным
приемом нахождения пределов функции -
методом выделения главной части,
существуют и другие способы отыскания
пределов. Здесь будут представлены три
теоремы, с помощью которых можно находить
пределы типа .
.
Теорема
1. Пусть
функции
 и
и
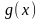 удовлетворяют условиям:
удовлетворяют условиям:
а)
определены и дифференцируемы в некоторой
окрестности точки
 за исключением может быть самой точки
за исключением может быть самой точки
 ;
;
б)
пусть также
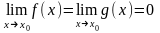 ;
;
в)
 в проколотой окрестности точки
;
в проколотой окрестности точки
;
г)
существует
 ,
,
тогда
существует
,
причем

□
По условию
 и
и
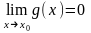 .
Доопределим
и
в точке
.
Доопределим
и
в точке
 ,
а именно положим
,
а именно положим
 .
Так как
и
дифференцируемы в окрестности точки
.
Так как
и
дифференцируемы в окрестности точки
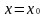 ,
то они непрерывны в этой окрестности
точки
,
то есть на отрезке
,
то они непрерывны в этой окрестности
точки
,
то есть на отрезке
 .
По условию,
откуда
следует, что
.
По условию,
откуда
следует, что при
при
 .
Тогда можно записать формулу Коши на
сегменте
.
.
Тогда можно записать формулу Коши на
сегменте
.


 .
.
Если
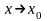 ,
то
,
то
 +0,
следовательно
+0,
следовательно
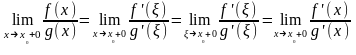 .
Аналогично, если
и
.
Аналогично, если
и
 .
■
.
■
Теорема 2. Пусть функции и удовлетворяют условиям :
а) определены и
дифференцируемы при
 :
:
б)
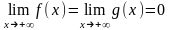 :
:
в)
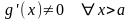 :
:
г) существует
предел
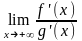 ,
,
Тогда существует
и предел
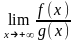 , причем они равны, т.е.
, причем они равны, т.е.

□
Без ограничения
общности можно считать, что
 .
Сделаем замену
.
Сделаем замену
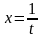 .
Тогда, очевидно, что функции
.
Тогда, очевидно, что функции
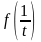 и
и
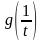 определены в интервале
определены в интервале
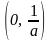 и
и
 .
.
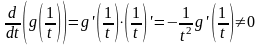 ,
,
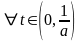 .
.
Тогда
в силу теоремы 1, имеем :
 .
.
Теорема
справедлива, и если
 .
■
.
■
Теорема 3. Пусть функции и :
а) определены и дифференцируемы в окрестности точки , за исключением может быть самой точки ;
б)
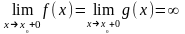 ;
;
в)
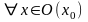 ;
;
г) существует
предел

 .
.
Тогда существует
предел
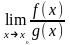 ,
причем
,
причем
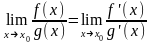 .
.
Замечание 1. В силу теорем 1-3 существует общий способ нахождения предела отношения двух функций, основанный на равенстве . Этот способ называется правилом Лопиталя.
Замечание
2. Если для
производных
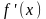 и
и
 выполняют условия теорем 1-3, то правило
Лопиталя можно применить повторно, т.е.
выполняют условия теорем 1-3, то правило
Лопиталя можно применить повторно, т.е.
 .
.
Пример 1. Вычислить пределы с помощью правила Лопиталя:
1)
 .
2)
.
2)
 .
3)
.
3)

 .
.
Кроме неопределенностей
 и
и
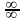 встречаются еще неопределенности других
типов.
встречаются еще неопределенности других
типов.
Под раскрытием
неопределенности типа
 понимают нахождение предела
понимают нахождение предела
 ,
когда
,
когда
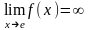 и
и
 .
.
Под неопределенностью
типа
 понимают нахождение предела
понимают нахождение предела
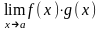 ,
если
,
если

 и
и
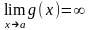 .
.
Есть
и другие неопределенности:
 ;
;
 ;
;
 .
.
Неопределенности типа и сводятся к неопределенностям или путем алгебраических преобразований.
Другие неопределенности
обычно сводятся к неопределенностям
или
путем логарифмирования выражения
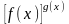
Пример 2. Вычислить пределы с помощью правила Лопиталя:
1)
 ;
2)
;
2)
 ;
3)
;
3)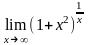 ;
;
4)
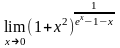 .
.
5.2. Формула Тейлора
Здесь будет доказана формула, которая является одной из основных в математическом анализе и имеет многочисленные приложения, как в самом анализе, так и в других дисциплинах.
Теорема
4. (Тейлор).
Пусть функция
имеет в некоторой окрестности т.
(n+1)-ю
производную,
x
– любое значение аргумента из этой
окрестности и p
– произвольное положительное число.
Тогда между точками
 и
найдется
также точка
и
найдется
также точка
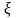 ,
что будет справедлива формула Тейлора.
,
что будет справедлива формула Тейлора.
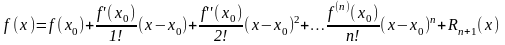 ,
(1)
,
(1)
где
 .
(2)
.
(2)
Выражение
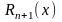 называется
остаточным
членом в формуле Тейлора,
записанным в общей форме или в форме
Шлемильха-Роша.
называется
остаточным
членом в формуле Тейлора,
записанным в общей форме или в форме
Шлемильха-Роша.
□
Обозначим
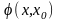 многочлен,
стоящий в (1), т.е.
многочлен,
стоящий в (1), т.е.
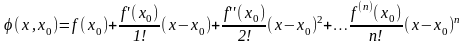
Тогда формула (1) имеет вид

или
 (3)
(3)
Ф ормула
Тейлора (1) будет доказана, если будет
установлено, что
определяется
по формуле (2).
ормула
Тейлора (1) будет доказана, если будет
установлено, что
определяется
по формуле (2).
Возьмем в окрестности точки некоторое число
и
рассмотрим отрезок
 .
Рассмотрим вспомогательную функцию
переменной t
.
Рассмотрим вспомогательную функцию
переменной t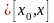 ,
которую получим из (3):
,
которую получим из (3):
 (4)
(4)
Эта функция
удовлетворяет условиям т. Ролля по
переменной t.
Она непрерывна и дифференцируема на
,
т.к.
дифференцируема
 раз. Вычислим значения на концах отрезка
.
раз. Вычислим значения на концах отрезка
.
Запишем
 подробнее:
подробнее:

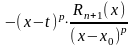 на
.
на
.
 ,
т.е.
,
т.е.

При
 имеем
имеем

 из формулы (3) по
определению
.
Т.е.
из формулы (3) по
определению
.
Т.е.
 .
Тогда по теореме Ролля
.
Тогда по теореме Ролля
 ,
что
,
что
 .
Найдем
.
Найдем
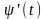 :
:


 .
.
Таким
образом
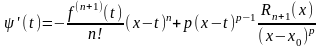 .
.


 .
.
 .
.
 .
.
Таким образом доказано, что остаточный член имеет вид (2), если имеет место формула (1). ■
Замечание
1. Ясно, что
аналогичное доказательство будет, если
 ,
т.е. если брать точку
слева от точки
.
,
т.е. если брать точку
слева от точки
.
Замечание
2. Если
 ,
то формула Тейлора называется формулой
Маклорена и имеет вид:
,
то формула Тейлора называется формулой
Маклорена и имеет вид:
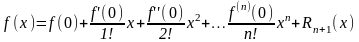 .
(5)
.
(5)
Замечание 3. Рассмотрим частный случай, разложение по формуле Тейлора алгебраического многочлена, т.е.
 .
.
Так
как
 , то
, то
 ,
и формула принимает вид:
,
и формула принимает вид:
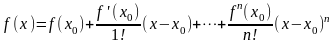 .
.
Здесь
-
любая точка вещественной прямой. Таким
образом, любой многочлен можно представить
как многочлен по степени
 ,
где
- любое число.
,
где
- любое число.
Замечание
4. Обозначим
 ,
,
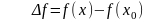 .
.
Тогда
 :
:
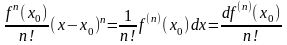 и формула Тейлора в дифференциальной
форме будет иметь вид:
и формула Тейлора в дифференциальной
форме будет иметь вид:

или
 .
.
Формула Тейлора выведена с остаточным членом в общей форме. Существуют и другие виды остаточного члена.
 Обозначим
Обозначим
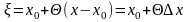 ,
,
 .
.
Положим
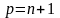 .
Тогда
.
Тогда
 .
.
или
 .
.
Такой вид остаточного члена называется остаточным членом в форме Лагранжа.
2) Положим
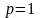 .
Тогда
.
Тогда
 ,
,
 .
.
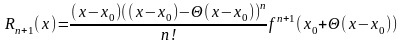 .
.
или
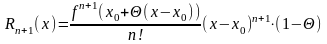 - остаточный
член в форме Коши.
- остаточный
член в форме Коши.
3) Пусть функция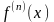 непрерывна в точке
,
следовательно функция
непрерывна в точке
,
следовательно функция
 также непрерывна в точке
,
т.к.
также непрерывна в точке
,
т.к.
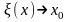 при
,
т.е.
при
,
т.е.
 при
.
Запишем формулу Тейлора с остаточным
членом
при
.
Запишем формулу Тейлора с остаточным
членом
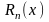 и
затем преобразуем её:
и
затем преобразуем её:
 .
.
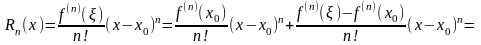
 .
.
 т.к.
т.к.
 при
.
при
.
Таким
образом

 .
.
Последнее слагаемое

называется остаточным членом в формуле Пеано. Итак
 .
.
Очевидно,
что разные формы остаточного члена
верны и при ,
т.е. при
,
т.е. при
 .
.
