Предельная точка, но не внутренняя
Предельная точка и внутренняя
Все точки интервала
- внутренние, а все точки
- изолированные
Определение 28.
Множество Х – называется замкнутым,
если оно содержит все свои предельные
точки
- замыкание
Определение 29.
Множество Х – называется открытым, если каждая его точка внутренняя
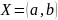- открытое
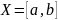- замкнутое
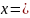- неоткрытое и незамкнутое
Теорема 9.
Если х – предельная точка множества Х,
то любая её
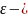окрестность содержит бесконечное число
точек множества Х
Доказательство: От противного.
Предположим, что
которая содержит конечное число точек
множества Х
Ясно, что расстояние между
Тогда
Это невозможно, так как х – предельная точка
§1.6 Комплексные числа
С – множество всех упорядоченных пар действительных чисел
Сумма двух упорядоченных пар
Произведение двух пар
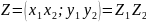
Назовем равным
Определение 30.
Множество с определенными на нем операциями «+» и «*» называется множество комплексных чисел
Частный случай
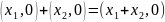
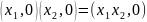
Получаем числа
такой же структуры, после умножения
комплексного числа
получаем число вида c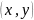
поэтому числа вида
- можно отожествить с вещественным
числом х
Таким образом,
все вещественные числа вложены в
множество комплексных чисел
Рассмотрим
Тогда
Мнимая
единица, тогда любое комплексное число
-
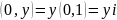
комплексное
число в алгебраической форме
X
- действительная часть числа
y
- мнимая часть
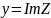
Для комплексных чисел имеют место свойства, что и для действительных чисел
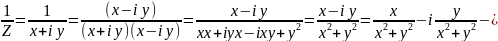
Обратное комплексное число
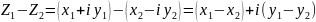
Таким образом,
отсюда ясно, что при выполнении
арифметических операций над комплексными
числами в алгебраической форме нужно
действовать по правилу с обычными
двучленами, учитывая, что
-
комплексно – сопряженное с числом Z
Для комплексно-сопряженных чисел свойства:
1)
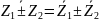
2)
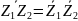
3)
На множестве комплексных чисел можно решать квадратные уравнения с отрицательным D
Основная теорема алгебры
Любой многочлен
имеет ровно n
корней, с учетом кратности
Прямоугольная система координат – декартова система, ОМ – является геометрической интерпретацией комплексного числа, ясно, что множество точек плоскости Оху и множество комплексных чисел – эквивалентны
- (длина вектора)
модуль
комплексного числа Z
Полярный угол
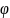- угол между положительным направлением
Ох и ОМ называется аргументом
числа Z
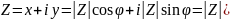
- комплексное
число в тригонометрической форме
Операции «*», «/» и возводить в степень и извлечение удобно проводить для комплексных чисел в тригонометрической форме
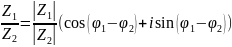
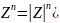Муавра
Доказательство:
