Тема 1.

1. Множества. Операции над множествами. Определение функции.

Множества – совокупность объектов, которые объединены в одну группу по некоторым признакам

Два множества называются равными – если они состоят из тех же элементов

Функцией F заданной на множестве Х и принимаемых значения на множестве У называется правилом по которому элементу стать в соответствие строго 1

2. Эквивалентные множества. Теоремы 1, 2, 3 о счетных множествах.

Определение 10. Множества А и В называются эквивалентными, если существуют взаимно-однозначные отображения этих множеств

Свойства:

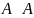1. - рефлексивность

2. - симметричность

3. - транзитивность (перенос через)

Определение 12. Множество А называется счетным, если А , если множество А можно занумеровать, в противном случае, множество А называется несчетным

Определение 13. Функция определенная на множестве F натуральных чисел, не принимающая значения из некоторого множества А, называется последовательностью

Теорема 1.

Всякое бесконечное подмножество В счетного множества А, тоже счетно

Доказательство:

Так как А – счетно, то между его элементами и элементами В можно установить взаимно-однозначные соответствия, то элементы А можно занумеровать

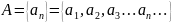
Пусть , имеющее натуральное число, что

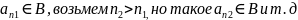
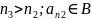
Рассмотрим

В – бесконечное множество, по условию теоремы и его элементы мы занумеровали, В , следовательно, установлено взаимно-однозначное соответствие элементов множества В и , и следовательно, множество В – счетное

Теорема 2.WHAT A FUCK?..o_O

Счетное объединение счетных множеств – счетное

Доказательство:

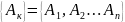
Счетное объединение счетных множеств (последовательность)

Докажем, что множество S счетное, так как каждый множество , то его элементы можно расположены в виде строки таблицы

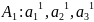
Бесконечна таблица вправо и вниз запишем элементы таблицы в виде последовательности, перечисляя их по направлению указанных стрелок 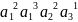каждый элемент таблицы устанавливает место в этой последовательности, следовательно, можно занумеровать, следовательно множество элементов таблицы счетно

Чтобы получилось множество S, нужно из этой последовательности выбросить элементы, которые уже встречались ранее, таким образом S – есть бесконечное подмножество счетного множества

3. Бесконечные десятичные дроби. Теорема 1 о нечетности бесконечных десятичных дробей.

Определение 14.

Бесконечной десятичной дробью называется последовательность цифр

Где - неотрицательное целое число, перед которым поставлен « - », а

Теорема 4.

Множество всех бесконечных дробей не счетно

Доказательство:

Докажем это утверждение для положительных дробей

Доказательство от противного.

Предположим множество А бесконечных десятичных дробей – счетно

Все положительные дроби могут быть занумерованы

указать десятичную дробь, коротая в этой последовательности, не содержится - число возьмем так,

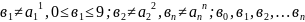
в множестве А по построению

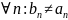
Это противоречие, а следовательно множество положительных десятичных дробей несчетно, а следовательно не счетно множество всех действительных чисел

4. Рациональные и действительные числа. Сравнение действительных чисел. Теоремы 2, 3 о множестве действительных чисел.

Определение. Рациональное число 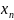заданное формулой 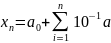называется нижним - значным приближением десятичной дроби Х