ВОПРОС 1. Основные понятия математической статистики.
ВОПРОС 2. Понятие выборки. Числовые характеристики выборки.
ВОПРОС 3. Измерение и измерительные шкалы (отношения и порядка).
ВОПРОС 4. Шкала отношений.
ВОПРОС 5. Шкала порядка. Правило ранжирования.
ВОПРОС 6. Типовые задачи анализа.
Можно выделить 3 типа задач:
Задачи описания данных (понимание и информирование результатов измеренных характеристик исследуемых объектов)
Установления совпадения характеристик двух групп (эксперим и контр)
Установления различий характеристик двух групп (эксп и контр)
|
Шк. ОТНОШ |
Шк. ПОРЯД |
описание |
1.1 |
1.2 |
уст. совпад. |
2.1 |
2.2 |
уст. различ. |
3.1 |
3.2 |
Итог: 6 задач, являющиеся базовыми по след. признакам:
1. они включают большинство задач, анализов данных в экспериментальных исследованиях по педаг. наукам.
2. они сформированы для простой схемы организ. пед. эксперимента – когда состояние исследуемых объектов описывается одним показателем. И измеряется два раза – до начала эксперимента и после его завершения.
Вопрос 7. Методы обработки данных выборки (описательная статистика, анализ совпадения и различий характеристик)
Вопрос 8. Статистические гипотезы. Общие принципы проверки статистических гипотез.
Вопрос 9. Статистические критерии. Алгоритм выбора статистического критерия.
Статистический критерий – строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости.
Виды:
1. критерий значимости (закон распределения – нулевая и альтернативная гипотезы)
2. критерий согласия (проверка предположения о том, что исследуемая случайная величина подчиняется предполагаемому закону)
3. проверка на однородность (подчиняются случайные величины одному и тому же закону)
Непараметрические критерии (которые не включают в расчет параметры вероятностного распределения т основаны на оперирование рангами): розенбаума, манна-уитни, уилкоксона.
Параметрические (включают в расчет вероятностное распределение признака – дисперсии и средние)
фишера.
Алгоритм выбора.
В первом приближении этот алгоритм реагируется по след. схеме:
Если данные получены в рез-те измерения в шкале отношения, то использ-ся критерий манна-уитни.
если в шкале порядка, то х2.
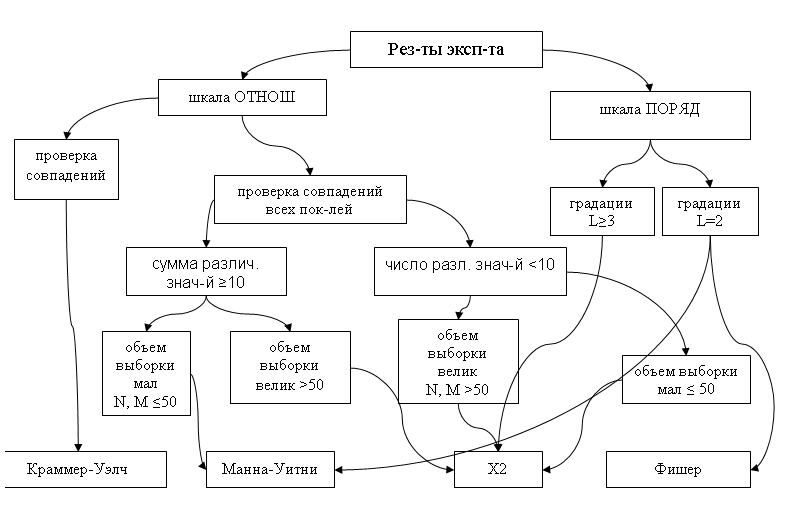
вычисл-ся эмп знач-е, котор. срав-ся с крит. знач-ем. Если эмп < крит –то совпадают с 0,05, если эмп > крит – то различаются с 95%.
Вопрос 10. Методика определения достоверности совпадения и различия для экспериментальных данных, измеренных в шкале отношений и шкале порядка.
Вопрос 11. T-критерий Краммера-Уэлча.
для данных, изм. в шкале отношения, позволяет устанавлить различия и совпадения м/у 2 выб-и.
Формула:
M-объем контр. гр.
N-объем эксп. гр.
^х-ср арифм эксп гр
^y-ср арифм контр гр
Dx-выбор.дисп.эксп.гр
Dy-выбор.дисп.контр.гр
Алгоритм:
- если Тэмп=<Т0,05 то совп. 0,05
- если Тэмп>Т0,05 то разл. 95%
Т0,05=1,96
Вопрос 12. W-критерий Вилкоксона-Манна-Уитни.
Изм-ся в шкале отношений.
Формула:
Алгоритм:
ВОПРОС 13. Критерий x^2.
по данным измер в шкале порядка, устанавливается различия между 2мя выб.
Формула:
M – объем контр.гр.
N – объем эксп.гр.
n1 – кол-во эксп.низ.б.
n2 – ср.б
n3 – выс.б
m1– контр.гр.низ.б.
m2 – ср.б.
m3 – выс.б.
Алгоритм:
Если Х2эмп>5,99 то разл с 95%
Если Х2эмп=<5,99 то совп с 0,05.
Вопрос 14. F-критерий Фишера.
Дихотомической шкалой наз-ют частный случай поряд. шкалы, содержащей 2 уровня: высокий ур-нь знаний и низкий, справился с заданием или нет и тд.
Достоверность совпадений и различий для данных, измеренных в ДШ мб установлена с помощью критерий Фишера.
Критич значение критерия:
F0,05 = 1,64
Формула:
M-объем 1 выб
N-объем 2 выб.
р-доля членов от общего числа 1 выб, получ макс. балл
q-доля членов от общ. числа 2 выб., получ. макс. балл.
Алгоритм: (опр-ся достоверность совпадений и различий для данных, измер в ДШ):
1. Если Fэмп =<1,64 то совпадают с ур-нем 0,05
2. если Fэмп > 1,64 то различаются с 95%
Вопрос 15. Q-критерий Розенбаума.
Данный признак используется для оценки различий между 2 выборками по уровням какого-либо признака, количественно измененного между двумя выборками. В каждой выборке должно быть не менее 11 испытуемых. Данный признак применяется ждя данных, изм. в шкале порядка. Данные могут быть упорядочены по возрастанию или убыванию исслед. признака и относит. знач-й, измер-х в этой шкале нельзя сказать, какое из них больше или меньше.
Ограничения критерия (применим, когда испытуемых больше 11):
1. если исп-х не меньше 11, не больше 50 – модуль разности между числом испытуемых 1 и 2 выб-ки не был больше 10 набл.
2. от 51 до 100 – модуль разности не больше 20.
3. больше 101, то одна из выборок должна отличаться от другой в 1,5 – 2 раза.
Алгоритм:
Упорядочить значения выборок в порядке убывания. За первую примем ту, чьи значения больше.
Во второй выборке определяем максим. эл-т и считаем кол-во эл-тов первой выборки, превыш. его. (S1) Определяем миним. эл-т первой выборки и считаем кол-во эл-тов 2 выборки, меньше него (S2)
Подсчитываем эмпирич. значение по формуле: Qэмп=S1+S2.
Выдвигаем гипотезы. (нулевая – 1 не превыш 2; альтернативная – 2 превышает 1)
По таблице крит. значений для случая число испытуемых в каждой из рассм. выборок не превышает 26. Определяем крит. значение критерия и обозначаем его через Q0,05 Если число превыш 26, то Q0,05=8
Если Qэмп >=Q0,05 то применяетмя альтернативная гипотеза.H1.
Критерии не применим, когда выборки имеют одинаковый разброс значений.