13. Дискретные по времени функции и разностные уравнения(Шидловский с.В. Сказал, что по этой теме скорее всего будет задавать вопросы Светлаков а.А.)

Дискретность (и следовательно, разрывность) сигналов обусловлена их квантованием по уровню и/или времени. В противоположность непрерывным функциям времени, дискретные сигналы могут принимать дискретные значения в дискретные моменты времени.

Дискретные сигналы во временной области представляют собой последовательность импульсов, появляющиеся в определённые моменты времени. Обычно дискретный сигнал получают в результате периодического прерывания непрерывного сигнала с постоянным тактом. Существуют разные способы модуляции отдельных импульсов входящих в последовательность. Они отличаются допустимыми значениями амплитуд, шириной импульсов и модулирующей частотой. В цифровых системах управления обычно применяется лишь ампл. модуляция. Причем в том её варианте, при котором высота импульса пропорциональна текущему значению непрерывного сигнала, ширина постоянна, а интервалы между импульсами одинаковы и равны такту квантования.

Дискретный сигнал – сигнал дискретный по времени, но не квантованный по уровню.

Сигнал, дискретный по времени и квантованный по уровню – цифровой сигнал.

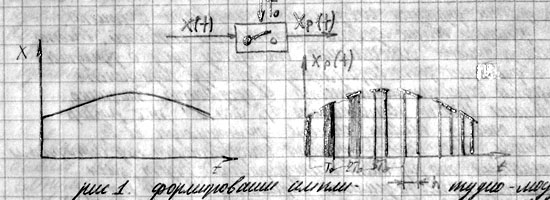
Формирование амплитудно-модулированного дискретного сигнала путем пропускания непрерывного сигнала через ключ с периодом квантования T₀.

Поскольку к дискретным сигналам применим принцип суперпозиции, они описываются линейными соотношениями аналогичными по форме уравнениям линейных динамических систем

Xт=X(kT), при t=kT₀

Xт=0 при kT₀ < t < (k+1)T₀ k=1,2,3…

Разностные уравнения 

Аналогом дифференциальных уравнений для импульсной системы является уравнение в конечных разностях или разностное уравнение (РУ). При использовании прямых разностей неоднородные лин. разностные уравнения имеют вид:

(здесь все дельты вот такие ∆)

f[n]- заданная, а y[n]-искомая решетчатые функции. При f[n]Ξ 0 уравнение становится однородным разностным уравнением, решением которого будет y[n].

Так же его можно представить в другом виде:

a₀y[n+m] + a₁y[n+m-1] +…+ a_my[n] = f[n] (1)

При использовании обратных разностей уравнение в конечных разностях будет:

Либо в другом виде:

a₀y[n] + a₁y[n-1] +…+ a_my[n-m] = f[n] (2)

Разностные уравнения можно рассматривать как рекуррентные соотношения, позволяющие вычислять значения 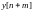при для заданных начальных значений y[0], y[1], …, y[m-1] и уравнения вида (1) или значения y[n] при n=0,1,2… для заданных начальных значений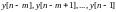 и уравнения вида (2).

Общее решение однородного разностного уравнения: , где z – корни характеристического уравнения a₀z^m+a₁z^m-1+…+a_m= 0, а C_i- произвольные постоянные.

13. Z-преобразование

Математическое описание и анализ импульсной системы с амплитудной модуляцией существенно упрощается, если все сигналы в системе (как в импульсной, так и в непрерывной) рассматриваются только в дискретные моменты времени . При этом каждый непрерывный сигнал x(t) удобно представлять в виде решетчатой функции времени x(kT), значения которой определяемы только для дискретных моментов времени.

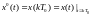(у x вместо 0 должна быть*)

Между дискретными значениями аргумента t функция 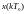равна нулю. Непрерывная функция x(t) является огибающей для решетчатой функции , и каждому конкретному сигналу x(t) соответствует вполне определенный сигнал . Часто удобнее переходить к относительному времени (тождественно равно), измерять время числом периодов квантования. В этом случае относительный период , а решетчатая функция обозначается x(k).

П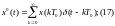 оследовательность неединичных импульсов, образующих решетчатую функцию на интервале , можно представить в виде бесконечного ряда (т.е. последовательности идеальных импульсов).

(у икса вместо 0 должна быть *)

где - смещенная дельта-функция(«идеальные» импульсы), существующая только в моменты времени 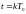и равная нули при всех других значениях t.

П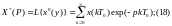 рименяя к сумме (17) преобразование Лапласа с учетом, что изображение суммы оригиналов равно сумме их изображений, а так же, что согласно теореме запаздывания, изображение смещенной дельта-функции равно exp(-p/kT₀), тогда изображение решетчатой функции (17) по Лапласу:

Выражение (18) – дискретное преобразование Лапласа. С целью получения передаточный функций импульсных систем в дробно-рациональной форме, свойственной непрерывным системам, целесообразна замена аргументов

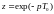, и тогда

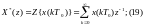И тогда вместо (18) получают более удобное преобразование:

19 – z-преобразование решетчатой функции.

Смысл заключается в том, что в последовательности чисел ставится в соответствие функция комплексной переменной z, определяемая выражением (19). X(z) определена только для тех значений z, для которых ряд (19) сходится.

Z-преобразование играет для дискретных сигналов такую же роль, как и преобразование Лапласа для аналоговых. Определяющим при этом является тот фактор, что z-преобразование импульсной характеристики дискретной системы является дробно-рациональной функцией переменной z.

Главное достоинство – простота выполнения прямого и обратного преобразования:

1 – чтобы по известной функции времени x(t) найти ее z-преобразование, необходимо лишь каждое дискретное значение x(kT₀) умножить на z^-k, а затем свернуть степенной ряд в конечную сумму;

2 – чтобы по известному изображению X(z) найти соответствующий сигнал x(t), необходимо представить изображение X(z) в виде степенного ряда по убывающим степеням z^-k, получившееся при это числовые коэффициенты ряда и есть дискретные значения x(kT₀) сигнала x(t).