Временные характеристики
Динамические свойства звена могут быть определены по его переходной функции и функции веса.
Переходная функция, или переходная характеристика, h (t ) представляет собой переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис. 13). Такое входное воздействие называется единичной ступенчатой функцией и обозначается x1(t ) = 1(t ), что соответствует х1 = 0 при t < 0 и x1 = 1 при t > 0. Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.
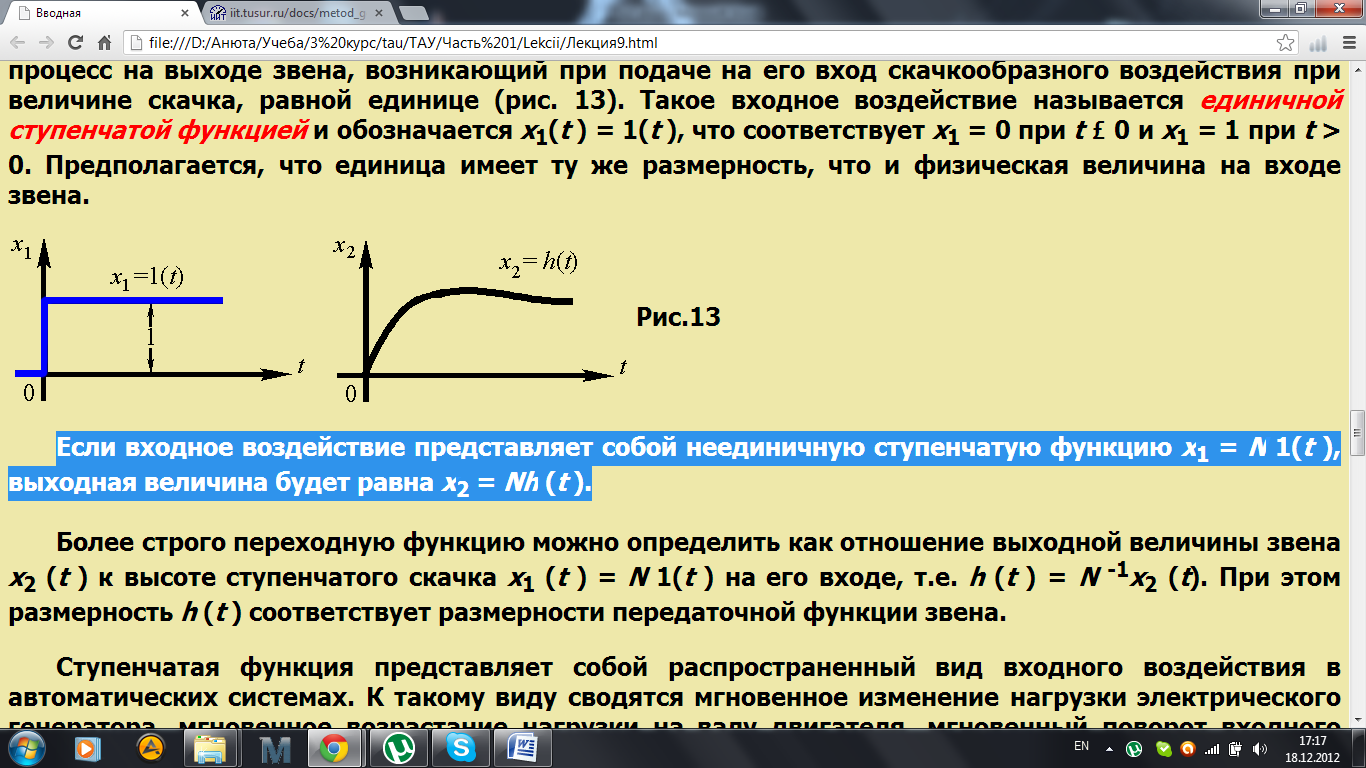
Если входное воздействие представляет собой неединичную ступенчатую функцию x1 = N 1(t ), выходная величина будет равна х2 = Nh (t ).
Умножение какой-либо функции времени х (t ) на единичную ступенчатую функцию 1(t ) означает, что функция времени х (t ) будет существовать только при t > 0, при t < 0 она обращается в нуль. Это иллюстрируется рис. 14.
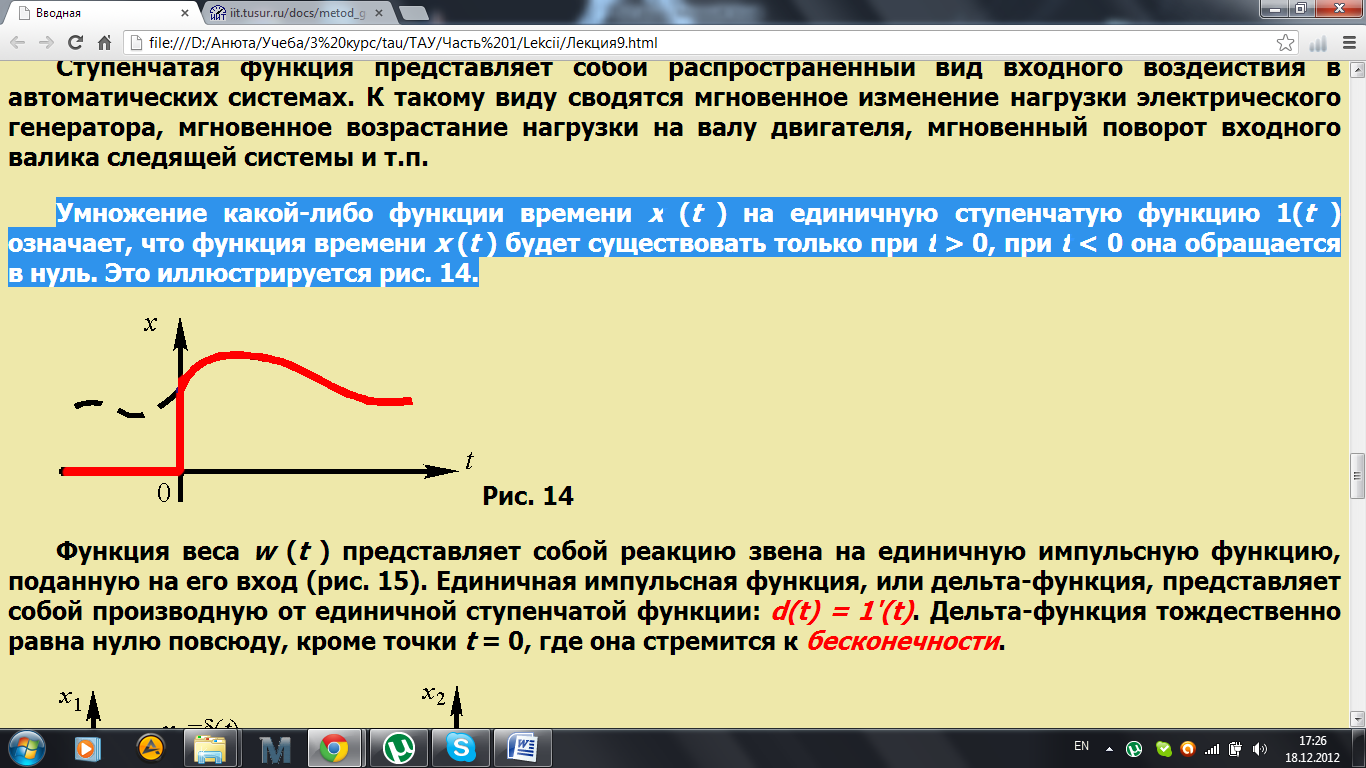
Функция веса w (t ) представляет собой реакцию звена на единичную импульсную функцию, поданную на его вход (рис. 15). Единичная импульсная функция, или дельта-функция, представляет собой производную от единичной ступенчатой функции: d(t) = 1'(t). Дельта-функция тождественно равна нулю повсюду, кроме точки t = 0, где она стремится к бесконечности.
Функция веса может быть получена дифференцированием по времени переходной функции.
В случае, если на вход звена поступает неединичная импульсная функция x1 = G d(t), на выходе звена получится x2 = Gw (t).
Частотная передаточная функция и частотные характеристики
Частотная передаточная функция W (j w) представляет собой комплексное число, модуль которого равен отношению амплитуды выходной величины к амплитуде входной, а аргумент - сдвигу фаз выходной величины по отношению к входной:
Частотную передаточную функцию можно легко получить из обычной передаточной функции подстановкой p=jw:
W(jw)=x2(jw)/x1(jw)= W(p)
Частотная передаточная функция может быть представлена в следующем виде:
W(jw)= A(w)exp(jᴪ(w)) = Re(w) + j*Im(w)
A(w) – АЧХ, ᴪ(w) – ФЧХ, Re(w) – ВЧХ, Im(w) – МЧХ.
АЧХ показывает, как пропускает звено сигнал различной частоты. ФЧХ показывает фазовые сдвиги, выносимые звеном на различных частотах.
Можно построить также вещественную и мнимую частотные характеристики по функциям Re(w) и Im(w). Вещественная характеристика представляет собой четную функцию частоты, а мнимая характеристика - нечетную функцию частоты.
Амплитудно-фазовая частотная характеристика (а.ф.х.) строится на комплексной плоскости. Она представляет собой геометрическое место концов векторов (годограф), соответствующих частотной передаточной функции W (j w) = U (w) + jV (w) при изменении частоты от нуля до бесконечности (рис. 17). По оси абсцисс откладывается вещественная часть U (w) = Re W(jw) и по оси ординат - мнимая часть V(w) = Im W(jw). Для каждой частоты на комплексной плоскости наносится точка. Полученные точки соединяются затем плавной кривой. Около нанесенных точек можно написать соответствующие им частоты w1, w2, w3 и т.д.
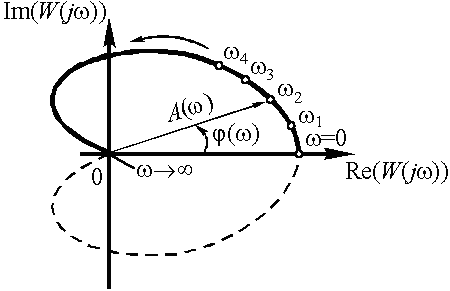
Связь между различными видами частотных характеристик следующая
;
;
;
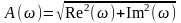
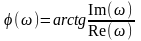