1. Способы описания динамических элементов аср

Работу АСР можно описать словесно, такое описание помогает понять принцип действия системы, ее назначение, особенности функционирования и др. Однако, этот способ не является универсальным, и, что самое главное, не дает количественной оценки характеристикам системы и ее качеству регулирования.

При создании САУ одной из первоочередных задач является математическое описание системы. Математическое описание сопровождается разбиением системы на звенья и описанием этих звеньев. Совокупность уравнений отдельных звеньев определяет уравнение системы в целом. Основу математического описания САУ составляет структурная схема. Звенья изображаются прямоугольниками, их входы и выходы соединяются стрелками, которые показывают связи между звеньями и внешние воздействия, приложенные к отдельным звеньям системы. Внутри прямоугольника записывается уравнение или характеристика, описывающие звено.

Уравнения звеньев обычно записываются через переменные состояния x(t) в нормальной форме, в виде системы дифференциальных уравнений 1го порядка, разрешенных относительно первых производных:

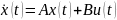или

2. Уравнения систем автоматического регулирования

Обычно дифференциальные уравнения системы записывают в таком виде, где значения регулируемой величины и ее производных располагаются в левой части уравнения. Значения входных воздействий (управляющих и возмущающих) и их производных располагаются в правой части. При это уравнение САУ примет вид:

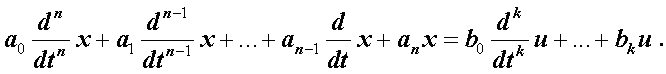
или (a₀pⁿ+a₁p^n-1+…+a_n)x = (b₀p^m+b₁p^m-1+…+b_m)u

Первая стандартная символическая форма записи лин. диф. уравнения имеет вид:

(T₂²p² + T₁p + 1)y = k(Tp + 1)x,

где T₁ = a₁/a₂; T₂² = a₀/a₂; T = b₀/b₁; k = b₁/a₂ (размерность b₁/ размерность a₂ )

Т – постоянные времени звена, измеряющиеся в секундах, характеризуют инерционность звена; k – передаточный коэффициент звена.

Вторая стандартная символическая форма записидиф. уравнения через передаточную функцию звена:

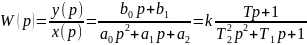
где W(p) характеризует отношение изображений (по Лапласу) выходной величины звена к входной при нулевых начальных условиях и равенстве нулю всех внешних возмущений.

Третья стандартная форма записи диф. уравнения применяется относительно переменных состояния, когда САУ описывается векторно-матричным диф. уравнением:

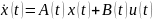
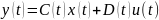
А – квадратная матрица коэффициентов 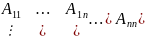; B – матрица управления (B₁₁ – B_nm); C – матрица выхода (С₁₁-С_ln); D – матрица обхода системы (D₁₁-D_lm); u – m-мерный вектор входных переменных (управляющих и возмущающих); x – n-мерный вектор переменных состояния координат, полностью характеризующих состояние системы; y – l-мерный вектор наблюдаемых или выходных переменных.

Если САУ описана в виде уравнений типа вход-выход, то возможен переход к уравнениям состояния и наоборот.

3. Передаточные функции

Передаточной функцией линейного стационарного динамического элемента (системы) называется отношение преобразования Лапласа выходного сигнала (регулируемого) к преобразованию Лапласа входного сигнала (заданного) при нулевых начальных условиях.

W(p)=Y(p)/X(p)

(1)

Однако такая запись (1) неудобна, удобнее будет записывать связь между входом u и выходом x посредством некоторого оператора, осуществляющего операцию над входной величиной u, чтобы получить выходную величину x. Дли этого m-ю производную d ^m x/dt ^m  формально заменим величиной p ^m x (m = 0,1,2,...); при этом p ⁰ = 1 означает отсутствие дифференцирования. Тогда выражение (1) можно переписать в виде

или

Обозначим

Таким образом, функция W (p ) равна отношению двух полиномов

Уравнение является характеристическим уравнением дифференциального уравнения (1), а поэтому оно также называется характеристическим уравнением звена, а сам полином D (p ) называется характеристическим полиномом звена.