Фундаментальная система решений.
Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений. Однородные системы
Однородной системой линейных уравнений называется система вида:
Нулевое решение системы (1) называется тривиальным решением.
Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.
Если существует любое ненулевое решение системы, то оно называется нетривиальным.
Векторы на плоскости и пространстве.
Векторные поля на плоскости
Если 
— радиус-вектор,
который в заданной системе координат
имеет вид 
,
то векторное поле описывается вектор-функцией вида:
N- мерный вектор и векторное пространство.
В случае
ортогональной системы векторов 
имеет
место равенство, которое тоже называют
теоремой Пифагора:
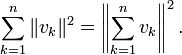
Если — это проекции вектора на координатные оси, то эта формула совпадает с расстоянием Евклида — и означает, что длина вектора равна корню квадратному суммы квадратов его компонентов.
Аналог этого равенства в случае бесконечной системы векторов имеет название равенства Парсеваля.
Размерность и базис векторного пространства.
Ве́кторное (лине́йное) простра́нство — основной объект изучения линейной алгебры.
Определение
Линейное,
или векторное пространство 
над полем 
—
это непустое
множество 
,
на котором введены операции
сложения,
то есть каждой паре элементов
множества 
ставится
в соответствие элемент того же множества,
обозначаемый 
и
умножения
на скаляр (то
есть элемент поля
),
то есть любому элементу 
и
любому элементу 
ставится
в соответствие единственный элемент
из
,
обозначаемый 
.
При этом на операции накладываются следующие условия:
,
для любых
(коммутативность
сложения);
,
для любых 
(ассоциативность
сложения);
существует
такой элемент 
,
что 
для
любого
(существование
нейтрального элемента относительно
сложения), в частности
не
пусто;
для
любого
существует
такой элемент 
,
что 
(существование
противоположного элемента относительно
сложения).
(ассоциативность
умножения на скаляр);
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Элементы множества называют векторами, а элементы поля — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
Переход к новому базису.
Базис и разложение по базису
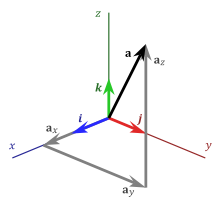
Разложение вектора по трём ортогональным векторам трёхмерного евклидова пространства
Векторы (как направленные отрезки), лежащие на прямых, параллельных одной прямой, называются коллинеарными, а векторы, лежащие в плоскостях, параллельных одной плоскости — компланарными. Для свободных векторов коллинеарность и компланарность определяется как такие понятия для изображающих их направленных отрезков (то есть представителей соответствующих свободным векторам классов эквивалентности).
Каждый вектор плоскости можно единственным образом разложить по двум определённым неколлинеарным векторам этой плоскости, а каждый вектор трёхмерного евклидова пространства можно единственным образом разложить по трём определённым некомпланарным векторам. Эти векторы, взятые в определённом порядке называются базисом плоскости (пространства). Сопоставлением каждому вектору данной плоскости (пространства) его коэффициентов в таком его разложении, определяется аффинная система координат на плоскости (в пространстве). Если векторы, по которым производится разложение, ортогональны и единичны, то получаем прямоугольную декартову систему координат на плоскости (в пространстве). Разложение геометрического вектора по базису есть упорядоченная совокупность проекций вектора на базисные вектора.
[править]Обозначения
Вектор,
представленный набором
элементов
(компонент) 
допустимо
обозначить следующим способами:
.
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
Сложение векторов почти всегда обозначается знаком плюс:
.
Умножение на число — просто написанием рядом, без специального знака, например:
,
причём число при этом обычно пишут слева.
Умножение на матрицу также обозначают написанием рядом, без специального знака, но здесь перестановка сомножителей в общем случае влияет на результат. Действие линейного оператора на вектор также обозначается написанием оператора слева, без специального знака.
Евклидово пространство.
Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В
современном понимании, в более общем
смысле, может обозначать один из сходных
и тесно связанных объектов, определённых
ниже. Обычно
-мерное
евклидово пространство обозначается 
,
хотя часто используется не вполне
приемлемое обозначение 
.
1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство с введённым на нём (положительно определенным) скалярным произведением, порождающим норму:
,
в простейшем случае (евклидова норма):
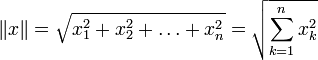
где 
(в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
2. Метрическое пространство, соответствующее пространству описанному выше. То есть с метрикой, введённой по формуле:
,
где
и 
.
Связанные определения
Под евклидовой метрикой может пониматься метрика, описанная выше, а также соответствующая риманова метрика.
Под локальной евклидовостью обычно имеют в виду то, что каждое касательное пространство риманова многообразия есть евклидово пространство со всеми вытекающими свойствами, например, возможностью (по гладкости метрики) ввести в малой окрестности точки координаты, в которых расстояние выражается (с точностью до какого-то порядка) в соответствии с описанным выше.
Метрическое пространство называют локально евклидовым также если возможно ввести на нём координаты, в которых метрика будет евклидовой (в смысле второго определения) всюду (или хотя бы на конечной области) — каковым, например, является риманово многообразие нулевой кривизны.