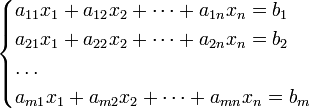10. Теорема о ранге матрицы.

Свойства

Теорема (о базисном миноре): Пусть   — базисный минор матрицы  , тогда:

базисные строки и базисные столбцы линейно независимы;

любая строка (столбец) матрицы   есть линейная комбинация базисных строк (столбцов).

Следствия:

Если ранг матрицы равен  , то любые   строк или столбцов этой матрицы будут линейно зависимы.

Если   — квадратная матрица, и  , то строки и столбцы этой матрицы линейно зависимы.

Пусть  , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно  .

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение   для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если  , то их ранги равны.

Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:

Количество главных переменных системы равно рангу системы.

Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

11. Понятие линейной зависимости (независимости) строк матрицы.

линейной зависимости 

Рассмотрим случай, когда в результате изучения зависимости некоторой скалярной величины   от некоторой скалярной величины   (Это может быть, например, зависимость напряжения   от силы тока  :  , где   — постоянная величина, сопротивлениепроводника) было проведено   измерений этих величин, в результате которых были получены значения   и соответствующие им значения  . Данные измерений должны быть записаны в таблице.

Таблица. Результаты измерений.

№ измерения
1
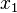
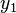
2
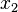
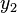
3
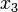
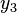
4
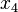
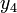
5
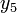
6

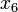
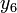
Вопрос звучит так: какое значение коэффициента   можно подобрать, чтобы наилучшим образом описать зависимость  ? Согласно МНК это значение должно быть таким, чтобы сумма квадратов отклонений величин   от величин 

была минимальной

Сумма квадратов отклонений имеет один экстремум — минимум, что позволяет нам использовать эту формулу. Найдём из этой формулы значение коэффициента  . Для этого преобразуем её левую часть следующим образом:

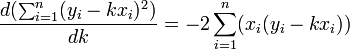
Далее идёт ряд математических преобразований:

Последняя формула позволяет нам найти значение коэффициента  , что и требовалось в задаче.

12. Системы m- линейных уравнений с n- переменными. Основные понятия и определения. Теорема Кронекера-Капелли.

Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида

Система линейных уравнений от трёх переменных определяет наборплоскостей. Точка пересечения является решением.

Здесь   — количество уравнений, а   — количество неизвестных. x1, x2, …, xn — неизвестные, которые надо определить. a11, a12, …, amn — коэффициенты системы — и b1, b2, … bm — свободные члены — предполагаются известными[1]. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно[2].

Система (1) называется однородной, если все её свободные члены равны нулю (b1 = b2 = … = bm = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Решение системы (1) — совокупность n чисел c1, c2, …, cn, таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения в тождества.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c1(1), c2(1), …, cn(1) и c1(2), c2(2), …, cn(2) совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c1(1) = c1(2), c2(1) = c2(2), …, cn(1) = cn(2).

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Доказательство (условия совместности системы)

[править]Необходимость

Пусть система совместна. Тогда существуют числа   такие, что  . Следовательно, столбец   является линейной комбинацией столбцов   матрицы  . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что  .

[править]Достаточность

Пусть  . Возьмем в матрице   какой-нибудь базисный минор. Так как  , то он же и будет базисным минором и матрицы  . Тогда согласно теореме о базисном миноре последний столбец матрицы   будет линейной комбинацией базисных столбцов, то есть столбцов матрицы  . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы  .

[править]Следствия

Количество главных переменных системы равно рангу системы.

Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.

13. Методы решений системы N- линейных уравнений с n- переменными.

Однородной системой линейных уравнений называется система вида:

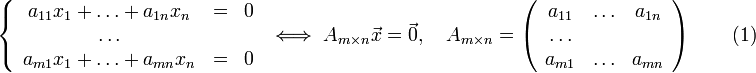
Нулевое решение   системы (1) называется тривиальным решением.

Однородные системы всегда совместны, т.к. всегда существует тривиальное решение.

Если существует любое ненулевое решение системы, то оно называется нетривиальным.

14. Метод обратной матрицы.

Обра́тная ма́трица — такая матрица A−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы

, где   обозначает определитель.

 для любых двух обратимых матриц   и  .

 где   обозначает транспонированную матрицу.

 для любого коэффициента   .

Если необходимо решить систему линейных уравнений  , (b — ненулевой вектор) где   — искомый вектор, и если   существует, то  . В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.