Алгебра

1. Основные алгебраические данные. Множества. Отношения.

Множество — одно из ключевых понятий математики, в частности, теории множеств и логики.

Понятие множества обычно принимается за одно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит, и не имеющее определения.

2. Бинарные операции.

Типы бинарных операций: Коммутативная операция

Бинарная операция   называется коммутативной, если её результат не зависит от перестановки операндов, то есть

Ассоциативная операция

Основная статья: Ассоциативная операция

Бинарная операция   называется ассоциативной, если

Альтернативная операция

Бинарная операция   называется альтернати́вной если

 и 

Примерами бинарных операций могут служить сложение, умножение и вычитание на поле вещественных чисел. Сложение и умножение чисел являются коммутативными и ассоциативными операциями, а вычитание — нет.

3. Кольца. Тела. Поля.

В абстрактной алгебре кольцо́ — это один из наиболее часто встречающихся видов алгебраической структуры.

Кольцо — это множество R, на котором заданы две бинарные операции: + и × (называемые сложение и умножение), со следующими свойствами:

 — коммутативность сложения;

 — ассоциативность сложения;

 — существование нейтрального элемента относительно сложения;

 — существование противоположного элемента относительно сложения;

 — ассоциативность умножения (некоторые авторы не требуют выполнения этой аксиомы[1])

 — дистрибутивность.

Те́ло — множество с двумя операциями (сложение и умножение), обладающее следующими свойствами:

Абелева группа относительно сложения.

Все ненулевые элементы образуют группу относительно умножения.

Дистрибутивность умножения относительно сложения.

По́лем называется множество F с двумя бинарными операциями   (аддитивная операция, или сложение) и   (мультипликативная операция, или умножение), если оно (вместе с этими операциями) образует коммутативное ассоциативное кольцо c единицей  , все ненулевые элементы которого обратимы.

4. Основные сведенья о матрицы.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.

5. Операции над матрицами и их свойства.

Операции над матрицами

Умножение матрицы на число

Умножение матрицы   на число   (обозначение:  ) заключается в построении матрицы  , элементы которой получены путём умножения каждого элемента матрицы   на это число, то есть каждый элемент матрицы   равен

Свойства умножения матриц на число:

1. 1A = A;

2. (λβ)A = λ(βA)

3. (λ+β)A = λA + βA

4. λ(A+B) = λA + λB

[править]Сложение матриц

Сложение матриц   есть операция нахождения матрицы  , все элементы которой равны попарной сумме всех соответствующих элементов матриц   и  , то есть каждый элемент матрицы   равен

Свойства сложения матриц:

1.коммутативность: A+B = B+A;

2.ассоциативность: (A+B)+C =A+(B+C);

3.сложение с нулевой матрицей: A + Θ = A;

4.существование противоположной матрицы: A + (-A) = Θ;

Все свойства линейных операций повторяют аксиомы линейного пространства и поэтому справедлива теорема:

Множество всех матриц одинаковых размеров mxn с элементами из поля P (поля всех действительных или комплексных чисел) образуют линейное пространство над полем P (каждая такая матрица является вектором этого пространства). Впрочем, прежде всего во избежание терминологической путаницы, матрицы в обычных контекстах избегают без необходимости (которой нет в наиболее обычных стандартных применениях) и четкого уточнения употребления термина называть векторами.

[править]Умножение матриц

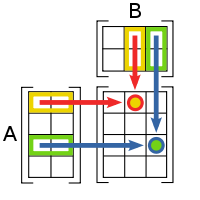
Умножение матриц (обозначение:  , реже со знаком умножения  ) — есть операция вычисления матрицы  , каждый элемент которой равен сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

Количество столбцов в матрице   должно совпадать с количеством строк в матрице  , иными словами, матрица   обязана быть согласованной с матрицей  . Если матрица   имеет размерность  ,   —  , то размерность их произведения   есть  .

Свойства умножения матриц:

1.ассоциативность (AB)C = A(BC);

2.некоммутативность (в общем случае): AB   BA;

3.произведение коммутативно в случае умножения с единичной матрицей: AI = IA;

4.дистрибутивность: (A+B)C = AC + BC, A(B+C) = AB + AC;

5.ассоциативность и коммутативность относительно умножения на число: (λA)B = λ(AB) = A(λB);

[править]Умножение вектора на матрицу

По обычным правилам матричного умножения осуществляется умножение на матрицу слева вектора-столбца, а также умножение вектора-строки на матрицу справа. Поскольку элементы вектора-столбца или вектора-строки можно записать (что обычно и делается), используя один, а не два индекса, это умножение можно записать так:

для вектора-столбца v (получая новый вектор-столбец Av):

для вектора-строки s (получая новый вектор-строку sA):

Вектор-строка, матрица и вектор столбец могут быть умножены друг на друга, давая число (скаляр):

6. Определители квадратных матриц.

Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (то есть такой, у которой количество строк и столбцов равно). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца. Определитель матрицы А обозначается как: det(A), |А| или Δ(A). Определение через разложение по первой строке

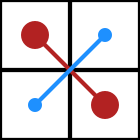
Схема расчета определителя матрицы   .

Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:

Для матрицы   детерминант определяется как

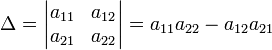
Для матрицы   определитель задаётся рекурсивно:

,    где   — дополнительный минор к элементу  . Эта формула называется разложением по строке.

В частности, формула вычисления определителя матрицы   такова:

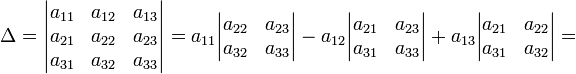
Легко доказать, что при транспонировании определитель матрицы не изменяется (иными словами, аналогичное разложение по первому столбцу также справедливо, то есть даёт такой же результат, как и разложение по первой строке):