14.2 Расстояние от точки до плоскости.

Пусть плоскость P задана в декартовых координатах общим уравнением

Ax+By + Сz + D = 0. Найдем расстояние d от точки М₀ до плоскости Р. Опустим из М₀ перпендикуляр на плоскость P, и пусть точка — основание этого перпендикуляра. Как и в случае определения расстояния от точки до прямой на плоскости, получаем, что

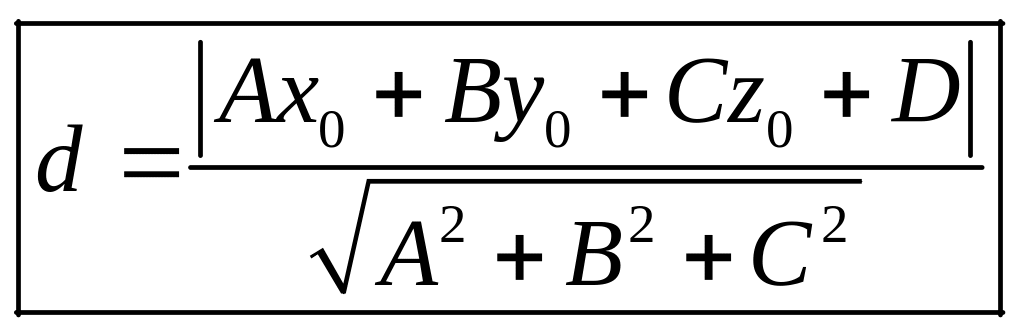(14.8)

14.3 Взаимное расположение двух плоскостей.

Две пересекающиеся плоскости образуют две пары вертикальных двугранных углов. Достаточно найти один из этих углов, тогда остальные углы определяются одно­значно.

Пусть плоскости и заданы общими уравнениями

:

:

Возможны следующие случаи взаимного расположения плоскостей:

а) Плоскости пересекаются и имеют общую прямую. В этом случае ранг матрицы

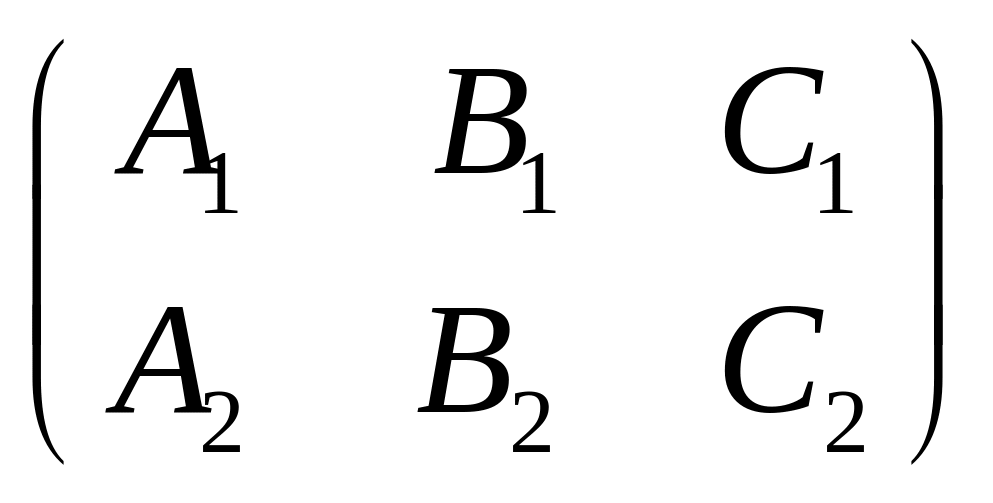равен двум, так как векторы

не коллинеарны.

б) Плоскости совпадают. В этом случае уравнения и равносильны,

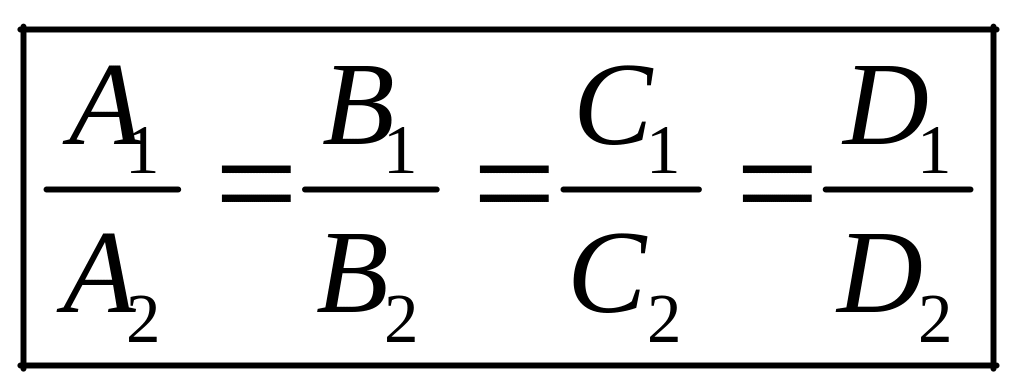- условие совпадения плоскостей, (14.9)

в) Плоскости параллельны. В этом случае векторы и коллинеарны и и

различные, т. е. уравнения плоскостей и не равносильные

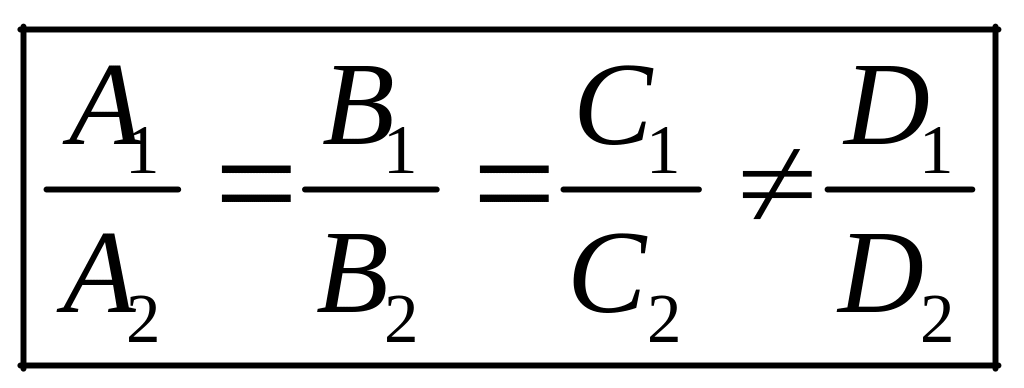- условие параллельности плоскостей. (14.10)

Найдем угол между плоскостями. Через произвольную точ­ку К на линии l пересечения плоскостей проведем пло­скость Q, перпендикуляр­ную прямой l . Линии пересечения пло­скости Q с плоскостями и определяют плоские углы, величинами которых измеряются двугранные углы. От точки K отложим нормали , плоскостей и . Эти нормали лежат в плоскости Q. Угол между векторами и (рис.14.3) равен одному из указанных линей­ных углов (по теореме об углах со взаимно перпендикулярными сторонами).

	Рис.14.3

Имеем

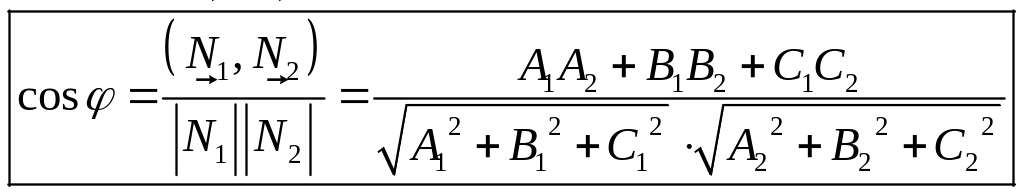(14.11)

Необходимым и достаточным условием перпендикулярности плоскостей и является перпендику­лярность векторов и , т. е. равенство

. (14.12)

14.4. Полупространство.

Всякая плоскость определяет два полупространства, общей границей которых она является. Пусть плоскость P (рис. 14.4) задана общим уравнением: Ax+By + Сz + D = 0.

	рис. 14.4

Через обозначим то полупространство с границей

Р, в которое направлен нормальный вектор , отложенный от произвольной точки плоскости Р. Другое полупространство с границей P обозначим через . Координаты точки обозначим через .

Для того чтобы произвольная точка М (x, у, z) принадлежала полупространству , необходимо и достаточно, чтобы < ; условие равносильно тому, что . Выражая скалярное произведение через координаты сомножителей, получим неравенство

. (14.13) Так как точка P, то ее координаты удовлетворяют уравнению плоскости. Поэтому

(14.14) Из последнего равенства и неравенства (14.13) получим неравенство Ax + By + Сz + D 0, задающее полупространство . Аналогично получим неравенство, задающее полупростран­ство : Ax+ By + Cz + D 0.

Легко видеть, что каждое из открытых полупространств, ограниченных плоскостью Р, задается одним из неравенств: Ах + By + C + D > 0, Ах + By + Сz + D < 0.