13.4 Уравнение отрезка

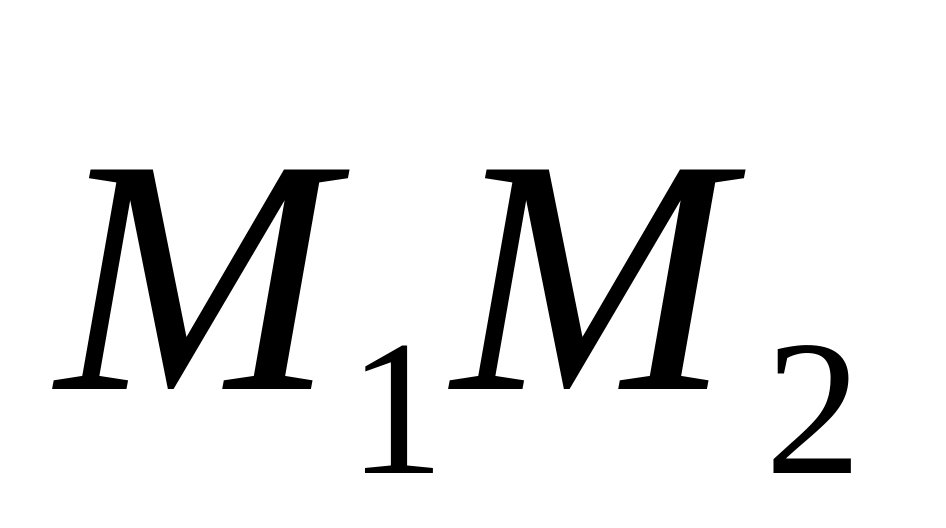Найдем уравнение прямой l, проходящей через точки и . Так как вектор параллелен прямой l, то ее параметрическое уравне­ние в векторной форме имеет вид

, .

Рис. 13.2

При t = 0 точка М совпадает с точкой . При увеличении параме­тра t точка М перемещается по прямой l от точки , к точке , а при t — 1 точка М совпадает с точкой

(рис. 13.2). Поэтому уравнение , , является параметрическим уравнением отрезка [ ] в векторной форме.

Так как = - , то уравнение отрезка можно записать в следующем виде

(13.14)

Пусть точки M, и имеют соответственно координаты (x, у), ( ) и ( ). Тогда

= ; = .

Из векторного равенства следует, что соответствующие координаты векторов и равны, т. е.

(13.15)

Эта система называется параметрическим уравнением отрезка.