Геометрия Л.06 стр. 6 09.03.25

Лекция 13

Цель лекции - изложение начал аналитической геометрии.

Тема 13. Геометрические образы на плоскости и в пространстве

13.1. Уравнение фигуры на плоскости

Геометрической фигурой или просто фигурой на плоскости будем называть множество точек на плоскости. Задать фигуру — значит ука­зать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравне­ний с двумя неизвестными. Произвольное уравнение с двумя неизвест­ными x и y будем записывать в виде F(x, у) = 0.

Выберем на плоскости некоторую прямоугольную систему коорди­нат. В этой системе координат уравнение F(x, у) = 0 называется урав­нением фигуры при выполнении следующих двух условий:

1) если точка M(а,b) принадлежит фигуре , то координаты (а,b) точки М являются решением уравнения F(x, у) = 0, т. е. F(a, b) = 0 — верное числовое равенство;

2) если же пара чисел (с, d) является решением уравнения F(x,у) = 0, то точка N, координатами которой служат числа c и d, принадлежит фи­гуре .

Из определения уравнения фигуры следует, что фигура состоит только из тех точек плоскости, координаты которых являются решени­ями уравнения F(x,у) = 0, т. е. уравнение фигуры задает эту фигуру.

Возможны два вида задач:

1) дано уравнение F(x, у) = 0, и надо построить фигуру , уравне­нием которой является F(x, у) = 0;

2) дана фигура , и надо найти уравнение этой фигуры.

Первая задача сводится к построению графика уравнения F(x, у) = 0 и решается чаще всего методами математического анализа.

Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:

1) задать фигуру геометрически, т. е. сформулировать условие, кото­рому удовлетворяют только точки фигуры (довольно часто определе­ние фигуры содержит такое условие);

2) записать в координатах условие, сформулированное в первом пункте.

Пример.1. Окружность Ф с центром в точке О и радиусом R задается условием M Ф , где — расстояние между точками O и М. Запишем это условие в координатах. Пусть центр O окружности имеет координаты (а,b), а через (x,у) обозначим координаты произ­вольной точки. Тогда условие в координатах имеет вид = .

Последнее уравнение, называется каноническим уравнением окружности с центром в точке O(а, b) и радиусом R.

13.2. Уравнения прямой на плоскости

Основная цель этого параграфа - доказать, что прямая на плоскости в декартовых координатах задается линейным урав­нением, а каждое линейное уравнение задает на плоскости прямую.

Напомним, что линейным уравнением (относительно пере­менных x и у) называется уравнение вида

Ах + By + C = 0, (13.1)

в котором коэффициенты A, В не равны нулю одновременно, т. е. пара (А, В) (0, 0).

Чтобы написать уравнение прямой l, ее надо задать. Существуют разные способы задания прямой, что приводит к различным по форме уравнениям, которые, конечно, равносильны, так как имеют одно и то же множество решений — координаты точек прямой l.

Общее уравнение прямой на плоскости.

	рис. 13.1

Пусть на плоскости введена декартова система координат Oxy и пусть l — некоторая прямая. Фиксируем на l какую-нибудь точку с координатами и какой-нибудь ненулевой вектор N, перпендикулярный прямой l (рис.13.1). Ясно, что заданием точки и вектора N прямая l определяется однозначно. Пусть вектор N имеет координаты (A, В), т. е. N = Ai + Bj, где i, j —единичные векторы вдоль осей x и у. Очевидно, что точка М(x,y) принадлежит прямой l тогда и только тогда, когда , т. е. когда выполняется равенство = 0. За­писывая это равенство в координатах, получим уравнение прямой l, проходящей через точку и перпендикуляр­ной вектору N = Ai + Bj

А (х-х₀) + B(у-у₀) = 0. (13.2)

Это уравнение линейное. Таким обра­зом, доказана

Теорема 13.1. Всякая прямая на плоскости задается линейным уравнением.

Вектор, перпендикулярный прямой, называется нормальным вектором прямой. Уравнение (13.1) не зависит от выбора нор­мального вектора, поскольку все векторы, перпендикулярные l, коллинеарны и их координаты пропорциональны.

Теорема13.2. Всякое уравнение первой степени Ax + By + С = 0 задает на плоскости с декартовыми коорди­натами x, у некоторую прямую, перпендикулярную векто­ру N= Ai + Bj.

□ Так как хотя бы один из коэффициен­тов A, В отличен от нуля, то уравнение (13.1) имеет бесконечно много решений. Выберем произвольно одно из них — . Тогда

Ах₀ + Ву₀ + С = 0. (13.3)

Вычитая почленно (13.3) из (13.1), получим уравнение

А (х-х₀) + B(у-у₀) = 0, (13.4)

равносильное уравнению (13.1). Как уже доказано, уравнение (13.2) задает прямую l, проходящую через точку , перпендикулярную вектору N = Ai + Bj. Так как уравнения (13.1) и (13.4) равносильны, т. е. имеют одно и то же множество решений, то уравнение (13.1) задает прямую l.

Уравнение (13.1) называется общим уравнением прямой.

Пример 2. Дана прямая 3x - у + 4 = 0. Написать уравнение прямой, прохо­дящей через точку (-1, 2) параллельно данной прямой.

Из теоремы 13.2 следует, что вектор v = (3, -1) перпен­дикулярен данной прямой. Так как данная и искомая прямые параллельны, то вектор v = (3, -1) перпендикулярен искомой прямой. Тогда прямая, параллельная данной, имеет уравнение 3(х+1)-(у-2) = 0 или 3х – у + 5 = 0.

Пример 3. Даны вершины треугольника A(1, -1), В(-2, 1), С(2, 4). Написать уравнение высоты AD, опущенной из вершины A на сторону ВС.

Решение. Высота AD перпендикулярна вектору ВС = (4, 3) и проходит через A(1, -1), и согласно теореме 13.1 ее уравнение име­ет вид 4(x - 1) + 3(у + 1) = 0 или 4х + 3у - 1 = 0.

Уравнение прямой с угловым коэффициентом.

Об­щим уравнением задается прямая при любом ее расположении относительно осей координат. Рассмотрим теперь прямые, не параллельные оси Oу. Для таких прямых удобно пользоваться так называемым уравнением с угловым коэффициентом.

Пусть l — прямая, не параллельная оси Oу, заданная общим уравнением

Ах + By + С = 0 (13.5)

Так как l D Oу, то В ­ 0, и, следовательно, уравнение (13.5) можно переписать в виде

Ax + By + C = 0 (13.6)

где - угловой коэффициент прямой l, - свободный член.

Коэффициенты в этом уравнении имеют «наглядный смысл». Ясно, что коэффициент b есть ордината точки пересечения прямой l с осью Oу. Выясним геометрический смысл k.

Пусть l пересекает ось Ox в некоторой точке P. Эта точка разбивает прямую l на два луча, один из которых Г лежит в полуплоскости у > 0. Углом между прямой l и осью Ox назовем угол между лучом Г и положительным направлением оси Ox. Тогда угловой коэффициент равен тангенсу угла k = tg . Если l параллельна оси Ox или совпадает с ней, то естественно считать, что = 0.

Еще раз отметим, что уравнение (13.6) вводится лишь для прямых, не параллельных оси Oy (иначе k = 4).

Век­торное уравнение прямой.

Пусть дана какая-нибудь точка и вектор 0, который считаем приложенным к точке :

=

Эти данные определяют прямую l как геометрическое место концов всевозможных векторов вида

= t , (13.7)

где t пробегает все вещественные числовые значения. Вектор = , очевидно, является направляющим вектором прямой. Можно сказать, что наша прямая есть геометрическое место всех точек М, удовлетворяющих уравнению (13.7), а само это уравнение можно назвать уравнением прямой в векторной форме (или век­торным уравнением прямой). Ясно, что каждая прямая может быть задана, таким образом, какой-нибудь своей точкой и на­правляющим вектором = . Существенным преимуществом уравнения (13.7) является то, что оно позволяет задать прямую не только на плоскости, но и в пространстве.

Параметрическое уравнение прямой

Записав векторное уравнение прямой в координатах, мы получим ее параметрическое уравнение. На плоскости оно имеет вид

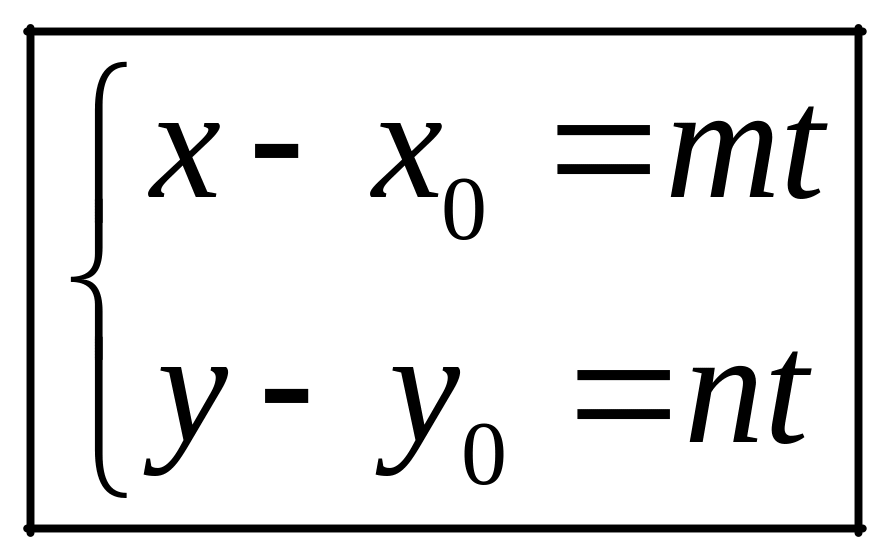, (13.8)

где , {а, b} — координаты направляющего вектора = .

Пример 4. Написать параметрическое уравнение прямой 2х + у — 1 = 0. Полагаем x = t. Из уравнения данной прямой находим у = 1 — 2х. На­конец,

- параметрическое уравнение данной прямой, оно равносиль­но данному уравнению.

Пример 5. Написать общее уравнение прямой .

Исключая параметр t из системы, получим общее уравнение данной прямой -2x+y+5=0.

Каноническим уравнением прямой на плоскости

Система уравнений (13.8) равносильна одной пропорции

, (13.9)

называемой каноническим уравнением прямой на плоскости.

Уравнение прямой, проходящей через две заданные точки

Если прямая задана двумя своими точками и , то ее направляющий вектор = имеет координаты , и уравнение (13.9) превращается в

. (13.10)

Это и есть уравнение прямой, проходящей через две заданные точки = ( ) и = ( ).

Пример 13. Написать уравнение прямой l, проходящей через точки A(1,2) и B(-3,1).

Вектор АВ = (-4, -1) параллелен прямой l , а точка A(1, 2) принад­лежит этой прямой. Следовательно, каноническое уравнение пря­мой l имеет вид , а уравнение прямой, проходящей через две точки .