12.4 Смешанное произведение векторов

Смешанным произведением векторов , , называется скалярное произведение векторов и .

Свойства

1) ,

2) , .

3) модуль смешанного произведения некомпланарных векторов равно объему

параллелепипеда, построенного на этих векторах.

Замечание. Из этого свойства следует, что смешанное произведение

некомпланарных векторов не равно нулю.

4) - компланарные

5)

6)

		Рис. 4.5

□1. Пусть в ортонормированном базисе векторы имеют координаты , , . Тогда смешанное произведение можно представить в виде определителя

,

,

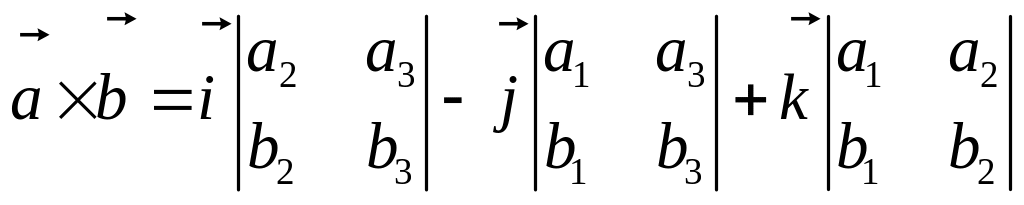
Следовательно, .

2. Истинность свойств 2, 4, 5, 6 следует из свойств определителя.

3. Из 1 свойства . Тогда .■

12.5 Коллинеарные векторы

Два ненулевых n-мерных вектора A и B называются коллинеарными, если угол между ними равен нулю или . Нулевой вектор будем считать коллинеарным любому вектору. Коллинеарные векторы обозначаются A B, неколлинеарные A B, сонаправленные - A B, противоположно направленные - А В.

Теорема 12.2 Для того, чтобы вектор А был коллинеарен ненулевому вектору В необходимо и достаточно, чтобы существовало такое число , чтобы А= В.

□ Необходимость. Пусть A B. Если A = = 0

Если A

Достаточность непосредственно следует из определения умножения вектора на число. ■

12.6 Разложение вектора по системе векторов

Пусть дана система m-мерных векторов . Выберем n про­извольных чисел, . Заметим, что чисел ровно столько, сколько векторов в системе.

Вектор называется линейной комбинацией векторов с коэффициентами .

Пусть теперь наряду с векторами дан еще n-мерный вектор В. Будем говорить, что вектор B линейно выражается через век­торы , если он равен некоторой линейной комбинации век­торов , т. е. найдется такой набор чисел , что

(12.4)

В этом случае будем говорить также, что вектор B разлагается по векторам . Числа в разложении (12.3) называются коэффициентами разложения вектора B по системе .

Разложение считается отличным от раз­ложения (12.3), если различна хотя бы одна пара соответствующих ко­эффициентов разложения (например, ).

Приведем несколько простых, но очень важных утверждений, в которых вопрос о разложении вектора B по системе ре­шается элементарно.

1. Нулевой вектор разлагается по каждой системе векторов .

.

12. Если вектор B разлагается по части системы векторов , то он разлагается и по всей системе векторов.

□ Предположим, для определенности, что часть системы совпадает с первыми k векторами , и пусть

, тогда ■

12. Каждый n-мерный вектор разлагается по диаго­нальной системе n-мерных векторов , ,…, .

= (1,0,0,..., 0),

= (0, 1,0,…0),

……………………

с коэффициентами, которые равны координатам вектора В.

□ . ■

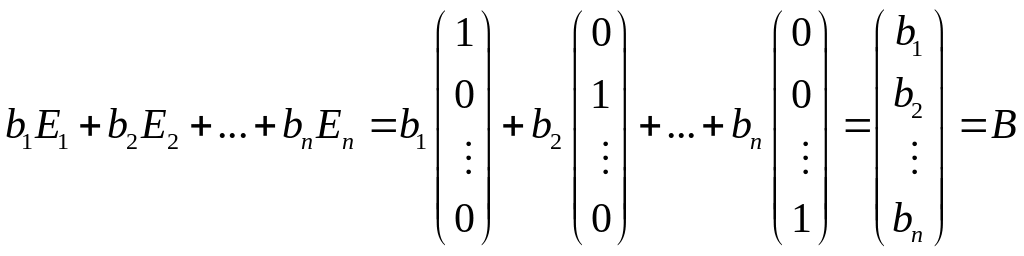12. Если вектор A разлагается по системе векторов , а каждый вектор этой системы разлагается по системе векторов , то вектор A разлагается по системе векторов .

□ Из условия следует, что

(12.6)

(12.7)

После подстановки соотношений (12.5) в равенство (12.4) получим

т. е. вектор A разлагается по системе векторов .■

Если вектор B и система - произвольные векторы, то задача разложения вектора B по системе , как будет пока­зано далее, сводится к решению системы линейных уравнений.