40. Правило Лопіталя- Бернуллі. Розкриття невизначеності 0/0 та ∞/∞ .

Пра́вило Лопіта́ля — у математичному аналізі — метод знаходження границь функції, розкриття невизначеностей вигляду і . Теорема, що обґрунтовує метод, стверджує що за деяких умов границя від частки функцій дорівнює границі частки їхніх похідних. Правило говорить, що якщо функції і задовольняють такі умови:

1. або ;

2. ;

3. в проколотому околі ;

4. Якщо і — диференційовані в проколотому околі ,

то існує . При цьому теорема вірна і для інших баз. Доведемо теорему для випадку, коли границі функцій дорівнюють нулю (т.з. невизначеність вигляду ). Оскільки ми розглядаємо функції і лише у правому проколотому півоколі точки , ми можемо неперервним чином їх довизначити в цій точці: нехай . Візьмемо деякий з даного півоколу і застосуємо до відрізку теорему Коші. За цією теоремою отримаємо:

,

але , тому .

Далі, записавши визначення границі функції відношення похідних і позначивши останню через , з отриманої рівності виводимо:

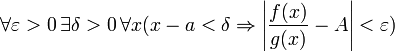для скінченної границі і

для нескінченої,

що є визначенням границі відношення функцій.

Відношення нескінченно великих Доведемо теорему для невизначеностей вигляду .

Нехай, для початку, границя відношення похідних скінченна і рівна . Тоді, при прямуванні до справа, це відношення можна записати як , де — O.

Запишемо цю умову:

.

Зафіксуємо з відрізка і застосуємо теорему Коші до всіх з відрізка :

, що можна привести до такого вигляду:

.

Для , достатньо близьких до , вираз має межу першого множника правої частини рівний одиниці (так як і — константи, а і прямують до безмежності). Значить, цей множник рівний , де — нескінченно мала функція при прямуванні до справа. Випишемо визначення цього факту, використовуючи те ж значення , що і в визначенні для :

.

Отримали, що відношення функцій можна подати у вигляді , і . По будь-якому данному можна знайти таке , щоб модуль різниці відношення функцій і був менше , значить, границя відношення функцій дійсно рівна .