1. Множини та дії над ними. Множина дійсних чисел.Множина – це сукупність об’єктів будь-якої природи які об’єднуються в цю сукупність за певною ознакою. Множина вважається заданою якщо задана характеристика її об’єктів за якою можна вказати чи цей об’єкт належить даній множині чи ні. Множини прийнято позначати великими буквами латинського алфавіту, а елементи – маленькими. А={1;2;3} – якщо множина має скінченну кількість об’єктів. А={1;2;3…} – якщо множина має нескінченну кількість об’єктів. Кажуть, що множина В – підмножина множини А (В міститься в А), якщо кожен елемент множини В є елементом множини А. Позначають . Символічний запис: . Порожня множина ø, яка зовсім не містить елементів, за означенням входить до числа підмножин довільної множини. Для довільної множини А сама множина А і порожня множина називаються невласними підмножинами. Всі решта підмножини називають власними. Об’єднанням двох множин А та В називають множину, яка складається із всіх елементів, що належать хоча б одній із цих множин. Записують так . Перетином двох множин А та В називають множину, яка складається із всіх елементів, що належать як одній, так і другій множині. Символічний запис: . Різницею двох множин А та В називається множина, яка складається із всіх елементів, що належать першій із них і не належать другій. Символічний запис: . Якщо , то різниця множин 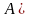називається доповненням множини В до множини А. Об’єднання різниць та називають симетричною різницею. Інколи множину, підмножини якої розглядаються в деякій задачі, називають універсальною для цієї задачі. Прямим або декартовим добутком множин А та В називається множина всіх упорядкованих пар (а,b) елементів, із яких перший належить першій множині А, а другий – другій множині В. Множина дійсних чисел. Дійсні числа — елементи певної числової системи, яка містить у собі раціональні числа і, в свою чергу, є підмножиною комплексних чисел. Дійсні числа виникли у в’язку з вимірюванням відрізків. Множина дійсних чисел складається з раціональних та ірраціональних чисел.

2. Властивості дійсних чисел. Модуль дійсного числа.Властивості дійсних чисел сформульовано у вигляді аксіом. Принцип Архімеда. Яким би не було число а існує ціле додатнє число n таке що n>=а. Для будь-яких чисел а і б має місце співвідношення тільки одне. Для будь-яких чисел а і б існує тільки одне число, яке є їх сумою. Існує число яке називається нуль. Існує число протилежне до а. Для будь-якої пари існує єдине число с яке називається добутком. Існує число яке ми називаємо 1 що а*1=а. Для кожного існує обернене яке позначають 1/а. Для будь-яких чисел а і б (б!=0) існує число , яке називають їхньою часткою. Модулем дійсного числа а називається невід’ємне число яке задовольняє умову |a|=a якщо a>=0, або -a якщо a<0.Геометричний зміст |a-b|- це відстань між точками А(а) та В(б). Яким би не було число а існує ціле додатнє число n таке що n>=а. Теорема Кантора множина всіх дійсних чисел з числового відрізка (0;1) є незліченною множиною.|a+b|<=|a|+|b|,|a-b|>=|a|-|b|,|a*b|=|a|*|b|.

3. Змінна величина , варіанта. Границя варіанти Змінну яка приймає деяку послідовність значень називають варіантою. Значення змінної може приймати навіть одне значення тому сталу величину можна вважати як частину змінної. Стале число а будемо називати границею варіанти Хn якщо для будь-якого Е>0 знайдеться такий номер який залежить тільки від вибору Е |Xn-a|<E. При цьому Е може бути як завгодно малим додатнім числом. Змінна Xn має границею число а якщо починаючи з якогось номера всі значення попадають у відрізок 2Е яким би це Е мале не було з центром в точці а.

4. Нескінченно малі та нескінченно великі величини. Змінну Xn називають нескінченно малою величиною, якщо усі члени цієї варіанти починаючи з деякого номера стають меншими від наперед заданого як завгодно малого числа. Змінну Xn називають нескінченно великою якщо усі члени цієї варіанти починаючи з деякого номера стають більшими від наперед заданого як завгодно великого додатного числа. Якщо не скін вел величина починаючи з якогось місця приймає тільки додатні знач то її границя є +нескінченість. Якщо нескін вел величина поч. з якогось місця приймає тільки від’ємні значення то її границя є –нескін. Якщо змінна Xn є не скін велика то 1/ Xn – не скін мала.

5. Найпростіші теореми про границю змінної.Якщо варіанта Xn має границею число а і а>p, то всі значення змінної починаючи з якогось номера також будуть більші за р. Якщо варіанта Xn має границею число а і а<p, то всі значення змінної починаючи з якогось номера також будуть менші за р. Якщо Xn має границею а і а більше 0, то всі знач змінної поч. з якогось номера також будуть більші 0. Якщо Xn має гран число а то вона обмежена. Якщо Xn має гран число а то ця границя єдина.

6. Граничний перехід в рівностях та нерівностях. Якщо при всіх значеннях n або починаючи з якогось місця виконується Xn= Уn і кожна із змінних має границю ліміт Xn=а,ліміт Уn=б то ці границі рівні (а=б).Якщо для всіх значень змінної Xn Уn, Zn чи починаючи з якогось місці виконується Xn<=Уn<= Zn і ліміт Xn=ліміт Zn=а, то Уn також має рівну границю ліміт Уn=а. Якщо в деякому проко- лотому околі точки х₀ і існують границі в т.х₀ то _.

7. Леми про нескінченно малі. Арифметичні дії над змінними. Сума будь-якої кількості нескін малих є нескінченно мала величина. |Xn-+Уn|<=|Xn|+|Уn| Добуток обмеженої величини на величину нескін малу є величина нескін мала. Якщо границі відношень нескінченно малих не існує то кажуть що такі не скін малі не порівнювані. Якщо Xn має скін гран а, а Уn – б то їх сума (а+б) також скінченна.Так само про добуток.І так само про частку.

9. Границя монотонної варіанти число е. Якщо варіанта монотонно зростаюча і обмежена зверху, то вона має скін гран. Якщо варіанта монотонно спадна і обмежена знизу то вона має скін границю. Число Ейлера ірраціональне, це неперіодичний, нескінченний дріб який приблизно дорівнює 2,71828…Число Ейлера є границею послідовності lim n-прямує до не скін.(1+1/n)в степені n=е. Число “е”, прийняте за основу системи логарифмів, прийнято називати натуральними. Натуральний логарифм х позначається символом ln x.

10. Лема про вкладені проміжки. [a;b],[a1;b1][an;bn] – сукупність відрізків, таких що a<=a1<=an, b<=b1<=bn – називають системою вкладених відрізків. Яка би не була послідовність вкладених відрізків завжди знайдеться таке число яке належить всім відрізкам. Будь-яка система вкладених відрізків для яких довжина прямує до 0 із зростанням номера n має тільки одне число, яке належить всім цим відрізкам.

11. Порівняння нескінченно малих. Еквівалентні нескінченно малі.Дві нескінченно малі альфа і бета будемо називати нескінченно алими однакового порядку якщо їхнє відношення при ліміт х->а альфа/бета і ліміт х->а бета/альфа

Має скінченну границю відмінну від 0.Якщо границя відношень нескін малих альфа і бета при х->а дорівнює 0 то кажуть що альфа нескін мала вищого порядку ніж бета і навпаки.При х->0 – нескін малі однакового порядку.Якщо границя відношень нескін малих не існує то кажуть що такі нескін малі не порівнювані.Нескінченно малі будемо називати еквівалентними при х->а якщо границя їхнього відношення =1.

12. Класифікація нескінченно великих. Якщо ліміт х->а y(x)/g(x)=00 то y(x)-нескін велика вищого порядку а g(x)-нескін велика нижчого порядку. Якщо ліміт х->а y(x)/g(x)до к степеню=б – скінченна то y(x) є нескінченно великою катого порядку по відношенню до g(x). Якщо границя відношень нескін великих не існує то кажуть що такі нескін великі не порівнювані. Якщо ліміт х->а y(x)/g(x)=с – скінченна то кажуть що ці нескінченно великі однакового пордяку.

13. Означення границі функції на мові послідовностей та на мові «ε-δ». Означення за Коші. Стале число А будемо наз гран функції f(x) при х прямуючому до а якщо для будь-якого Е>0 існує б>0 таке що |Х-а|<б випливає | f(x) -А|<Е. Означення за Гейне. Число А наз гран функції f(x) при х прямуючому до х0 якщо для будь-якої послідовності {Xn} такої що Хn != Х0 і lim n прямує до нескінченості Хn= Х0 відповідна послідовність {f(Хn) } прямує до А.

15. Властивості функцій , що мають границю. Якщо функція f(x) при х->а має границю А і А>р то всі значення змінної починаючи з якогось місця також будуть більші за р. так само для А менше р. Якщо функція f(x) маж границею а при х->а і g(x) має границею б при х->а то і сума f(x)+ g(x)=а+б.

16. Границя монотонної функції. Загальний критерій Больцано - Коші . Існування границі функцій в точці. Якщо функція монотонно зростаюча і необмежена то вона має границю +00.Якщо функція монотонно спадна і необмежена то вона має границю -00. Якщо функція монотонно зростаюча для значень х близьких до а (точка згущення) і обмежена зверху при х —> a то вона має скінченну границю. Якщо функція монотонноспадна для значень х близьких до а (точка згущення) і обмежена знизу при х —> a то вона має скінченну границю. Для того щоб фікція f(x) мала скінченну границю при х —> a необхідно й достатньо для щоб будь-якого Е>0 знайшовся такий номер N який залежить тільки від вибору Е тоді справджується рівність | f(x штріх) - f(x) |<Е. Число А називається границею функції f(x) в точці х0 при хх0 якщо для будь-якого E>0 можна знайти таке b>0,що при всіх х, які задовольняють нерівність <0|x-x0|<b, виконують нерівність |f(x) – A|<E.

17. Означення неперервності функції в точці. Дії над неперервними функціями. Функцію f(x) наз неперервною в точці а якщо границя функції = знач функції в цій точці лім еф від х=еф від а. Якщо функція неперервна в кожній точці деякого проміжку то вона неперервна на всьому проміжку. Функцію будемо наз неперервною в т а якщо яку б послідовність знач аргумента збіжну до а ми б не взяли то відповідна послідовність знач функції f(x) буде збіжна до f(а). Функцію f(x) будемо називати неперервною в т х=а якщо для будь-якого Е>0 знайдеться б>0 |Х-а|<б випливає | f(x) - f(а) |<Е. Сума, різниця, добуток і частка від ділення двох неперервних функцій також неперервна (для частки – за винятком тих значень аргументів, що перетворюють на нуль знаменник). f(x)* g(x), f(x)+ g(x), f(x)-g(x), f(x)/g(x),

18. Точки розриву та їх класифікація. Якщо границя функції f(x) в т х=а не існує або =00 або ця границя не рівна знач функції в цій точці то кажуть що функція f(x) в т х=а має розрив.Якщо границя існує то говорять про розрив типу стрибка.Якщо можна покласти f(а)=а і функція стане неперервною то кажуть про поправний розрив.Якщо границя функції в т х=а не існує або =00 то кажуть про розрив другого роду. Монотонно зростаюча(спадна) функція може мати розриви тільки першого роду.

19. Неперервність монотонної функції. Неперервність елементарних функцій. Якщо функція f(x) монотонно зростаюча на деякому проміжку Х і своїми значеннями заповнює даний проміжок повністю то вона на цьому проміжку неперервна.Монотонно зростаюча(спадна) функція може мати розриви тільки першого роду. Роздивившись графіки основних елементарних функцій, зауважимо, що вони всі неперервні на своїх областях визначення (лінії не розриваються в точках х є D_f). Тоді із означення елементарної функції і зауваження отримуємо важливу теорему.

Теорема. Елементарна функція є неперервною на своїй області визначення.

Основними елементарними функціями є степенева х в степені а показникові а в степені х логарифмічна тригонометрична оберненотригометрична.

20. Неперервність складеної функції . Застосування неперервності до обчислення границь. Функція у = F(u), де u = j(x), називається складною (складеною) функцією, або суперпозицією функцій F(u) та j(х), і позначається y = F(j (x)).Якщо j(x) неперервна в точці х=а а функція F(u) неперервна у відповідній точці j(а) то функція F(j(x)) – неперервна в точці х=а. Якщо f неперервна (наприклад елементарна), то можна заносити границю в аргумент: .Приклад. .

21.Перша і друга теорема Больцано-Коші. Якщо функція f(x)неперервна на замкненому відрізку [a;b] і на кінцях відрізка приймає різні по знаку значення f(а)* f(б)<0, тоді між а та б знайдеться т с така що f(с)=0 а<c<b. Друга теорема Больцано-Коші. Якщо функція f(x) визначена і неперервна на проміжку [a;b] і приймає різні значення f(а)=А f(б)=В то яке б не було число С, яке знаходиться А<С<В між А і В на проміжку [a;b] знайдеться т с а<c<b така що f(с)=с.

22. Існування оберненої функції. Якщо кожному елементу з множини У ставиться у відповідність тільки один елемент з множини Х то кажуть що задана обернена функція.ґ=Нехай функція f(x) визначена і строго монотонно зростає та неперервна на деякому проміжку Х тоді на відповідному проміжку У з множини значень функції існує обернена функція яка також є монотонно зростаючою і неперервною.

23. Перша і друга теорема Вейрштраса. Теорема Кантора та наслідок з неї. Якщо функція f(x) визначна і неперервна в замкнутому проміжку то вона на цьому проміжку обмежена. Друга теорема Вейєрштраса. Якщо функція f(x) визначна і неперервна в замкнутому проміжку то на цьому проміжку вона досягає свого найбільшого і найменшого значення. Теорема Кантора. Якщо функція f(x) визначена і неперервна в замкнутому проміжку то вона на цьому проміжку рівномірно неперервна.Наслідок Якщо функція f(x) визначена і неперервна на замкненому проміжку то для Е>0 знайдеться б>0 таке що якщо цей проміжок розбити на відрізки менші з б то коливання функції на кожному з них буде менше за Е.

24. Задачі , які приводять до поняття похідної. Означення похідної. Геометричний зміст похідної визначає кутовий коефіцієнт дотичної , а швидкість виражає фізичний зміст похідної.Можна похідну від функції в точці розглядати як швидкість зміни функції в цій точці. Похідною функції f(x) у точці х0 називається границя (якщо вона існує) відношення приросту функції у точці х0 до приросту аргументу Δх, якщо приріст аргументу прямує до нуля і позначається f'(x0).

25. Похідна оберненої функції. Похідні основних елементарних функцій. Похідні основних елементарних функцій

Похідна оберненої функції

Похідна елементарної функції є також елементарною функцією.

26. Формули для приросту функції. Зв’язок з диференційованістю і неперервністю функції. f(б)- f(а)= f'(с) (б-а), хє(а,б) х+дельта х є(а,б), f(х+дельта х)!= f(х) звідси отримуємо формулу скінченних приростів. f(х+дельта х)- f(х)= f'(с)*дельта х. Якщо функція у = f(x) диференційована в деякій точці х0, то вона в цій точці неперервна. 3 цієї теореми випливае, що неперервність функції є необхідною умовою диференційованості функції. Це означае, що в точках розриву функція немає похідної, тобто вона не диференційована.

28. Односторонні та нескінченні функції. Якщо т Х0 є лівим чи правим кінцем відрізка то говорячи про похідну як про границю відношення приросту функції до приросту аргументу матимемо на увазі що в першому випадку приріст аргумента має бути додатнім а в другому від’ємним.Тобто буде йти мова про односторонні похідні.Якщо границя відношення приросту функції до приросту аргументу існує але рівна 00 в такому випадку говорять про нескінченні похідні.В такому випадку дотична до кривої вертикальна.

29. Основні теореми диференціального числення(Ферма, Дарбу, Ролля, Лагранжа, Коші). Ферма. Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку. Якщо вона досягає свого найбільшого чи найменшого значення в якійсь точці х=с є(а,б) то похідна в цій точці =0 f'(с)=0.Дарбу. Якщо деяка функція на замкнутому відрізку є похідною іншої функції, то на цьому відрізку вона набуває усіх проміжних значень між значеннями на краях відрізка.Ролля Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку. На кінцях проміжку приймає однакові значення f(а)= f(б) тоді знайдеться т с яка є (а,б) що f'(с)=0. Лагранжа. Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку.На кінцях проміжку приймає не рівні значення f(а)=А ,f(б)=В А!=В тоді знайдеться внутрішня точка сє(а,б)така що має місце рівність (f(б)- f(а))/б-а= f'(с). Коші. Нехай функція f(x) визначена і неперервна на даному проміжку (а,б) має похідну хоча би у відкритому проміжку при чому g’(x)!=0 хє (а,б) тоді знайдеться така точка с є (а,б) що (f(б)- f(а))/ (g(б)- g(а))= f'(с)/ g’(с). Доведення Лагранжа.Розглянемо на проміжку [a;b] наступну функцію:

Перевіримо, що для функції F[x] виконані всі умови теореми Ролля. І справді, F[x] неперервна на проміжку [a;b] та в усіх внутрішніх точках проміжка [a;b] має похідну: З формули (1) очевидно, що Згідно з теоремою Ролля на проміжку (а,б) знайдеться точка с така, що З рівності (2) витікає формула Лагранжа.

30 Означення диференціала

Нехай функція у = f (х) диференційовна в інтервалі (а, b), х (а, b).

Згідно з означенням похідної функції у = f (х) маємо

Змінна величина відрізняється від своєї границі на не­скінченно малу , тому

Функція диференційовна в точці х, тому вона неперервна в цій точці, але тоді при величини будуть нескінченно малими. Порядок малості цих трьох величин різний: мають однаковий порядок малості, а величина є нескінченно малою вищого порядку малості. Отже, при перший доданок у правій частині рівності (8) є головною части­ною приросту функції. Він є лінійним відносно .

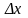(Означення 3.3. Якщо функція   має похідну   в точці  , то вираз   називається диференціалом (differential) функції в цій точці і позначається символом  . ) 

Означення. Головну лінійну частину приросту функції нази­вають диференціалом цієї функції. Диференціал функції у = f (х) позначають dy або df(x). Таким чином,

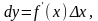
тобто для знаходження диференціала функції у = f (х), що має похідну в точці х, треба помножити значення цієї похідної на приріст аргумента або на dx ( = dx).

З рівності

(9)

одержимо, , тобто похідна функції дорівнює відношенню диференціала функції до диференціала незалежної змінної.

Диференціали часто застосовують для знаходження наближених значень функції.

Основні правила диференціювання.

Теорема 1. Похідна сталої дорівнює нулю.

y = c, то y΄ = 0

Теорема 2. Похідна алгебраїчної суми скінченого числа диференційованих функцій дорівнює алгебраїчній сумі похідних цих функцій

 Теорема 3 Похідна добутку двох диференційованих функцій дорівнює добутку першого множника на похідну другого плюс добуток другого множника на похідну першого:

Теорема 4 Сталий множник виносимо за знак похідної

 

(cu)΄ = cu΄, де c = const

Теорема 5 Якщо чисельник і знаменник дробу диференційовані функції (знаменник не перетворюється в нуль), то похідна дробу також дорівнює дробу, чисельник якого є різниця добутків знаменника на похідну чисельника і чисельника на похідну знаменника, а знаменник є квадрат знаменника початкового дробу

 

 

 

Зауваження: Похідна від функції,            де с = const:

 

Похідні від основних елементарних функцій.

Наприклад:

1.     

31 Інваріантність форми диференціалу першого порядку

Для диференційовної функції     , причому   для незалежної змінної  .

Нехай функції   та   - диференційовні і задають складну функцію  . Тоді  , але  . Тому  , де   - диференціал функції  .

Отже, диференціал першого порядку зберігає свою форму, тобто диференціал першого порядку має один і той же вигляд, який не залежить від того чи   - незалежна змінна чи функція.

На основі цієї властивості маємо наступні правила для обчислення диференціалу першого порядку:

1)  ;

2)  ;

3)  .

_____________________________________________________________

32 Застосування диференціала в наближених обчисленнях

З означення похідної функції в точці   випливає, що її приріст   можна подати у вигляді:  , де  , якщо  .

Отже, при малих   має місце наближена рівність:

 

, тобто  .

Звідки

.                (3.12)

 

Формула (3.12) дозволяє знаходити значення функції   в точці  , якщо відомі значення   і  , з точністю 

 

,

де  .

Приклад 3.13. Наближено обчислити значення  .

Розв’язання. В даному випадку  ,  . Покладемо  , що відповідає   в градусній мірі;

.

 

За формулою (3.12), отримаємо:

 

,

 

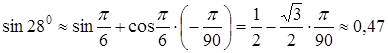тобто  .

Для того, щоб оцінити абсолютну і відносну похибки, скористаємось більш точним значенням, отриманим за допомогою калькулятора:  . Тоді  , а відносна похибка   дорівнюватиме:

.

 

Приклад 3.14. Наближено обчислити значення  .

Розв’язання. В даному випадку  .

 

Нехай  ,  , тоді   і за формулою (3.12):  , отримаємо, що:

 

.

 

Використовуючи калькулятор, отримаємо:  . Тоді  , а відносна похибка   дорівнюватиме: