2.3.2. Имитационное моделирование процесса обучения воспроизведению образов

Важной характеристикой обучаемых систем управления является их способность решать задачи воспроизведения образов. Задача воспроизведения образа заключается в том, что в каждый момент времени уже воспроизведенная часть образа является ситуацией, которая заставляет объект управления продолжать воспроизведение остальной части образа [83]. Полностью воспроизведенный образ является целевой ситуацией в этой задаче. К таким задачам воспроизведения образа можно отнести покраску, написание знаков, изготовление деталей из заготовок и т.д.

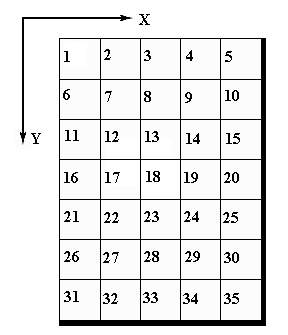Рис.2.19. Сетчатка технического глаза

Допустим, технический глаз имеет сетчатку 5х7 рецепторов. В зависимости от степени затемнения рецептора величина возбуждения может изменяться от 0 до 100. Пронумеруем рецепторы в соответствии с рис.2.19. Для обучения используем восемь опорных (рис.2.20, а, б, в, г, д, е, ж, з) и одну целевую ситуации (рис.2.20, и). Образы этих ситуаций характеризуются наборами чисел, отражающих степень затемнения рецепторов, и расположенных в порядке нумерации рецепторов. В качестве примера решения задачи обучения воспроизведению образа рассмотрим вычислительную модель воспроизведения изображения цифры “8”. Обучение проведем отдельно по каждой из осей координат. Сигналы управления в ситуациях обучаемой выборки зададим таким образом, чтобы результирующее движение исполнительного органа (например руки робота с краскопультом) было направлено по траектории написания цифры “8”. Заданную точность обучения в ситуациях выборки примем равной  0,1 ед.

Рис.2.20. Образы обучаемой выборки для обучения воспроизведению цифры “8”

Значения возбуждений рецепторов, расположенные построчно, образуют образы ситуаций обучаемой выборки:

Образы ситуаций обучаемой выборки: ______________________________________________________________________________Сигналы _________________ ____________________________________________________________________________________________управления: Опорные ситуации:_______________________________________________________________________________________________E_X__E_Y

1)_0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_79__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______10__–10 ; 2)_0__0__0__0__0_30_35__0__0__0_25_80_20__0__0__0_30_84__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_______0__–10 ; 3)_5_60_85__0__0_37_60__2__0__0_25_80_20__0__0__0_30_84__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______10____0 ; 4)_5_60_98_60__5_37_60__4_55_37_25_80_20__5__5__0_30_84__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_______0___10 ; 5)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_30_89_30__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_____–10___10 ; 6)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_95_30__0_25_80_20__0__0_30_35__0__0__0__0__0__0__0__0_______0___10 ; 7)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_95_30__0_25_80_20__0__0_37_60__2__0__0__5_60_85__0__0______10____0 ; 8)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_95_30__0_25_80_20__5__5_37_60__4_55_37__5_60_98_60__5_______0__–10 .

Целевая ситуация: 9)_5_60_98_60__5_37_60__4_60_38_25_80_38_80_25__0_50_100_50_0_25_80_38_80_25_37_60__4_60_38__5_60_98_60__5_______0____0 .

В результате расчета по алгоритму обучения получили следующие весовые коэффициенты:

по оси X: ___1) _0,004553; ___2) _0,054633; ___3) _0,061531; ___4) –0,073227; ___5) –0,006102; ___6) _0,033779; ___7) _0,054736; ___8) –0,000620; ___9) –0,073307; __10) –0,046393; __11) _0,022837; __12) _0,073080; __13) –0,003988; __14) –0,098842; __15) –0,030833; __16) _0,000000; __17) _0,045960; __18) –0,127815; __19) –0,030965; __20) _0,000000; __21) _0,023194; __22) _0,074220; __23) _0,024073; __24) _0,016237; __25) –0,000623; __26) _0,034086; __27) _0,054805; __28) –0,000915; __29) –0,072762; __30) –0,049674; __31) _0,004467; __32) _0,053600; __33) _0,058373; __34) –0,081049; __35) –0,006754;

по оси Y: ___1) _0,003798; ___2) _0,045577; ___3) _0,079047; ___4) _0,066830; ___5) _0,005569; ___6) _0,004934; ___7) _0,018544; ___8) _0,003747; ___9) _0,060418; __10) _0,041043; __11) –0,000319; __12) –0,001021; __13) –0,003290; __14) –0,007076; __15) _0,002197; __16) _0,000000; __17) _0,001678; __18) –0,126559; __19) _0,029360; __20) _0,000000; __21) _0,002576; __22) _0,008244; __23) _0,033037; __24) _0,122757; __25) _0,028106; __26) –0,002304; __27) –0,015663; __28) –0,004066; __29) –0,060829; __30) –0,044989; __31) –0,003854; __32) –0,046246; __33) –0,081927; __34) –0,075746; __35) –0,006312.

Теперь, если поместить в начало траектории рабочий орган, то сумма весовых коэффициентов, помноженных на соответствующие возбуждения рецепторов, будет определять сигнал управления движением по отдельной координате. Перемещаясь одновременно по двум координатам, исполнительный орган будет формировать изображение, которое в свою очередь будет изменять сигналы управления двигателями в соответствии с проведенным обучением. Таким образом воспроизводится изображение цифры “8”. Похоже на то, как знаменитый Мюнхаузен сам себя вытаскивал за волосы из болота.

Процесс воспроизведения изображения цифры “8” был смоделирован на персональном компьютере. Методика моделирования заключалась в следующем. Участок экрана монитора размером 200х280 пикселей белого цвета разбиваем на 35 ячеек размером 40х40 пикселей. Задаем начальное положение черного круга радиусом 20 пикселей в центре участка. Далее следует циклический опрос ячеек. На каждом цикле считается число пикселей черного цвета в каждой ячейке, которое делится на 1600 (общее число пикселей ячейки) и умножается на 100. Получаем степень затемнения отдельной ячейки. Умножаем ее на весовой коэффициент данной ячейки для оси X. Сложив полученные данные для всех ячеек, получаем управляющий сигнал перемещения центра черного круга по оси X. Аналогично получаем управляющий сигнал перемещения центра черного круга по оси Y. Наконец перемещаем центр круга по осям X и Y пропорционально полученным управляющим сигналам и переходим к следующему циклу опроса ячеек с учетом уже полученного затемнения ячеек. И так – многократно, пока не закончится воспроизведение образа. Все положения черного круга в ходе воспроизведения дадут стробоскопию его движения (рис.2.21).

Рис.2.21. Стробоскопия воспроизведения изображения цифры “8”

На стробоскопии хорошо видно, как при приближении к целевой ситуации (завершении воспроизведения) уменьшается скорость движения центра черного круга и при достижении цели становится равной нулю. Это – пример того, как компьютер был обучен именно писать заданный символ, а не извлекать заложенное в память компьютера изображение. Правильность воспроизведения изображения цифры “8” можно улучшить увеличив число промежуточных ситуаций обучаемой выборки. Следует обратить внимание на то, что никакого образа цифры “8” не хранится в памяти компьютера, не задана и траектория движения темного круга. Примерно также мы заучиваем и воспроизводим, скажем, стихотворение, когда каждая произнесенная строка вызывает собой следующую. В том, что это так, можно убедиться, попробовав рассказать казалось бы хорошо выученное стихотворение в обратном порядке, начиная с последней строки и заканчивая первой. Работа обучаемых систем управления в зависимости от окружающей ситуации определяет их удивительное свойство, которое заключается в компенсации погрешностей работы одного исполнительного двигателя работой других. На рис.2.22 показаны стробоскопии воспроизведения изображения цифры “8” с искажением управляющих сигналов перемещения по оси x (рис.2.22, а) в 1,2 раза и по оси y (рис.2.22, б) в 1,5 раза. Как видим, такое значительное искажение управляющих сигналов приводит к довольно незначительному искажению воспроизведенного образа.

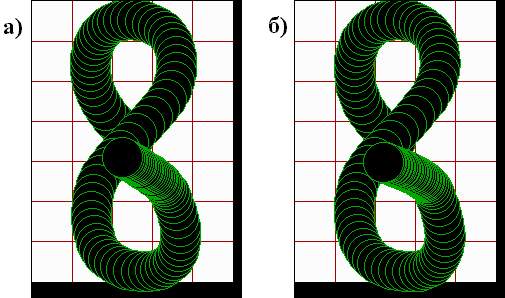Рис.2.22. Стробоскопия воспроизведения изображения цифры “8” а) сигналы по оси x в 1,2 раза меньше расчетных; б) сигналы по оси y в 1,5 раза меньше расчетных

Такая компенсация погрешностей управляющих сигналов происходит потому, что управляющие сигналы по осям формирует уже воспроизведенная часть заданного образа, и отклонение этой части от заданных параметров изменяет управляющие сигналы таким образом, что траектория воспроизведения восстанавливается. Воспроизведение изображения цифры “8” интересно тем, что в зависимости от уже воспроизведенной части образа траектория движения в средней точке (точке симметрии) имеет три различных направления.

Рассмотрим обучение воспроизведению несимметричного изображения цифры “2”.

Образы ситуаций обучаемой выборки: _______________________________________________________________________________Сигналы ________________________________________________________________________________________________________\______управления: Опорные ситуации(рис.2.23,а,б,в,г,д,е,ж,и,з):____ ______________________________________________________________________E_X__E_Y

1)_0__0__0__0__0__0__0__0__0__0__0_78__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______–10__–10; 2)_3__5__0__0__0_40_50__0__0__0_15_85__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0________5__–10; 3)_7_75_85__0__0_40_65__1__0__0_15_85__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0_______10____0; 4)_7_75_98_75__7_40_65__2_55_35_15_85__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0________0___10; 5)_7_75_98_75__7_40_65__2_60_40_15_85__0_70_25__0__0__0_10__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0__0______–10___15; 6)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_47_65__0__0__0_20__5__0__0__0__0__0__0__0__0__0__0__0______–10___15; 7)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__6_90_25__0__0_10_30__0__0__0_______–5___10; 8)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__7_90_25__0__0_40_50__0__0__0_______20____0; 9)_7_75_98_75__7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__7_90_25__0__0_40_100_80_0__0_______20____0.

Целевая ситуация (рис.2.23,к): 10)_7_75_98_75_7_40_65__2_60_40_15_85__2_75_25__0__0_50_65__0__0_30_85__5__0__7_90_25_0_0_40_100_100_100_40_______0____0.

В результате расчета по алгоритму обучения получили следующие весовые коэффициенты:

по оси X: ___1) _0,011381; ___2) _0,029500; ___3) _0,001939; ___4) –0,070359; ___5) –0,006567; ___6) _0,142883; ___7) _0,181098; ___8) –0,000772; ___9) –0,060293; __10) –0,041530; __11) _0,053581; __12) –0,126725; __13) _0,000906; __14) –0,119481; __15) –0,043481; __16) _0,000000; __17) _0,000000; __18) _0,018941; __19) _0,007525; __20) _0,000000; __21) _0,000000; __22) –0,023518; __23) –0,041896; __24) _0,002265; __25) _0,000000; __26) _0,016455; __27) –0,070555; __28) –0,019599; __29) _0,000000; __30) _0,000000; __31) _0,626929; __32) _0,300566; __33) –0,186764; __34) –0,141061; __35) –0,056424;

по оси Y: ___1) _0,002964; ___2) _0,051224; ___3) _0,073581; ___4) _0,066136; ___5) _0,006173; ___6) _0,000546; ___7) _0,011644; ___8) _0,001613; ___9) _0,052559; __10) _0,034923; __11) _0,000205; __12) –0,128136; __13) –0,000253; __14) _0,056207; __15) _0,020300; __16) _0,000000; __17) _0,000000; __18) –0,005709; __19) _0,001167; __20) _0,000000; __21) _0,000000; __22) _0,002324; __23) _0,002507; __24) –0,000632; __25) _0,000000; __26) –0,007867; __27) _0,006972; __28) _0,001937; __29) _0,000000; __30) _0,000000; __31) –0,249166; __32) –0,117595; __33) _0,072399; __34) –0,011669; __35) –0,004668.

Стробоскопия воспроизведения изображения цифры “2” представлена на рис.2.23,л.

Рис.2.23. Образы ситуаций обучаемой выборки и стробоскопия воспроизведения изображения цифры “2”

Если полученные весовые коэффициенты представить в виде оптических фильтров соответствующих участков сетчатки, степень затемнения каждого из которых пропорциональна значению его весового коэффициента, то получим негативы оптических преобразователей для воспроизведения цифр “8” (рис.2.24,а) и “2” (рис.2.24,б) в виде оптических фильтров.

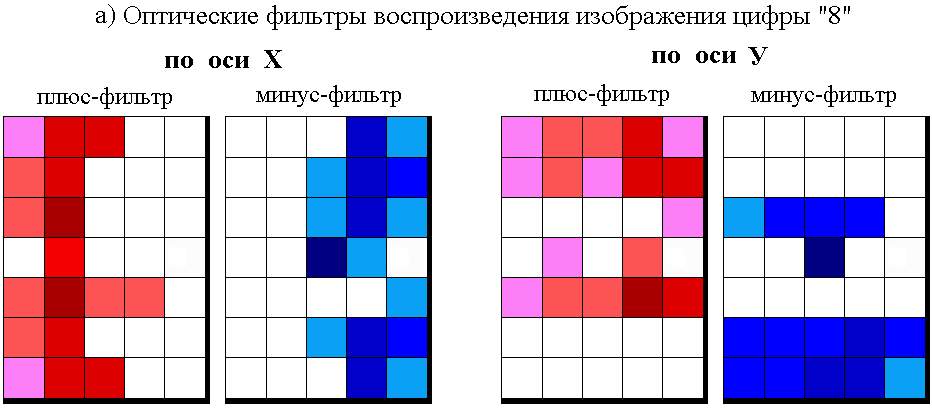
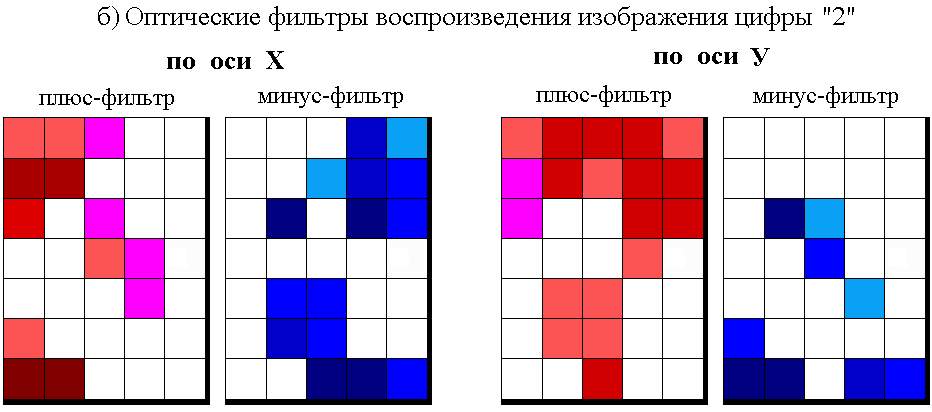Рис.2.24. Оптические фильтры воспроизведения а) цифры “8” б) цифры “2”

Как видно из рис.2.24, весовые коэффициенты обучаемой системы управления (резисторные или оптические) не содержат эталонов ситуаций обучаемой выборки, а отражают весь процесс обучения. Если данные оптические фильтры выполнить в виде позитивов, то они реально могут быть использованы в оптической обучаемой системе управления для воспроизведения цифр “8” и “2” (см.раздел 5.1). Из рисунка видно так же, как обучаемые системы управления решают проблему выделения так называемых значимых и незначимых признаков, весьма сложную для теории распознавания образов. Нет необходимости заранее определять степени значимости признаков (как это делается при распознавании образов), их значимость формируется автоматически в процессе обучения. Те рецепторы, весовые коэффициенты которых, сформированные в процессе обучения, имеют большее абсолютное значение – более значимы, и наоборот. Рецепторы, весовые коэффициенты которых равны нулю, воспринимают признаки, незначимые для решения данной задачи (рецепторы 16 и 20 – для воспроизведения образа цифры “8”; рецепторы 16, 17, 20, 21, 25, 29, 30 – для воспроизведения образа цифры “2”). Причем, наличие этих рецепторов, т.е. избыточность информации, никак не влияет на способность обучаемой системы выполнять поставленную задачу.