2.2.6. Влияние порядка предъявления ситуаций обучаемой выборки на продолжительность обучения

Анализ влияния порядка предъявления ситуаций на продолжительность обучения будем проводить с помощью вычислительной модели обучаемой системы управления. В качестве примера рассмотрим два варианта обучения для пяти ситуаций с десятью числовыми признаками (таблица 1).

Таблица 1

№ п/п	Ситуации обучаемой выборки										Сигналы управления E
	b1	b2	b3	b4	b5	b6	b7	b8	b9	b10
1 2 3 4 5	8____8____6____3____1____1____6____4____4____2 7____2____0____5____0____7____8____5____3____1 6____3____8____4____1____9____4____2____9____4 2____0____7____2____0____5____3____0____6____1 8____6____4____9____6____4____9____7____4____9										1 2 3 4 5

Допуск на значения сигналов управления:  _E =  0,1 .

Первый вариант обучения:

Порядок предъявления ситуаций – циклический. Число шагов обучения, необходимых для достижения заданной точности: 225. Значения полученных в результате обучения весовых коэффициентов признаков:

___ ___0,277424; __–0,398268; ___0,391117; ___0,294749; ___0,171608; ___ ___0,102080; ___0,475452; __–0,008366; ___0,034453; ___0,045794.

Полученные в результате обучения фактические выходные сигналы в ситуациях обучаемой выборки имеют следующие значения:

______E_f1=0,943592; ___E_f2=1,931619; ___E_f3=3,079798; ___E_f4=3,940933; ___E_f5=5,000000.

Процесс приближения фактических сигналов управления к заданным значениям по шагам обучения при циклическом предъявлении ситуаций представлен на рис.2.10.

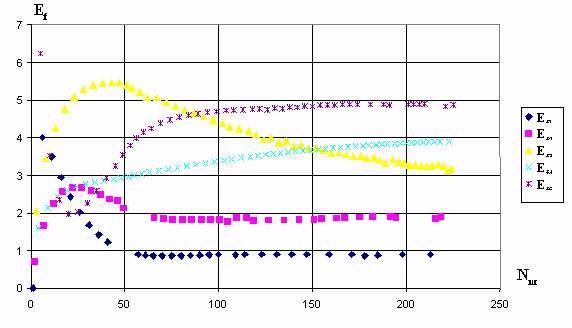Рис.2.10. Обучение при циклическом предъявлении ситуаций

Второй вариант обучения:

При этом варианте после каждого шага обучения определяются значения абсолютных ошибок для сигналов управления во всех ситуациях, и на следующем шаге предъявляют ситуацию, в которой ошибка сигнала управления была самой большой. Обучение до заданной точности закончилось за 153 шага. Значения весовых коэффициентов признаков, полученных в результате обучения:

______–0,269060; __–0,387141; ___0,392780; ___0,289534; ___0,166311; ______–0,105657; ___0,475572; __–0,007025; ___0,034779; ___0,039230.

Полученные в результате обучения фактические выходные сигналы в ситуациях обучаемой выборки имеют следующие значения:

______E_f1=1,079238; ___E_f2=1,963388; ___E_f3= 3,098165; ___E_f4=3,936747; ___E_f5=5,000000.

На рис.2.11 показан процесс приближения фактических сигналов управления к заданным значениям по шагам обучения для второго варианта предъявления ситуаций.

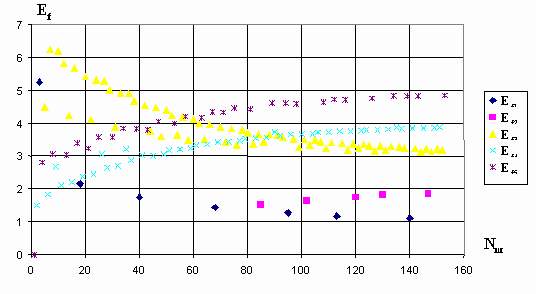Рис.2.11. Обучение с выбором на каждом шаге обучения ситуации с максимальной ошибкой выходного сигнала

Уменьшение числа шагов обучения при втором варианте обучения носит устойчивый характер, т.е. имеет место при любых образах и заданных выходных сигналах. Для данного примера число шагов, необходимых для достижения заданной точности при обучении по второму варианту, почти в полтора раза меньше, чем по первому варианту. Значения весовых коэффициентов признаков для двух вариантов близки и при уменьшении допуска на сигналы управления будут еще больше сближаться. Из приведенных графиков видно, как изменяются значения фактических сигналов управления по шагам обучения: на начальном этапе формируются сигналы управления, которые не соответствуют заданным значениям, затем значения сигналов приближаются к некоторой средней величине, и далее – расходятся, стремясь к заданным величинам до тех пор, пока не войдут в пределы допусков на сигналы управления. Рассмотренные варианты отражают реальные процессы обучения объектов, оснащенных обучаемыми системами управления. Так, при обучении робота обучатель может, используя метод “вождения за руку”, многократно циклически повторять движения робота в режиме обучения, добиваясь того, что робот будет двигаться с заданной точностью, необходимой для выполнения поставленной задачи. Таким образом реализуется первый вариант обучения. Того же результата обучатель может добиться, если по ходу движений робота будет подавать сигналы коррекции лишь в тех ситуациях, в которых сигналы управления исполнительными двигателями имеют наибольшие отклонения от требуемых значений, т.е. реализовывать второй вариант обучения, который позволяет значительно сократить его продолжительность. Алгоритм обучения, оптимизированный с точки зрения порядка предъявления образов ситуаций, представлен на рис.2.12:

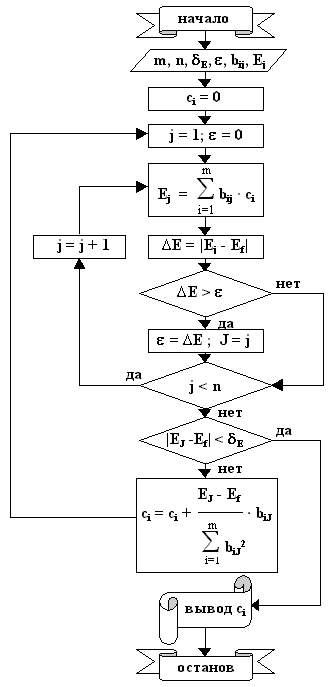Рис.2.12. Оптимизированный алгоритм расчета весовых коэффициентов